HDU 1568 Fibonacci【求斐波那契数的前4位/递推式】

Fibonacci

Time Limit: 1000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)

Problem Description

2007年到来了。经过2006年一年的修炼，数学神童zouyu终于把0到100000000的Fibonacci数列
(f[0]=0,f[1]=1;f[i] = f[i-1]+f[i-2](i>=2))的值全部给背了下来。
接下来，CodeStar决定要考考他，于是每问他一个数字，他就要把答案说出来，不过有的数字太长了。所以规定超过4位的只要说出前4位就可以了，可是CodeStar自己又记不住。于是他决定编写一个程序来测验zouyu说的是否正确。

 

Input

输入若干数字n(0 <= n <= 100000000)，每个数字一行。读到文件尾。

 

Output

输出f[n]的前4个数字（若不足4个数字，就全部输出）。

 

Sample Input

0
1
2
3
4
5
35
36
37
38
39
40

 

Sample Output

0
1
1
2
3
5
9227
1493
2415
3908
6324
1023

【分析】：

这是道神奇的题，求斐波那契数列的0到第100000000项的前四位，之前做过斐波那契数列的水题，求到63项

能用__int64解决，但是到100000000项的话用数组都会超时。

以下是大牛的解释：

先看对数的性质,loga(b^c)=c*loga(b),loga(b*c)=loga(b)+loga(c);
假设给出一个数10234432,那么log10(10234432)=log10(1.0234432*10^7)=log10(1.0234432)+7;

log10(1.0234432)就是log10(10234432)的小数部分.

log10(1.0234432)=0.010063744
10^0.010063744=1.023443198
那么要取几位就很明显了吧~
先取对数(对10取),然后得到结果的小数部分bit,pow(10.0,bit)以后如果答案还是<1000那么就一直乘10。
注意先处理了0~20项是为了方便。

这题要利用到数列的公式:an=(1/√5)
* [((1+√5)/2)^n-((1-√5)/2)^n](n=1,2,3.....)

log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0)+log10(1-((1-√5)/(1+√5))^n)

其中f=(sqrt(5.0)+1.0)/2.0;
因为log10(1-((1-√5)/(1+√5))^n)趋近于0
所以可以写成log10(an)=-0.5*log10(5.0)+((double)n)*log(f)/log(10.0);
最后取其小数部分。

而我们要取Fibonacci数的前4位，可以通过计算以10为底的对数，原理与HDU 1060 Leftmost Digit是一样的，不妨可以点开看看

另外，需要提及的一点是前20项Fibonacci数需要自己计算，一方面是因为Fibonacci数未满4位，更重要的一点是Fibonacci数较小时，公式的精确度不高

比如第17项Fibonacci应该是1597，但公式求得的是1596；而19项Fibonacci应该是4181，但公式求得的是4180

因此，我们需要先自己计算出Fibonacci数的前19项。

【代码】：

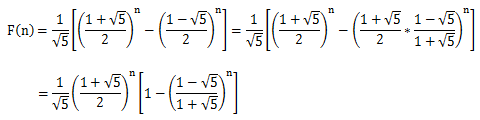
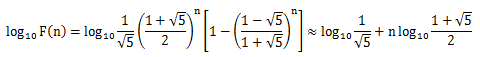
#include <bits/stdc++.h>
using namespace std;

typedef long long LL;
const int N = ;
const int inf = ;
const int mod = ;
int f[N];
int main()
{
    int n,i;
    double s;
    f[]=,f[]=;
    for(i=;i<N;i++)//由于接下来利用公式得出来的Fibonacci数不是精确的，越小的数则越不精确，所以前面一些Fibonacci数需要自己算
        f[i]=f[i-]+f[i-];
    while(~scanf("%d",&n))
    {
        if(n<N)
        {
            printf("%d\n",f[n]);
            continue;
        }
        s=log10(1.0/sqrt(5.0))+n*log10((+sqrt(5.0))/);  //调用公式
        s=s-(int)s;  //取小数部分
        s=pow(,s);
        while(s<)  //要求四位，所以要将小数点右边的数移到左边直到符合要求
            s*=;
        printf("%d\n",(int)s);
    }
    return ;
}  

数学、公式