SGU 149 树形DP Computer Network

　　这道题搜了一晚上的题解，外加自己想了半个早上，终于想得很透彻了。于是打算好好写一写这题题解，而且这种做法比网上大多数题解要简单而且代码也比较简洁。

　　首先要把题读懂，把输入读懂，这实际上是一颗有向树。第i(2≤i≤n)行的两个数u，d，其中u是i的父亲结点，d是距离。

　　第一遍DFS我们可以计算出以u为根的子树中，距离u最远的结点的距离d(u, 0)以及次远的距离d(u, 1)。而且，这两个不在u的同一棵子树中，如果u只有一个孩子，那么d(u, 1) = 0

　　第一遍DFS完以后，因为1是整棵树的跟，所以d(1, 0)就是距离1最远的距离。然后第二遍DFS，这次是用根的信息来更新它的子节点，此时d(u,0)d(u,1)的含义变为整棵树中距u最长和次长的距离。

　　如图：

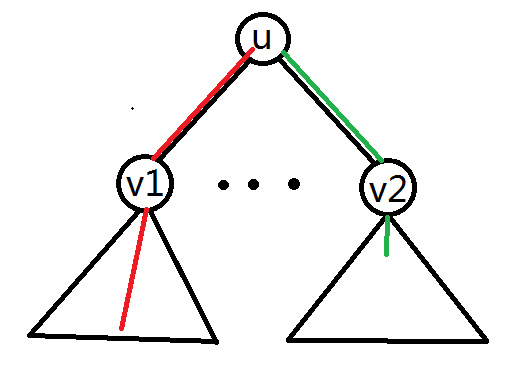
　　　　红线代表距u最长的距离，绿线是次长。因为最长距离在v1的子树中，所以就用dis(u, v1) + d(u, 1)(也就是那条绿线)来更新距v1的最长和次长距离；　　　　用dis(u, v2) + d(u, 0)(那条红线)来更新距v2的最长次长距离。

　　　　因此最终答案就是d(u, 0)

 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>
 using namespace std;

 const int maxn =  + ;
 vector<int> G[maxn], C[maxn];
 int n;

 int d[maxn][];

 void dfs(int u)
 {
     for(int i = ; i < G[u].size(); i++)
     {
         int v = G[u][i];
         dfs(v);
         int t = d[v][] + C[u][i];
         if(t > d[u][]) swap(t, d[u][]);
         if(t > d[u][]) swap(t, d[u][]);
     }
 }

 void dfs2(int u)
 {
     for(int i = ; i < G[u].size(); i++)
     {
         int v = G[u][i], t, w = C[u][i];
         if(d[v][] + w == d[u][]) t = w + d[u][];
         else t = w + d[u][];
         if(t > d[v][]) swap(t, d[v][]);
         if(t > d[v][]) swap(t, d[v][]);
         dfs2(v);
     }
 }

 int main()
 {
     scanf("%d", &n);
     for(int u = ; u <= n; u++)
     {
         int v, d; scanf("%d%d", &v, &d);
         G[v].push_back(u); C[v].push_back(d);
     }

     dfs();
     dfs2();

     for(int i = ; i <= n; i++) printf("%d\n", d[i][]);

     return ;
 }

代码君