2019ICPC陕西邀请赛复盘

题目链接：The 2019 ACM-ICPC China Shannxi Provincial Programming Contest

　　A：签到，按花费时间从小到大排个序

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 const int N=;
 int a[N];
 int main()
 {
     int n,t;
     while(~scanf("%d%d",&n,&t))
     {
         for(int i=;i<=n;i++)
             scanf("%d",&a[i]);
         sort(a+,a++n);
         int ans=;
         for(int i=;i<=n;i++)
         {
             if(t>=a[i])
             {
                 t-=a[i];
                 ans++;
             }
             else
                 break;
         }
         printf("%d\n",ans);
     }
     return ;
 } 

日常签到

　　L：签到，因为序列里的数都不一样，所以答案只跟n有关，两次同样的操作的话序列就换回来了，所以肯定是两个操作交替进行，然后照着题意打表找规律，注意1和3要特判

 #include<cstdio>
 int main()
 {
     int n,x;
     while(~scanf("%d",&n))
     {
         for(int i=;i<n;i++)
             scanf("%d",&x);
         if(n==)
             printf("1\n");
         else if(n==)
             printf("6\n");
         else if(n%==)
             printf("4\n");
         else if(n%==)
             printf("%d\n",*n);
         else if(n%==)
             printf("%d\n",n);
         else
             printf("12\n");
     }
     return ;
 }

日常打表

　　M：二分最短路，首先题意是，给出了一个星系里每个星球的路线图，然后有一艘飞船，它有三个属性，等级和最长的航行距离以及航行次数，初始都是0，然后可以升级，每升一级，花费费用c，最长航行距离增长d，航行次数增加e。如果某条路线的长度大于飞船的最长的航行距离，那么飞船不能走这条路线，并且每走一过一条路就消耗1的航行次数，当航行次数为0，飞船也不能走了。问从1号星球到n号星球的最小费用是多少。

　　我们就二分升级的次数，那么能走的路线就是长度小于等于次数*d的，在这个限制以每条路线距离为1，求一个1号星球到n号星球的最短距离，判断一下这个距离是不是小于等于次数*e。

 #include<cstdio>
 #include<queue>
 using namespace std;
 typedef long long ll;
 const int N=,inf=;
 struct Side{
     int v,ne,w;
     Side(){}
     Side(int v,int w):v(v),w(w){}
     bool operator< (const Side &s1)const{
         return w>s1.w;
     }
 }S[N<<];
 int sn,head[N],dis[N],vis[N];
 void init(int n)
 {
     sn=;
     for(int i=;i<=n;i++)
         head[i]=-;
 }
 void add(int u,int v,int w)
 {
     S[sn].v=v;
     S[sn].w=w;
     S[sn].ne=head[u];
     head[u]=sn++;
 }
 bool dijk(int n,ll lim,ll num)
 {
     priority_queue<Side> q;
     for(int i=;i<=n;i++)
     {
         vis[i]=;
         dis[i]=inf;
     }
     dis[]=;
     q.push(Side(,));
     int u,v;
     while(!q.empty())
     {
         u=q.top().v;
         q.pop();
         if(u==n)
             break;
         if(vis[u])
             continue;
         vis[u]=;
         for(int i=head[u];~i;i=S[i].ne)
         {
             v=S[i].v;
             if(S[i].w<=lim&&dis[v]>dis[u]+)
             {
                 dis[v]=dis[u]+;
                 q.push(Side(v,dis[v]));
             }
         }
     }
     return dis[n]<=num;
 }
 int main()
 {
     int n,m,c,d,e,u,v,w;
     while(~scanf("%d%d",&n,&m))
     {
         init(n);
         scanf("%d%d%d",&c,&d,&e);
         while(m--)
         {
             scanf("%d%d%d",&u,&v,&w);
             add(u,v,w);
             add(v,u,w);
         }
         int l=,r=1e5,mid,ans=-;
         while(l<=r)
         {
             mid=(l+r)>>;
             if(dijk(n,1ll*mid*d,1ll*mid*e))
                 r=mid-,ans=mid;
             else
                 l=mid+;
         }
         if(ans==-)
             printf("-1\n");
         else
             printf("%lld\n",1ll*ans*c);
     }
     return ;
 }

日常二分

　　C:计算几何。根据题意大概就是下面这个美美的图。

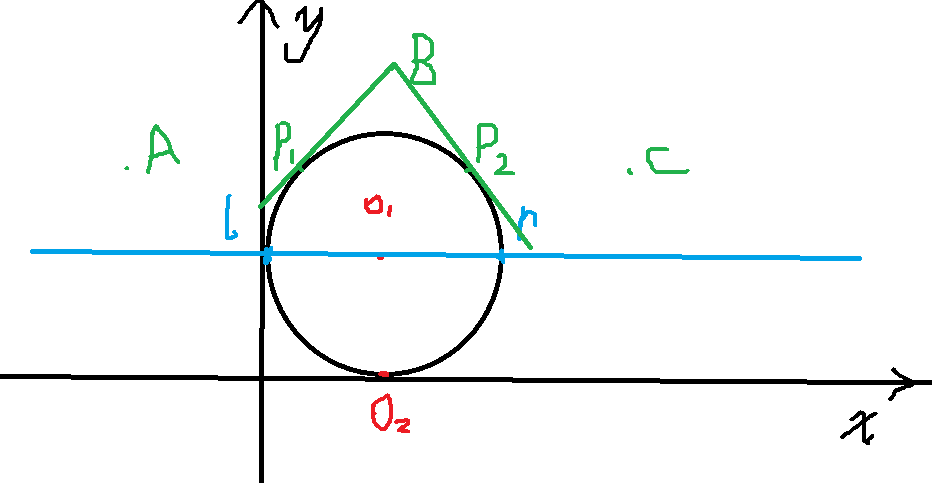
　　蓝色的线以下除了圆弧外都不能走，所以O₂肯定是先走4分之一圆弧，走到l或者r点处，然后如果目标点是A或者C的话，接下来肯定就是l与A的两点之间的距离，或者r与C两点之间的距离，而如果目标点是B点的话，那么就是得先求出两个切点p1,p2了，然后l或r走到p1或p2，最后再是p1或p2走到B的最短距离，求切点就是模板了。

 #include<cstdio>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 const double pi=acos(-1.0);
 struct Point{
     double x,y;
     Point(){}
     Point(double x,double y):x(x),y(y){}
 }pr,pa;
 double r;
 double dis(Point p1,Point p2){
     return sqrt((p1.x-p2.x)*(p1.x-p2.x)+(p1.y-p2.y)*(p1.y-p2.y));
 }
 void cutp(Point &p1,Point &p2)//求圆外一点和圆的两个切点
 {
     Point E,F,G,H;
     E.x=pa.x-pr.x;
     E.y=pa.y-pr.y;
      double temp=r/dis(E,Point(,));
      F.x=E.x*temp;
     F.y=E.y*temp;
      double a=acos(temp),b=-acos(temp);
      G.x=F.x*cos(a)-F.y*sin(a);
      G.y=F.x*sin(a)+F.y*cos(a);
      H.x=F.x*cos(b)-F.y*sin(b);
      H.y=F.x*sin(b)+F.y*cos(b);
      p1.x=G.x+pr.x;
      p1.y=G.y+pr.y;
      p2.x=H.x+pr.x;
      p2.y=H.y+pr.y;
      return ;
 }
 double Larc(Point p1,Point p2)//求圆上两点的弧长
 {
     double d=dis(p1,p2);
     double a=acos((r*r+r*r-d*d)*0.5/r/r);
     return a*r;
 }
 double solve()
 {
     Point p1,p2;
     Point rl(pr.x-r,pr.y),rr(pr.x+r,pr.y);
     if(pa.x<rl.x)
         return dis(pa,rl);
     else if(pa.x>rr.x)
         return dis(pa,rr);
     else
     {
         cutp(p1,p2);
         double dis1=dis(pa,p1),dis2=dis(pa,p2);
         return min(min(Larc(rl,p1),Larc(rr,p1))+dis1,min(Larc(rl,p2),Larc(rr,p2))+dis2);
     }
 }
 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--)
     {
         scanf("%lf%lf%lf%lf%lf",&pr.x,&pr.y,&r,&pa.x,&pa.y);
         printf("%.4f\n",pi*r*0.5+solve());
     }
     return ;
 }

日常模板

　　D:一个很神奇的背包，坤神教的。首先物品中有对立的存在，所以我们把所有对立的物品分成a类和b类，这样要a[i]的话，b[i]就是另一个人的，对于每一组a,b（假设a>=b），那么两人都有b这部分，就看a-b这部分差距分给谁。那么dp[i]，就代表Miku能不能得到分到i的差距，把差距视为体积和价值，要或不要就是背包问题了。最后要差距尽可能的小，那就是从一半的差距开始分，找到第一个可以分到的差距。

 #include<cstdio>
 #include<cstdlib>
 #include<algorithm>
 using namespace std;
 const int N=;
 struct Side{
     int v,ne;
 }S[N<<];
 int sn,cnt,head[N],a[N],b[N],c[N],d[N],vis[N];
 bool dp[];
 void init(int n)
 {
     sn=cnt=;
     for(int i=;i<=n;i++)
     {
         vis[i]=;
         head[i]=-;
         a[i]=b[i]=;
     }
 }
 void add(int u,int v)
 {
     S[sn].v=v;
     S[sn].ne=head[u];
     head[u]=sn++;
 }
 void dfs(int u,int op)
 {
     vis[u]=op;
     for(int i=head[u];~i;i=S[i].ne)
         if(!vis[S[i].v])
             dfs(S[i].v,op*-);
     if(op>)
         a[cnt]+=c[u];
     else
         b[cnt]+=c[u];
 }
 int main()
 {
     int t,n,m,u,v;
     scanf("%d",&t);
     while(t--)
     {
         scanf("%d%d",&n,&m);
         init(n);
         for(int i=;i<=n;i++)
             scanf("%d",&c[i]);
         while(m--)
         {
             scanf("%d%d",&u,&v);
             add(u,v);
             add(v,u);
         }
         for(int i=;i<=n;i++)
             if(!vis[i])
             {
                 cnt++;
                 dfs(i,);
             }//先把物品分类
         int sumd=,sumi=;//sumd保持的是总的差距,差距除100离散化
         //sumi就是先保持小的总和
         for(int i=;i<=cnt;i++)
         {
             d[i]=abs(a[i]-b[i])/;
             sumd+=d[i];
             sumi+=min(a[i],b[i]);
         }
         for(int i=;i<=sumd;i++)
             dp[i]=false;
         dp[]=true;
         //01背包
         for(int i=;i<=cnt;i++)
             for(int j=sumd;j>=d[i];j--)
                 dp[j]|=dp[j-d[i]];
         for(int i=(sumd+)/;i<=sumd;i++)
             if(dp[i])
             {
                 printf("%d\n",i*+sumi);
                 break;
             }
     }
     return ;
 }

日常背包

　　J:树形dp，题目问的是异或和为0的路径包含在多少条路径之中的和，在下图中如果2到5这条路径的异或和为0，那么它就包含在3*3=9条路径中，也就是size[2]*size[5]，size是子树大小。

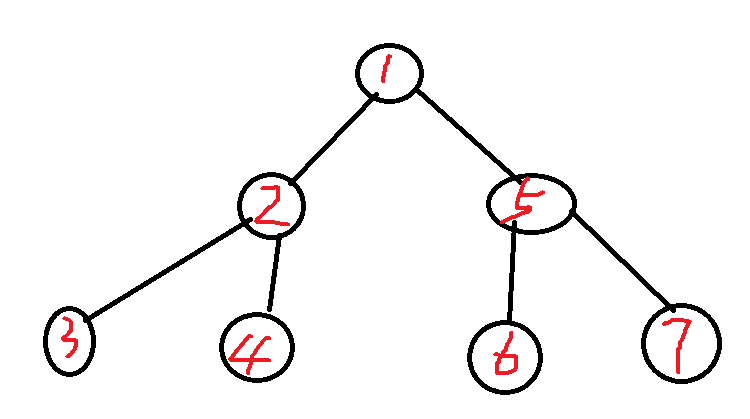
　　所以答案的统计可以分成两种，第一种是对于不在一条链上的，贡献的答案就是它们的子树大小的乘积，而第二种就是在同一条链上的就是父代节点上面的部分与子代节点子树部分的乘积。

　　我们维护一个从根节点到这个节点的异或和，假设为w,开个map，mmp[w]就记录从根节点到这个节点异或和为w的所有子树大小之和。然后，对于一个节点来说，dfs是搜索完子树之和再操作它，所以这个mmp[w]可能就包含了它子树的贡献值，这部分对第一种情况没有贡献，所以我们记录下dfs到它时的mmp，这就是不包含它子树的，然后对于第二种情况，在进入它子树的每一条链前我们就记录下mmp[w]，在搜索完这条链后，新的mmp[w]与旧的差值就是它子代节点的贡献值。

 #include<cstdio>
 #include<map>
 using namespace std;
 typedef long long ll;
 const int N=,mod=;
 struct Side{
     ll w;
     int v,ne;
 }S[N];
 int n,sn,head[N],size[N];
 ll ans;
 map<ll,ll> mmp;
 void init()
 {
     sn=ans=;
     mmp.clear();
     for(int i=;i<=n;i++)
     {
         size[i]=;
         head[i]=-;
     }
 }
 void add(int u,int v,ll w)
 {
     S[sn].w=w;
     S[sn].v=v;
     S[sn].ne=head[u];
     head[u]=sn++;
 }
 void dfs(int u,ll w)
 {
     ll num1=mmp[w],num2;
     for(int i=head[u],v;~i;i=S[i].ne)
     {
         v=S[i].v;
         num2=mmp[w];
         dfs(v,w^S[i].w);
         size[u]+=size[v];
         ans+=1ll*(n-size[v])*(mmp[w]-num2);//第二种情况与它子树的链的
         if(ans>=mod)
             ans%=mod;
     }
     ans+=1ll*num1*size[u];//第一种情况，与其他链的
     if(ans>=mod)
         ans%=mod;
     mmp[w]+=size[u];
     if(mmp[w]>=mod)
         mmp[w]%=mod;
 }
 int main()
 {
     int f;
     ll w;
     while(~scanf("%d",&n))
     {
         init();
         for(int i=;i<=n;i++)
         {
             scanf("%d%lld",&f,&w);
             add(f,i,w);
         }
         dfs(,0ll);
         printf("%lld\n",ans);
     }
     return ;
 }

日常dp

　　最后E，坤神已经补出来了，等我补了再更。