数学建模python matlab 编程(椭圆声学原理画图证明,解析几何)
证明,在椭圆形的音乐厅内,从一个椭圆的一个焦点发出声音,则另一个焦点听到的声音是最大的。
分析:证明,从椭圆的一个焦点任意发射的直线经过反射后,并经过另一个焦点。
画图,过一个焦点随机画一条直线l1,再做它与椭圆的交点,过该点作椭圆的一条切线l2,在作一条与该切线垂直的线l3,再作一条l1关于l3对称的直线l4,然后计算另一个焦点到l4的距离小于一个很小的数即可

我的matlab代码
% 画出一个椭圆
t=linspace(0,2*pi,1000);
A=5;
B=4;
C=3;
X=5*cos(t);
Y=4*sin(t);
plot(X,Y),grid on,hold on;
aa=[-3,3]
bb=[0,0]
plot(aa,bb,'o'),hold on;
axis equal % 随机画出一条直线
k=unifrnd(-10,10);
x0=-3;y0=0;
b=y0-k*x0;
x=-6:6;
y=k*x+b;
plot(x,y),hold on; % 求椭圆和直线的交点
% (m,n)为切点
syms u v
s=solve(u^2/5^2+v^2/4^2==1,v==k*u+b,u,v)
u=double(s.u)
v=double(s.v) if u(1)>u(2)
mx=1
else
mx=2
end % 过(m,n)点求切线
% mx/a? + ny/b? =1
kq=-B*B*(u(mx))/(A*A*v(mx))
bq=B*B/v(mx)
x2=-6:6;
y2=kq*x2+bq;
plot(x2,y2),hold on; % 做一条垂直于切线的线
kq2=-1/kq;
bq2=v(mx)-kq2*u(mx);
y3=kq2*x2+bq2;
plot(x2,y3,'--'),hold on; % 求出一条直线 关于y3这条直线垂直的直线
% 先找到原直线上任意一点
x0=0
y0=k*x0+b; % 找到该点关于直线的对称点
A3=kq2;B3=-1;C3=bq2;
x11 = ((B3*B3-A3*A3)*x0-2*A3*B3*y0-2*A3*C3)/(A3*A3+B3*B3)
y11 = ((A3*A3-B3*B3)*y0-2*A3*B3*x0-2*B3*C3)/(A3*A3+B3*B3)
k4=(y11-v(mx))/(x11-u(mx))
b4=v(mx)-k4*u(mx)
x4=-6:6;
y4=k4*x4+b4;
plot(x11,y11,'o'),hold on;
plot(x0,y0,'o'),hold on;
plot(x4,y4),hold on; % 点到直线y4的距离小于一个很小数
x5=-C;y5=0;
A4=k4;B4=-1;C4=b4;
d = abs(A4*x5+B4*y5+C4)/(sqrt(A4*A4-B4*B4))
d<=0.0000001
再跑个循环,多画几条
% 画出一个椭圆
t=linspace(0,2*pi,1000);
A=5;
B=4;
C=3;
X=5*cos(t);
Y=4*sin(t);
plot(X,Y),grid on,hold on;
aa=[-3,3]
bb=[0,0]
plot(aa,bb,'o'),hold on;
axis equal for tt=1:5
% 随机画出一条直线
k=unifrnd(-10,10);
x0=-3;y0=0;
b=y0-k*x0;
x=-6:6;
y=k*x+b;
plot(x,y),hold on; % 求椭圆和直线的交点
% (m,n)为切点
syms u v
s=solve(u^2/5^2+v^2/4^2==1,v==k*u+b,u,v)
u=double(s.u)
v=double(s.v) if u(1)>u(2)
mx=1
else
mx=2
end % 过(m,n)点求切线
% mx/a? + ny/b? =1
kq=-B*B*(u(mx))/(A*A*v(mx))
bq=B*B/v(mx)
x2=-6:6;
y2=kq*x2+bq;
plot(x2,y2),hold on; % 做一条垂直于切线的线
kq2=-1/kq;
bq2=v(mx)-kq2*u(mx);
y3=kq2*x2+bq2;
plot(x2,y3,'--'),hold on; % 求出一条直线 关于y3这条直线垂直的直线
% 先找到原直线上任意一点
x0=0
y0=k*x0+b; % 找到该点关于直线的对称点
A3=kq2;B3=-1;C3=bq2;
x11 = ((B3*B3-A3*A3)*x0-2*A3*B3*y0-2*A3*C3)/(A3*A3+B3*B3)
y11 = ((A3*A3-B3*B3)*y0-2*A3*B3*x0-2*B3*C3)/(A3*A3+B3*B3)
k4=(y11-v(mx))/(x11-u(mx))
b4=v(mx)-k4*u(mx)
x4=-6:6;
y4=k4*x4+b4;
plot(x11,y11,'o'),hold on;
plot(x0,y0,'o'),hold on;
plot(x4,y4),hold on;
end % 点到直线y4的距离小于一个很小数
x5=-C;y5=0;
A4=k4;B4=-1;C4=b4;
d = abs(A4*x5+B4*y5+C4)/(sqrt(A4*A4-B4*B4))
d<=0.0000001
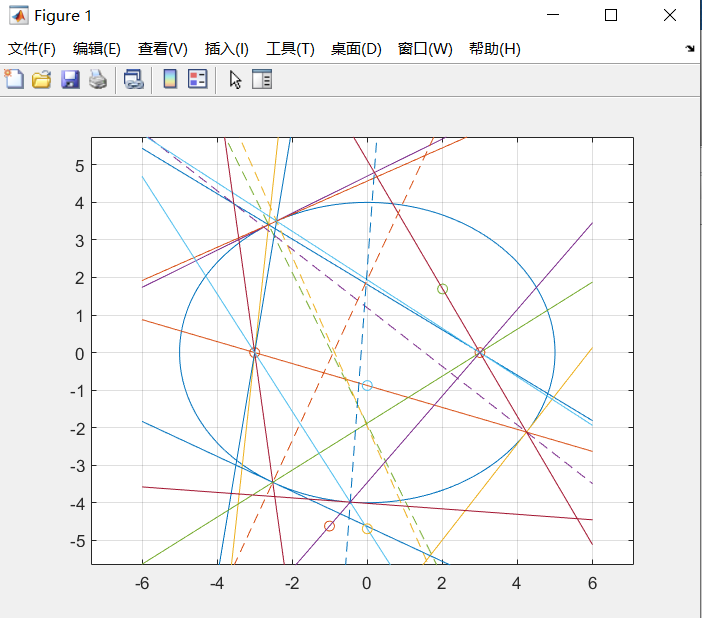
老师的matlab代码
clear;
a=3;b=2;c=sqrt(a^2-b^2);
%f = @(x) x.^2; %%%%%% 定义函数y=x^2;
f=@(x)b*(1-x.^2.*1/a.^2).^0.5; %%%%%% 定义函数(x^2)/4+(y^2)/9=1;
x=-1*a:0.1:a;
y=f(x);
x1=-1.5;y1=f(x1); %确定出切点
k1=-1*(b^2/a^2)*x1/y1;
A1=atan(k1)*180/pi;
plot(x,y); %画出椭圆的上半段
hold on; f = @(x) k1*(x-x1)+y1;
x=-1*c-1:0.1:x1+2;
y=f(x);
plot(x,y);
hold on; %画出切线 f = @(x) -1*b*(1-x.^2.*1/a.^2).^0.5; %%%%%% 定义函数(x^2)/4+(y^2)/9=1;
x = -1*a:0.1:a;
y = f(x);
plot(x,y);
hold on; %画出椭圆的下半段 plot(-1*c,0,c,0,'.'); %画出两个焦点
hold on;
line([-1*c,x1],[0,y1]);
hold on; %画出左焦点到切点间的直线 x2=-1*c;y2=0;
k2=(y1-y2)/(x1-x2);
A2=atan(k2)*180/pi;
A3=abs(A2-A1);
A4=A1-A3+180;
B4=A4*pi/180;
k4=tan(B4); f = @(x) k4*(x-x1)+y1;
x=x1:0.1:c;
y=f(x);
plot(x,y);
hold on; %画出反射线 axis([-4 4 -3 3])
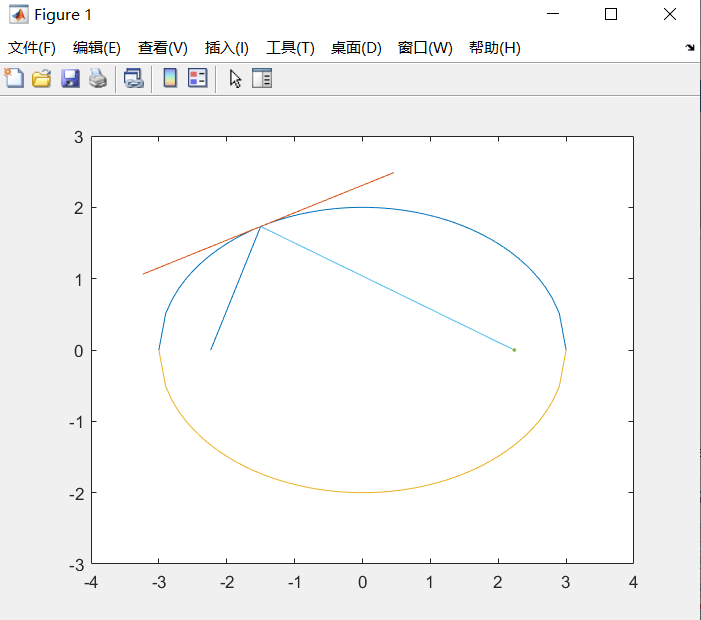
数学建模python matlab 编程(椭圆声学原理画图证明,解析几何)的更多相关文章
- 数学建模python matlab 编程(疾病传播模型)
例12:一只游船上有800(1000)人,一名游客不慎患传染病,12(10)小时后有3人发病,由于船上不能及时隔离,问经过60(30)小时,72小时,患此病的人数.(与人口模型和Logistic模型类 ...
- 数学建模python matlab 编程(指派问题)
指派授课问题 现有A.B.C.D四门课程,需由甲.乙.丙.丁四人讲授,并且规定: 每人只讲且必须讲1门课:每门课必须且只需1人讲. 四人分别讲每门课的费用示于表中: 课 费用 人 A B C D 甲 ...
- 数学建模python matlab 编程(随机游走问题)
1 (1). 随机游走问题.在-10到10的一维线段上,质点以1/5的概率用左运动1单位,以2/5的概率停止不动,以2/5的概率向右运动2单位,且碰到-10时向右运动3单位,碰到10时向左运动4单位. ...
- 数学建模python matlab 编程(喷泉模拟)
在无风情况下的喷泉模拟 我的python代码 import numpy as np import random import matplotlib matplotlib.rcParams['font. ...
- 在数学建模中学MATLAB
为期三周的数学建模国赛培训昨天正式结束了,还是有一定的收获的,尤其是在MATLAB的使用上. 1. 一些MATLAB的基础性东西: 元胞数组的使用:http://blog.csdn.net/z1137 ...
- 【数学建模】MatLab 数据读写方法汇总
1.读入 txt 文件数据. load xxx.txt A=load(‘xxx.txt’) A=dlmread(‘xxx.txt’) A=importdata(‘xxx.txt’) 例:将身高体重的 ...
- 【数学建模】MATLAB语法
一.向量.矩阵的表示和使用 format long %小数很多format short %默认4位小数format rat %显示最近的分数format short e %指数格式的数 尾数多少 e ...
- 【数学建模】MATLAB学习笔记——函数式文件
MATLAB学习笔记——函数式文件 引入函数式文件 说明: 函数式文件主要用于解决计算中的参数传递和函数调用的问题. 函数式的标志是它的第一行为function语句. 函数式文件可以有返回值,也可以没 ...
- Matlab 多个版本的安装包下载、安装和激活教程 + 多套数学建模视频教程
目录 1. 关键词 1.1. 说明 2. 下载地址 2.1. OneDrive高速云盘 2.1.1. 多版本的安装包 2.1.2. 多套数学建模的视频教程 2.2. 百度云 3. 安装教程 1. 关键 ...
随机推荐
- Kinect视频中运用全身运动和人体测量统计学的人物识别技术
摘要: 对于人物识别技术来说,动作和人体测量统计学对于光学差异并不敏感,甚至对于眼镜,头发,帽子的描述相当粗糙,现在的以步态为基础的识别技术都是基于对细节的精确描述和对步态周期的精确测量.这种方法需要 ...
- Python Scrapy爬虫框架之初次使用
此篇博客为本人对小甲鱼的课程的总结. 关于Scrapy的安装网上都有方法,这里便不再叙述. 使用Scrapy抓取一个网站一共需要四个步骤: 0.创建一个Scrapy项目: 1.定义Item容器: 2. ...
- 构建官方example
开发工具的选择: 构建官方example:
- 关于bash这类脚本语言的一点感想
写了几百行bash玩具代码, 越发觉得,动态语言不适合做大型项目,写起来倒是爽,但是没有类型检查,变量名拼错了还不知道 再加上各种奇葩变量满天飞,啧啧
- 不同显卡对mrt 的支持
ios bits限制大概512bits 低端256bits mali 也是bits限制 2017年 Mali-T760 128bits adreno android显卡4 肯定可以 因为deferre ...
- css居然有根据容器宽度自动截取长度加省略号功能,强大!!
作者:☆威廉古堡♂ 项目中最初的做法(js截取): //字符长度截取包括中英文混合 function subStr(str, len) { str = str.toString(); var newL ...
- [MySQL优化] -- 如何定位效率较低的SQL
一般通过以下两种方式定位执行效率较低的 SQL 语句. 通过慢查询日志定位那些执行效率较低的 SQL 语句,用 --log-slow-queries[=file_name] 选项启动时, mysqld ...
- 在laravel5.8中集成swoole组件----用协程实现的服务端和客户端(nginx配置篇章)
laravel项目中的配置 原文出处:https://laravelacademy.org/post/19700.html,感谢原文作者让laravel这款可爱的php框架,进入了高并发的殿堂 如果 ...
- Educational Codeforces Round 73 (Rated for Div. 2) D. Make The Fence Great Again(DP)
链接: https://codeforces.com/contest/1221/problem/D 题意: You have a fence consisting of n vertical boar ...
- eq(index|-index)
eq(index|-index) 概述 获取当前链式操作中第N个jQuery对象,返回jQuery对象,当参数大于等于0时为正向选取,比如0代表第一个,1代表第二个.当参数为负数时为反向选取,比如-1 ...
