[CSP-S模拟测试]:B（期望DP）

题目传送门（内部题151）

---

输入格式

　　第一行一个整数$N$。
　　第二行$N$个整数，第$i$个为$a_i$。

---

输出格式

　　一行一个整数，表示答案。为避免精度误差，答案对$323232323$取模。
　　即设答案化为最简分式后的形式为$\frac{a}{b}$，其中$a$和$b$互质。输出整数$x$使得$bx\equiv a(\mod 323232323)$且$0\leqslant x<323232323$。可以证明这样的整数$x$是唯一的。

---

样例

样例输入：

3
2 3 3

样例输出：

202020207

---

数据范围与提示

　　每个测试点$10$分，共$10$个测试点：

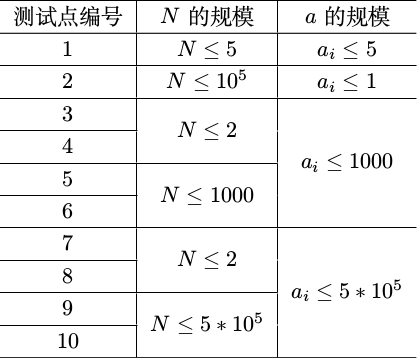
　　对于所有的数据，有：$1\leqslant N,a_i$。

---

题解

考虑$DP$，设$f_i$表示$a_i$被选的期望次数，注意这里是$a_i$。

那么答案就是：

$$ans=\sum\limits_{i=2}^nf_{a_i}}+a_1$$

想办法求出$f_i$。

考虑从$N\leqslant 2$入手，相当于是从$(a_1,a_i)$走到坐标轴的期望次数，每次都有$\frac{1}{2}$的概率走不同的方向；类比这种做法，可以列出$a_i$的贡献式子：

$$\sum\limits_{i=0}^{a_i-1}i\times \frac{C_{a_1-1+i}^i}{2^{a_1+i}}+a_i\times (1-\sum\limits_{i=0}^{a_i-1}\frac{C_{a_1-1+i}^i}{2^{a_1+i}}$$

看似还是$\Theta(N^2)$的，但是实际上我们可以线性递推出来$f[i]$，然后直接统计答案就好了。

时间复杂度：$\Theta(\max(a_i))$。

期望得分：$100$分。

实际得分：$100$分。

---

代码时刻

#include<bits/stdc++.h>
using namespace std;
const int mod=323232323;
const int in2=161616162;
int N;
int a[500001];
long long fac[500001],inv[500001];
long long f[500001],w,p,inc,res;
long long ans;
long long qpow(long long x,long long y)
{
	long long res=1;
	while(y)
	{
		if(y&1)res=res*x%mod;
		x=x*x%mod;y>>=1;
	}
	return res;
}
void pre_work()
{
	fac[0]=1;
	for(int i=1;i<=500000;i++)fac[i]=fac[i-1]*i%mod;
	inv[500000]=qpow(fac[500000],mod-2);
	for(int i=500000;i;i--)inv[i-1]=inv[i]*i%mod;
}
long long C(int x,int y){return fac[x]*inv[y]%mod*inv[x-y]%mod;}
int main()
{
	pre_work();
	scanf("%d",&N);
	for(int i=1;i<=N;i++)
		scanf("%d",&a[i]);
	inc=p=qpow(qpow(2,a[1]),mod-2);
	for(int i=1;i<=500000;i++)
	{
		inc=inc*in2%mod;
		f[i]=(w+i*(1-p)+mod)%mod;
		res=C(a[1]-1+i,i)*inc%mod;
		p=(p+res)%mod;w=(w+res*i)%mod;
	}
	ans=a[1];
	for(int i=2;i<=N;i++)ans=(ans+f[a[i]]+mod)%mod;
	printf("%lld",ans);
	return 0;
}

---

rp++