Codeforces 15 E. Triangles

http://codeforces.com/problemset/problem/15/E

题意：

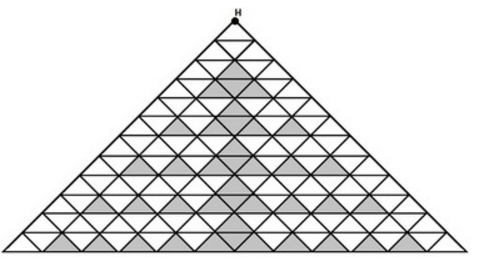
从H点走下去，再走回H点，不能走重复路径，且路径不能把黑色三角形包围的方案数

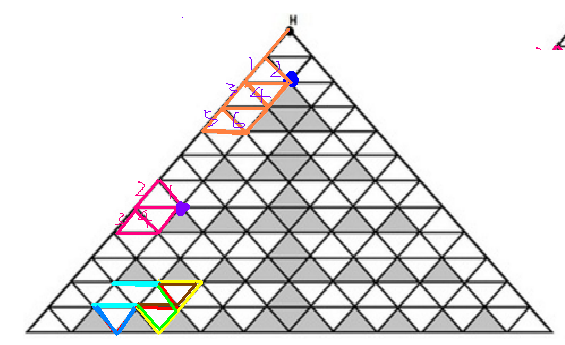
中间的黑色三角形把整张图分成两部分

即如果想要走回H点，除了只第一行的路径，必经过上面的蓝色点

否则一定会包围黑色的三角形

设从H往左下走，又回到蓝色点的方案数为S

那么 ans=（S*S+1）* 2

S*S 是因为左右两边是等价的

加1是不经过蓝色点的那一条路径

再乘2是先向左和先向右是两种方案

如何求S？

将两行看做一层

设f[i] 表示最远到第i层，回到蓝点的方案数，那么S= 6 + Σ f[i]，i∈[3,n/2]

6是前两层的方案数，因为前两层不需要考虑向内凹进的部分，所以单独计算

从第三层开始，要考虑向内凹的白色三角形

假设现在是算f[x]

那么 从H到第x层的方案数只有一种，就是沿着最左边一路往下

凹进的白色三角形每三个斜着的看做一组

设g[i] 表示凹进的白色三角形有i组，走进去在出来的方案数

必经上图中的紫色点

想要到第i组，那么前i-1组在进去的时候，可以水平向右，也可以向右下

到第i组要拐弯的时候，可以先水平向右或右下，再向左上或右上

拐完弯出去的时候，只能一直水平向左走

所以g[i]=g[i-1]+2^(i+1)

第x层的白色三角形有x-2组

推式子可以得到 g[x]=2^x - 4

再加上不走进去的一种方案，对于第x层的凹进去的白色三角形一共有2^x-4+1中方案

在第x层拐弯的时候，有4中方案，如上图中的粉色路径

所以f[x] = 4* π （2^k-3） k∈[3,x]

所以答案为

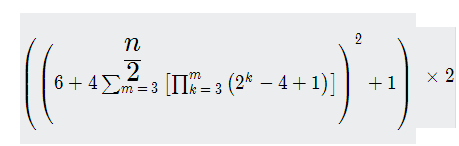
#include<cstdio>
 
using namespace std;
 
const int mod=;
 
int main()
{
    int n;
    scanf("%d",&n);
    if(n==)
    {
        printf("");
        return ;
    }
    long long xigema=,pai=,pow=;
    int m=n/;
    for(int i=;i<=m;++i)
    {
        (pow*=)%=mod;
        (pai*=pow-+)%=mod;
        (xigema+=pai)%=mod;
    }
    xigema*=;
    xigema+=;
    xigema%=mod;
    (xigema*=xigema)%=mod;
    xigema++;
    (xigema*=)%=mod;
    printf("%I64d",xigema);
}