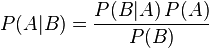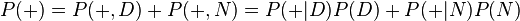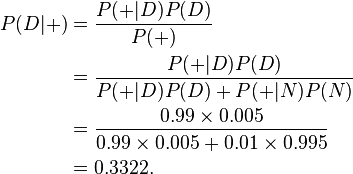Python 贝叶斯分类
很久的时间没有更新了,一是因为每天加班到比较晚的时间,另外,公司不能上网,回家后就又懒得整理,最近在看机器学习实战的书籍,因此才又决定重新拾起原先的博客!
今天讲的是第三章的贝叶斯分类方法,我们从一个简简单单的例子开始入手:首先看(1)图中的例子,假设有一个装了7块时候的罐子,其中3块时黑色的,4块时白色的,从中随机取出一个石头,那么这个石头是灰色的概率是多大?


(1) (2)
我们可以很轻易的计算出取出一个灰色球的概率是4/7,取出一个黑色球的概率是3/7,但是假如这些球被放在两个不同的罐子中,如图(2) :A中有3个黑球,2个灰球,B中有三个灰球,两个黑球。那我们从中取出一个灰球的概率是多大?我们很自然的联想到要首先知道是从A中去取还是从B中去取。
假设从A中取得概率为Pa,从B中取得概率为Pb,那么我们取出一个灰色球的概率为:
Pgray = ( 0.4 ) * Pa + ( 0.6 )* Pb
此时的0.4 和0.6 分别表示为从A和B桶中取出一个灰色球的概率,我们也称其为条件概率, 记为P(gray | A) = 0.4,P(gray|B) = 0.6
我们引出维基百科上关于贝叶斯公式的定义:
贝叶斯定理是关于随机事件A和B的条件概率(或边缘概率)的一则定理。
其中P(A|B)是在B发生的情况下A发生的可能性。贝叶斯定理中,每个名词都有约定俗成的名称:
按这些术语,Bayes定理可表述为:
后验概率 = (相似度*先验概率)/标准化常量
也就是说,后验概率与先验概率和相似度的乘积成正比。
另外,比例P(B|A)/P(B)也有时被称作标准相似度(standardised likelihood),Bayes定理可表述为:
后验概率 = 标准相似度*先验概率
[例一(维基百科)]
贝叶斯定理在检测吸毒者时很有用。假设一个常规的检测结果的敏感度与可靠度均为99%,也就是说,当被检者吸毒时,每次检测呈阳性(+)的概率为99%。而被检者不吸毒时,每次检测呈阴性(-)的概率为99%。从检测结果的概率来看,检测结果是比较准确的,但是贝叶斯定理却可以揭示一个潜在的问题。假设某公司将对其全体雇员进行一次鸦片吸食情况的检测,已知0.5%的雇员吸毒。我们想知道,每位医学检测呈阳性的雇员吸毒的概率有多高?令“D”为雇员吸毒事件,“N”为雇员不吸毒事件,“+”为检测呈阳性事件。可得
- P(D)代表雇员吸毒的概率,不考虑其他情况,该值为0.005。因为公司的预先统计表明该公司的雇员中有0.5%的人吸食毒品,所以这个值就是D的先验概率。
- P(N)代表雇员不吸毒的概率,显然,该值为0.995,也就是1-P(D)。
- P(+|D)代表吸毒者阳性检出率,这是一个条件概率,由于阳性检测准确性是99%,因此该值为0.99。
- P(+|N)代表不吸毒者阳性检出率,也就是出错检测的概率,该值为0.01,因为对于不吸毒者,其检测为阴性的概率为99%,因此,其被误检测成阳性的概率为1-99%。
- P(+)代表不考虑其他因素的影响的阳性检出率。该值为0.0149或者1.49%。我们可以通过全概率公式计算得到:此概率 = 吸毒者阳性检出率(0.5% x 99% = 0.495%)+ 不吸毒者阳性检出率(99.5% x 1% = 0.995%)。P(+)=0.0149是检测呈阳性的先验概率。用数学公式描述为:
根据上述描述,我们可以计算某人检测呈阳性时确实吸毒的条件概率P(D|+):
尽管我们的检测结果可靠性很高,但是只能得出如下结论:如果某人检测呈阳性,那么此人是吸毒的概率只有大约33%,也就是说此人不吸毒的可能性比较大。我们测试的条件(本例中指D,雇员吸毒)越难发生,发生误判的可能性越大。(这个相信能给曾经去体检结果非常不好的人一个乐观的消息)
[例二 (Machine Learn in Action)]
机器学习的一个非常重要的作用就是对文本进行分类,我们使用Python进行文本的分类
(未完待续)
参考:[1]刘未鹏 数学之美番外篇:平凡而又神奇的贝叶斯方法
[2] Machine Learn in Action, Peter Harrington
Python 贝叶斯分类的更多相关文章
- 朴素贝叶斯分类器及Python实现
贝叶斯定理 贝叶斯定理是通过对观测值概率分布的主观判断(即先验概率)进行修正的定理,在概率论中具有重要地位. 先验概率分布(边缘概率)是指基于主观判断而非样本分布的概率分布,后验概率(条件概率)是根据 ...
- 朴素贝叶斯分类算法介绍及python代码实现案例
朴素贝叶斯分类算法 1.朴素贝叶斯分类算法原理 1.1.概述 贝叶斯分类算法是一大类分类算法的总称 贝叶斯分类算法以样本可能属于某类的概率来作为分类依据 朴素贝叶斯分类算法是贝叶斯分类算法中最简单的一 ...
- (数据科学学习手札30)朴素贝叶斯分类器的原理详解&Python与R实现
一.简介 要介绍朴素贝叶斯(naive bayes)分类器,就不得不先介绍贝叶斯决策论的相关理论: 贝叶斯决策论(bayesian decision theory)是概率框架下实施决策的基本方法.对分 ...
- R&python机器学习之朴素贝叶斯分类
朴素贝叶斯算法描述应用贝叶斯定理进行分类的一个简单应用.这里之所以称之为“朴素”,是因为它假设各个特征属性是无关的,而现实情况往往不是如此. 贝叶斯定理也称贝叶斯推理,早在18世纪,英国学者贝叶斯(1 ...
- 《机器学习实战》基于朴素贝叶斯分类算法构建文本分类器的Python实现
============================================================================================ <机器学 ...
- 利用朴素贝叶斯分类算法对搜狐新闻进行分类(python)
数据来源 https://www.sogou.com/labs/resource/cs.php介绍:来自搜狐新闻2012年6月—7月期间国内,国际,体育,社会,娱乐等18个频道的新闻数据,提供URL ...
- 机器学习之路: python 朴素贝叶斯分类器 MultinomialNB 预测新闻类别
使用python3 学习朴素贝叶斯分类api 设计到字符串提取特征向量 欢迎来到我的git下载源代码: https://github.com/linyi0604/MachineLearning fro ...
- python实现一个朴素贝叶斯分类方法
1.公式 上式中左边D是需要预测的测试数据属性,h是需要预测的类:右边式子分子是属性的条件概率和类别的先验概率,可以从统计训练数据中得到,分母对于所有实例都一样,可以不考虑,所有只需 ,返回最大概率的 ...
- Python数据科学手册-机器学习:朴素贝叶斯分类
朴素贝叶斯模型 朴素贝叶斯模型是一组非常简单快速的分类方法,通常适用于维度非常高的数据集.因为运行速度快,可调参数少.是一个快速粗糙的分类基本方案. naive Bayes classifiers 贝 ...
随机推荐
- Centos7安装OpenLDAP
https://www.cnblogs.com/zhaijunming5/p/9522756.html
- 对MariaDB10.0的Sphinx进行扩展
已修改过的文件:http://pan.baidu.com/s/1o8DHvkA 将这两个文件放到MariaDB的解压目录后,再进行安装 /usr/local/mariadb-10.0.28/stora ...
- Delphi---TServerSocket和TClientSocket发送和接收大数据包
https://www.cnblogs.com/zhangzhifeng/p/6065244.html TServerSocket和TClientSocket用非阻塞模式发送和接收比较大的数据时,可能 ...
- POJ 3126 Prime Path (素数+BFS)
题意:给两个四位素数a和b,求从a变换到b的最少次数,每次变换只能变换一个数字并且变换的过程必须也是素数. 思路:先打表求出四位长度的所有素数,然后利用BFS求解.从a状态入队,然后从个位往千位的顺序 ...
- #1 // BZOJ 4361 isn
Description 给出一个长度为n的序列A(A1,A2...AN).如果序列A不是非降的,你必须从中删去一个数, 这一操作,直到A非降为止.求有多少种不同的操作方案,答案模10^9+7. 题 ...
- 065 xftp的使用
1.xftp 一个基于 MS windows 平台的功能强大的SFTP.FTP 文件传输软件 2.下载安装 *3.在linux上安装服务 sudo yum install vsftp
- Flutter常用组件(Widget)解析-Scaffold
实现一个应用基本的布局结构. 举个栗子: import 'package:flutter/material.dart'; void main() => runApp(MyApp()); clas ...
- EF连接字符串小问题记录
1.EFDbContext”不包含必需的 providerName 特性: <connectionStrings> <add name="EFDbContext" ...
- idea模板注释
类文件头部的注释 #if (${PACKAGE_NAME} && ${PACKAGE_NAME} != "")package ${PACKAGE_NAME};#en ...
- 智能优化 之 下山单纯形法 C++
单纯形法简介在其他网站上都可以查到,我就不多说了 我们主要说方法 它主要解决的是局部最优解的问题 利用多边形进行求解的,若有n个变量,则利用n+1边形 我们这里以两个变量为例,求解第三维度的最优解 例 ...