内部排序->交换排序->快速排序
文字描述
快速排序是对起泡排序的一种改进。它的基本思想是,通过一趟排序将待排序记录分割成独立的两部分,其中一部分记录的关键字均比另一部分记录的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。
一趟快速排序描述:假设待排序的序列为{L.r[s], L.r[s+1], … , L.r[t]},首先任意选取一个记录(通常选第一个记录L.r[s])作为枢轴(pivot), 然后按下述原则重新排列其余记录:将所有关键字较它小的记录都安置在它的位置之前,将所有关键字较它大的记录都安置在它的位置之后。由此以该“枢轴”记录最后所落得位置i作分界线,将序列{L.r[s], L.r[s+1], … , L.r[t]}分割成两个子序列{L.r[s], L.r[s+1], …, L.r[i-1]}和{L.r[i+1], L.r[i+2], …, L.r[t]}。至此,完成一趟快速排序。
示意图

算法分析
快速排序的平均时间为knlnn, 其中n为记录个数,k为某个常数。经验证明,在所有同数量级(nlogn)的排序方法中,其平均时间性能最好。但是,若初始记录序列按关键字有序或基本有序时,快速排序将蜕化为起泡排序,其时间复杂度为n*n.
辅助空间为1,但是需要一个栈空间来实现递归。若每趟排序都将记录序列均匀的分割成长度相接近的两个子序列,则栈的最大深度为[log2n]+1;若每趟排序之后,枢轴位置都在最边上,则栈的最大深度为n。
是不稳定的排序方法
代码实现
#include <stdio.h>
#include <stdlib.h> #define DEBUG #define EQ(a, b) ((a) == (b))
#define LT(a, b) ((a) < (b))
#define LQ(a, b) ((a) <= (b)) #define MAXSIZE 20
typedef int KeyType;
typedef char InfoType;
typedef struct{
KeyType key;
InfoType otherinfo;
}RedType; typedef struct{
RedType r[MAXSIZE+];
int length;
}SqList; void PrintList(SqList L){
int i = ;
printf("下标值:");
for(i=; i<=L.length; i++){
printf("[%d] ", i);
}
printf("\n关键字:");
for(i=; i<=L.length; i++){
printf(" %-3d", L.r[i].key);
}
printf("\n其他值:");
for(i=; i<=L.length; i++){
printf(" %-3c", L.r[i].otherinfo);
}
printf("\n\n");
return ;
} /*
*交换顺序表L中子表L.r[low,...,high]的纪录,枢轴记录到位,
*并返回其所在位置,此时在它之前(后)均不大于(小于)它
*/
int Partition(SqList *L, int low, int high)
{
//用字表的第一个记录作枢轴纪录
L->r[] = L->r[low];
//pivotkey表示枢轴记录的关键字值
KeyType pivotkey = L->r[low].key; //从表的两端交替向中间扫描
while(low<high){
//将比枢轴记录小的记录移到低端
while(low<high && L->r[high].key>=pivotkey) --high;
L->r[low] = L->r[high]; //将比枢轴记录大的记录移到高端
while(low<high && L->r[low].key<=pivotkey) ++low;
L->r[high] = L->r[low];
}
//枢轴记录到位
L->r[low] = L->r[];
//返回枢轴位置
return low;
} /*
* 对顺序表L中子表L.r[low,...,high]作快速排序
*/
void QSort(SqList *L, int low, int high)
{ KeyType pivotkey;
if(low<high){
//将L.r[low,...,high]一分为二,低(高)于pivotkey的均不大于(小于)它
pivotkey = Partition(L, low, high);
#ifdef DEBUG
printf("一趟快速排序后(low=%d, high=%d), pivotkey=%d\n",low, high, pivotkey);
PrintList(*L);
#endif
//对低字表递归排序,pivotkey是轴枢位置
QSort(L, low, pivotkey-);
//对高子表递归排序
QSort(L, pivotkey+, high);
}
} /*对顺序表L作快速排序*/
void QuickSort(SqList *L)
{
printf("对顺序表L作快速排序:\n\n");
QSort(L, , L->length);
} int main(int argc, char *argv[])
{
if(argc < ){
return -;
}
SqList L;
int i = ;
for(i=; i<argc; i++){
if(i>MAXSIZE)
break;
L.r[i].key = atoi(argv[i]);
L.r[i].otherinfo = 'a'+i-;
}
L.length = (i-);
L.r[].key = ;
L.r[].otherinfo = '';
printf("输入数据:\n");
PrintList(L);
//对顺序表L进行快速排序
QuickSort(&L); return ;
}
快速排序
运行
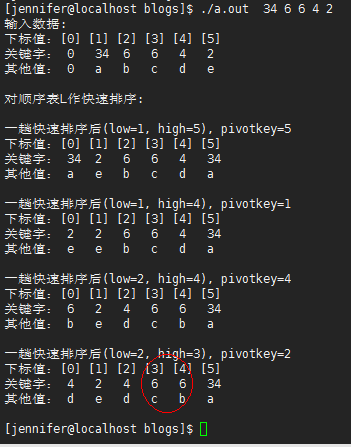
内部排序->交换排序->快速排序的更多相关文章
- 内部排序->交换排序->起泡排序
文字描述 首先将第一个记录的关键字和第二个记录的关键字进行比较,若为逆序(L.r[1].key>L.r[2].key),则将两个记录交换位置,然后比较第二个记录和第三个记录的关键字.依次类推,直 ...
- 排序算法练习--JAVA(:内部排序:插入、选择、冒泡、快速排序)
排序算法是数据结构中的经典算法知识点,也是笔试面试中经常考察的问题,平常学的不扎实笔试时候容易出洋相,回来恶补,尤其是碰到递归很可能被问到怎么用非递归实现... 内部排序: 插入排序:直接插入排序 选 ...
- 内部排序比较(Java版)
内部排序比较(Java版) 2017-06-21 目录 1 三种基本排序算法1.1 插入排序1.2 交换排序(冒泡)1.3 选择排序(简单)2 比较3 补充3.1 快速排序3.2 什么是桶排序3.3 ...
- Java实现各种内部排序算法
数据结构中常见的内部排序算法: 插入排序:直接插入排序.折半插入排序.希尔排序 交换排序:冒泡排序.快速排序 选择排序:简单选择排序.堆排序 归并排序.基数排序.计数排序 直接插入排序: 思想:每次将 ...
- 用 Java 实现常见的 8 种内部排序算法
一.插入类排序 插入类排序就是在一个有序的序列中,插入一个新的关键字.从而达到新的有序序列.插入排序一般有直接插入排序.折半插入排序和希尔排序. 1. 插入排序 1.1 直接插入排序 /** * 直接 ...
- 七种机器内部排序的原理与C语言实现,并计算它们的比较次数与移动次数。
内部排序是指待排序列完全存放在内存中所进行的排序过程,适合不太大的元素序列. 排序是计算机程序设计中的一种重要操作,其功能是对一个数据元素集合或序列重新排列成一个按数据元素某个相知有序的序列.排序分为 ...
- 内部排序->其它->地址排序(地址重排算法)
文字描述 当每个记录所占空间较多,即每个记录存放的除关键字外的附加信息太大时,移动记录的时间耗费太大.此时,就可以像表插入排序.链式基数排序,以修改指针代替移动记录.但是有的排序方法,如快速排序和堆排 ...
- 内部排序->归并排序->2-路归并排序
文字描述 假设初始序列有n个记录,则可看成是n个有序的字序列,每个字序列的长度为1,然后两两归并,得到[n/2]个长度为2或1的有序子序列:再两两归并,…, 如此重复,直到得到一个长度为n的有序序列为 ...
- 交换排序—快速排序(Quick Sort)原理以及Java实现
交换排序—快速排序(Quick Sort) 基本思想: 1)选择一个基准元素,通常选择第一个元素或者最后一个元素, 2)通过一趟排序讲待排序的记录分割成独立的两部分,其中一部分记录的元素值均比基准元素 ...
随机推荐
- MXNET:权重衰减-gluon实现
构建数据集 # -*- coding: utf-8 -*- from mxnet import init from mxnet import ndarray as nd from mxnet.gluo ...
- [转]JSTL 自定义方法报错Invalid syntax for function signature in TLD.
Apache Tomcat/6.0.18 ${my:splitApply(apply)} <function> <name>splitApply</name> &l ...
- C++ 智能指针四
/* 智能指针enable_shared_from_this模板类使用 */ #include <iostream> #include <string> #include &l ...
- PLSQL存储过程(基础篇)-转
我不是专门的开发人员,但存储过程又是很重要的知识,为了能够很好的记忆,现把这些基础知识总结一下.存储过程可以实现代码的充分共享,提高系统性能. 基础篇 知识回顾 如果经常使用特定操作,哪么 ...
- Asp.net常用的三十多个代码(非常实用)
1.//弹出对话框.点击转向指定页面 Response.Write("<script>window.alert('该会员没有提交申请,请重新提交!')</script> ...
- maven 打包报错(增加调试信息)
eclipse配置debug详细信息 如下图:
- mybatis xml 文件中like模糊查询
1.直接传参法 直接传参法,就是将要查询的关键字keyword,在代码中拼接好要查询的格式,如%keyword%,然后直接作为参数传入mapper.xml的映射文件中. 2.CONCAT()函数 My ...
- Windowsclient SSH 远程连接Windowsserver(PowerShell Server)
近期刚搞完SSH框架.又来研究研究SSH远程连接.为什么这么要弄这个呢?由于如今我如今开发主要在自己的笔记本(windows)上,然后写的后端都要部署到实验室的台式机(windows)上,这样一来,我 ...
- Hibernate -- Dao层 -- CURD -- 随记
根据Where 参数 查询记录总数 .拼接SQL语句 .获取Session(hibernateTemplate.getSessionFactory().getCurrentSession()),调用C ...
- 修改Ubuntu的aptget源为阿里源的方法
1.复制原文件备份sudo cp /etc/apt/sources.list /etc/apt/sources.list.bak 2.编辑源列表文件 sudo vim /etc/apt/sources ...
