Ex 6_21 最小点覆盖问题_第八次作业

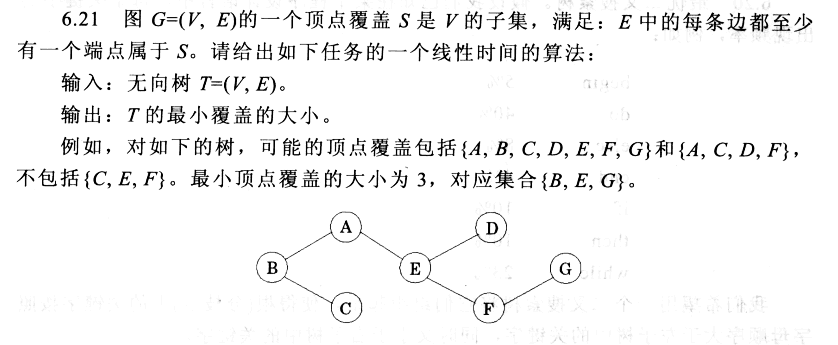
子问题定义: 对于图中的每个结点，有两种状态，即属于最小点覆盖和不属于最小点覆盖，定义minSet[i][0]表示结点i属于点覆盖，并且以i为根的树的最小点覆盖的大小。minSet[i][1]表示点i不属于点覆盖，并且以i为根的树的最小点覆盖的大小。

递归关系:

对于minSet[i][0],i的孩子结点可以属于点覆盖，也可以不属于点覆盖，取其使以i为根的子树的点覆盖最小的情况，因此

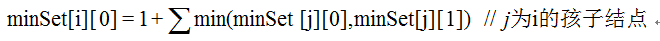
　　对于minSet[i][1],由于i不属于点覆盖，因此其所有孩子结点都必须属于点覆盖，因此

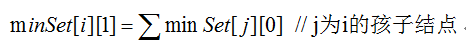
初值设定：

minSet[i][0]=1

minSet[i][1]=0

求解顺序：

从树的叶子结点开始求每个结点的最小点覆盖，自底向上，最后比较minSet[root][0]与minSet[root][1]的大小，最小者即为最终的结果。

 package org.xiu68.ch6.ex8;
 
 import java.util.ArrayList;
 
 public class Exp6_21 {
 
     public static void main(String[] args) {
         // TODO Auto-generated method stub
         //运行结果
         /*
          树的最大独立集为: 4
         顶点值为: 4 6 2 3
         树的最小点覆盖为: 2
         顶点值为: 5 1
         */
         //由结果可知 最大独立集与最小点覆盖集合互为补集
         ArrayList<Integer> vexs=new ArrayList<>();
         for(int i=1;i<=6;i++)
             vexs.add(i);
         //构造一个无向无环图
         int[][] edges=new int[][]{
             {0,1,1,0,0,0},
             {1,0,0,0,1,0},
             {1,0,0,0,0,0},
             {0,0,0,0,1,0},
             {0,1,0,1,0,1},
             {0,0,0,0,1,0}
         };
         MGraph<Integer> m=new MGraph<Integer>(6, 6, edges, vexs);
         m.maxIndependentSet();
         System.out.println();
         m.minCoverSet();
     }
 }
 
 //邻接矩阵表示图、无向无环图
 class MGraph<T>{
     public int vexNum;                //顶点数量
     public int edgeNum;                //边数量
     public int[][] edges;            //邻接矩阵
     public ArrayList<T> vexs;        //顶点表
 
     public int[][] maxDep;                //最大独立集
     public ArrayList<Integer> set;        //最大独立集顶点序号
 
     public int[][] minCover;            //最小点覆盖
     public ArrayList<Integer> minSet;    //最小点覆盖顶点序号
 
     public MGraph(int vexNum, int edgeNum, int[][] edges, ArrayList<T> vexs) {
         this.vexNum = vexNum;
         this.edgeNum = edgeNum;
         this.edges = edges;
         this.vexs = vexs;
 
         maxDep=new int[vexNum][2];
         set=new ArrayList<>();
 
         minCover=new int[vexNum][2];
         minSet=new ArrayList<>();
     }
 
     //最大独立集
     public void maxIndependentSet(){
         independentSet(0, 0);
 
         if(maxDep[0][0]>maxDep[0][1])
             System.out.println("树的最大独立集为: "+maxDep[0][0]);
         else
             System.out.println("树的最大独立集为: "+maxDep[0][1]);
 
         System.out.print("顶点值为: ");
         for(int i=0;i<set.size();i++)
             System.out.print(vexs.get(set.get(i))+" ");
     }
     //求以child为根的树的最大独立集
     //child:当前正在处理的结点
     //parent:child的父结点
     private void independentSet(int child,int parent){
         maxDep[child][0]=1;        //当前结点放入独立集
         maxDep[child][1]=0;        //当前结点不放入独立集
 
         for(int i=0;i<vexNum;i++){
             if(edges[child][i]==0 || i==parent)    //如果顶点间不存在边或尾结点为父结点
                 continue;
             independentSet(i, child);    
 
             //因为child加入了最大独立集，所以子结点不加入最大独立集
             //以child为根的树的最大独立集的规模为    ( 1+  child的孙子结点的最大独立集的规模  )
             maxDep[child][0]+=maxDep[i][1];       
 
             if(maxDep[i][0]>maxDep[i][1])
                 maxDep[child][1]+=maxDep[i][0];        //加入子结点
             else
                 maxDep[child][1]+=maxDep[i][1];        //不加入子结点
         }
 
         if(maxDep[child][0]>maxDep[child][1])    //比较加入child与不加入child的独立集大小，取较大者为结果
             set.add(child);
     }
 
     //***********************************************************
 
     //最小点覆盖
     public void minCoverSet(){
         coverSet(0,0);
         if(minCover[0][0]<minCover[0][1])
             System.out.println("树的最小点覆盖为: "+minCover[0][0]);
         else
             System.out.println("树的最小点覆盖为: "+minCover[0][1]);
 
         System.out.print("顶点值为: ");
         for(int i=0;i<minSet.size();i++){
             System.out.print(vexs.get(minSet.get(i))+" ");
         }
     }
     //求以child为根的树的最小点覆盖集合
     //child:当前正在处理的结点
     //parent:child的父结点
     private void coverSet(int child,int parent){
         minCover[child][0]=1;        //child放入最小点覆盖集合
         minCover[child][1]=0;        //child不放入最小点覆盖集合
 
         for(int i=0;i<vexNum;i++){
             if(edges[child][i]==0 || i==parent)    //如果顶点间不存在边或尾结点为父结点
                 continue;
 
             coverSet(i,child);
 
             //如果子结点i放入集合结果更小则把i放入集合
             if(minCover[i][0]<minCover[i][1])
                 minCover[child][0]+=minCover[i][0];        //子结点i放入集合
             else
                 minCover[child][0]+=minCover[i][1];        //子结点i不放入集合
 
             //若child不放入最小点覆盖集合，则其所有子结点都要放入最小点覆盖集合
             minCover[child][1]+=minCover[i][0];        
 
             if(minCover[child][0]<minCover[child][1])    //取最小值作为结果
                 minSet.add(child);
         }
     }
 }