P3811 乘法逆元

传送

乘法逆元：ax ≡ 1 (mod p)，其中x为a的逆元，求模意义下的乘法逆元，通常有一下几种方法：

1.拓展欧几里得（也就是exgcd）

ax ≡ 1 (mod p)

ax-py=1

这就变成解不定方程的问题了，根据拓展欧几里得算法，代码如下（会TLE3个点）（就算开o2优化也没有卵用）

#include<iostream>
#include<cstdio>
using namespace std;
long long n,p;
void exgcd(long long a,long long b,long long &d,long long &x,long long&y)//其中d为a,b的最大公约数
{if(b==){x=;y=;d=a;//当然,exgcd 也可以写成water lift 大佬的有返回值的
}
  else{
      exgcd(b,a%b,d,y,x);
      y-=a/b*x;
  }
}
int main()
{
    cin>>n>>p;
    for(long long i=;i<=n;i++)
    {  long long x,y,d;
        exgcd(i,p,d,x,y);
        cout<<((x/d)%(p/d)+(p/d))%(p/d)<<endl;//防止x为负数
    }
}

2.费马小定理（因为数据保证p为质数）

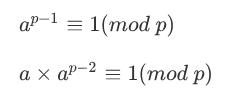
所以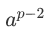即为a的逆元。

n个月过后来补个锅（这玩意用快速幂做）

代码：

#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
int a,p;
int ksm(int a,int b,int p)
{int r=;
   while(b)
   {if(b&)r=r*a%p;
     a=a*a%p;
     b/=;
   }
   return r;
}
int main()
{
    scanf("%d%d",&a,&p);
    cout<<ksm(a,p-,p);
}

不过依旧会TLE

3.说了这么多，终于说到不TLE的解法了

那就是线性递推

这样，就得到了a在模p意义下的逆元

递推式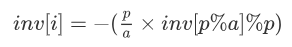 

为了让结果不是负数，递推式就变为 

代码如下

#include<iostream>
#include<cstdio>
using namespace std;
long long n,p,f[];
int main()
{
    scanf("%lld %lld",&n,&p);//要用scanf和printf,不然会超时
    f[]=;f[]=;
    printf("%lld \n",f[]);
    for(long long i=;i<=n;i++)
    {  f[i]=(long long)((p-p/i)*f[p%i])%p;
      printf("%lld \n",f[i]);
    }

}