牛客OI赛制测试赛2

A题:

https://www.nowcoder.com/acm/contest/185/A

链接：https://www.nowcoder.com/acm/contest/185/A
来源：牛客网

题目描述

给出一个二元组（A,B）
求出无序二元组（a,b）使得（a|A，b|B）的组数
无序意思就是(a,b)和(b,a) 算一组.

输入描述:

第一行数据组数 T（1≤T≤10000）
接下来T行，每行两个正整数 A,B（1≤A,B≤10000）

输出描述:

共T行，每行一个结果

输入例子:

1
4 6

输出例子:

-->

示例1

输入

复制

1
4 6

输出

复制

说明

样例解释：
二元组如下：
(1,1)(1,2)(1,3)(1,6)
(2,1)(2,2)(2,3)(2,6)
(4,1)(4,2)(4,3)(4,6)
共12组.
无序二元组如下：
 
(1,1)(1,2)(1,3)(1,6)
(2,2)(2,3)(2,6)
(4,1)(4,2)(4,3)(4,6)
共11组
 
分析: 
     题意很明确了,T组数据,给定两个数,让我们求这两个数的的约数可以组成多少个无序的二元组.
     我们可以这么做: 找出A, B的所有因子数, 然后相乘,再减去重复算的就是答案了. 
 
     即: 答案 = |A| * |B| - |公共因子数| * |公共因子数 + 1| / 2; (从公共因子中选出2个,作为一个二元组, C(2,n) )
 
     然后我们观察数据,发现有T有1e4, 然后A,B也是1e4的,如果A,B直接暴力找的话,那么每次查找约数都是O(sqrt(n))的,
     同时要判除相同的因子个数,如果常数大了,是很容易T的.(反正我的暴力解法是T了的)
 
     有一个结论:  两个数的公约数的个数为这个两个数的最大公约数的约数个数 ---> 即a,b两个数的公约数个数 =  gcd(a,b)的约数个数.
     所以,我们可以预处理出1-10000的所有约数, 然后每次就可以O(1)的计算答案了.然后没了.
 
代码:

#include <cstdio>
#include <cmath>
#include <set>
 
using namespace std;
 
int pre[];
 
int gcd(int a, int b) { return !b ? a : gcd(b, a%b); }
 
int main() {
    int t, i, j, tmp, a, b;
    int res;
    set<int> se;
    for (i=; i<=; ++i) {
        tmp = sqrt(i);
        se.clear();
        for (j=; j<=tmp; ++j) {
            if (i%j==) {
                se.insert(j);
                se.insert(i / j);
            }
        }
        pre[i] = se.size();
    }
    scanf("%d", &t);
    while (t--) {
        scanf("%d%d", &a, &b);
        res = pre[a] * pre[b];
        res -= pre[gcd(a, b)] * (pre[gcd(a, b)]-)/;
        printf("%d\n", res);
    }
 
    return ;
}

-----------------------------------------------------------------------------------------------------------------------------------------这是一条分割线------------------------------------------------------------------------------------------------------------------

B题: 
https://www.nowcoder.com/acm/contest/185/B
链接：https://www.nowcoder.com/acm/contest/185/B
来源：牛客网

题目描述

给出一个 n * n 的邻接矩阵A.

A是一个01矩阵 .

A[i][j]=1表示i号点和j号点之间有长度为1的边直接相连.

求出从 1 号点到 n 号点长度为k的路径的数目.

输入描述:

第1行两个数n,k (20 ≤n ≤ 30,1 ≤ k ≤ 10)
第2行至第n+1行，为一个邻接矩阵

输出描述:

题目中所求的数目

示例1

输入

复制

输出

复制

B题, 原理我还不是很懂,所以不讲. 
所以不如看别人的题解 https://www.nowcoder.com/discuss/104612?type=101&order=1&pos=2&page=1

#include <cstdio>
#include <cstring>
 
using namespace std;
 
typedef long long ll;
 
class Matrix {
public:
    int r, c;
    ll mat[][];
 
    ll *operator [] (int x) { return mat[x]; }
 
    Matrix operator * (const Matrix &a) const {
        Matrix res;
        res.r = r; res.c = a.c;
        int i, j, k;
        for (i=; i<=res.r; ++i) {
            for (j=; j<=res.c; ++j) {
                res[i][j] = ;
                for (k=; k<=c; ++k)
                    res[i][j] += mat[i][k] * a.mat[k][j];
            }
        }
        return res;
    }
 
}m;
 
Matrix pwr(const Matrix &a, int k) {
    Matrix base = a, r;
    int i, j;
    r.r = a.r; r.c = a.c;
    for (i=; i<=r.r; ++i)
        for (j=; j<=r.c; ++j)
            r[i][j] = i==j;
    while (k) {
        if (k & ) r = r * base;
        base = base * base;
        k >>= ;
    }
    return r;
}
 
int main()
{
    int n, k, i, j;
    scanf("%d%d", &n, &k);
    for (i=; i<=n; ++i)
        for (j=; j<=n; ++j)
            scanf("%d", &m[i][j]);
    m.r = n; m.c = n;
    m = pwr(m, k);
    printf("%lld\n", m[][n]);
    return ;
}

C题:

https://www.nowcoder.com/acm/contest/185/C

链接：https://www.nowcoder.com/acm/contest/185/C
来源：牛客网

题目描述

给出一个数列 A，求出一个数列B.

其中B_i表示数列A中 A_i右边第一个比 A_i 大的数的下标(从1开始计数),没有找到这一个下标 Bi 就为0

输出数列B

输入描述:

第一行1个数字 n (n ≤ 10000)

第二行n个数字第 i 个数字为 A_i (0 ≤ A_i≤ 1000000000)

输出描述:

一共一行，第 i 个数和第 i+1 个数中间用空格隔开.

输入例子:

6
3 2 6 1 1 2

输出例子:

3 3 0 6 6 0

-->

示例1

输入

6
3 2 6 1 1 2

输出

3 3 0 6 6 0
 
分析: 题意很简单,在数列中从左往右,找到第一个比当前数大的数的下标,如果没有,则为0.
     我们发现数据是1e4的...暴力貌似也就5e7....也许可以吧= =.我没暴力.
     暴力是正着扫的,复杂度是O(n^2) 我们不妨倒着考虑.
     1. 从最后一个数开始,往前找,如果找到一个比当前数A小的B, 那么B的答案应该是A的下标.
                            如果找到一个比当前数A大的C, 那么C的答案应该由当前数A往右的数来决定,如果有比C大的那么C的答案不为0,否则为0;
     2. 基于这个想法,我们发现可以用一个队列来模拟这个过程:   
        1). 从最后一个数开始,往前找,如果找到一个比当前数A(队首元素)小的B, 那么B的答案应该是A的下标. 同时B插到队首,
                           如果找到一个比队首元素大的数C, 那么队首元素出队,直到找到一个比C大的数,或者队空. 
                                                      如果找到比C大的数, 那么C的答案更新为下标, 同时C插到队首,
                                                      如果队空了, 那么C的答案为0, 同时C插到队首,
        2). 重复这个过程,直到遍历完整个数组,答案就更新完毕了.
    重点是想想,为什么要把更新元素插入到队首, 想想.
    这个也就是单调队列(队列里的元素是单调的.   优先队列里的元素也是单调的,不过有所不同.我暂时也讲不清,大概单调队列我也只会这种水题,,,)

#include <cstdio>
#include <queue>
 
using namespace std;
 
int date[];
int ans[];
struct nobe {
    int val;
    int id;
    nobe () { }
    nobe (int vv, int ii) : val(vv), id(ii) { }
};
 
deque<nobe> dq;
 
int main()
{
    int n, i;
    scanf("%d", &n);
    for (i=; i<=n; ++i) scanf("%d", date+i);
    for (i=n; i; --i) {
        if (dq.empty()) dq.push_front(nobe(date[i], i));
        else if (dq.front().val > date[i]){
            ans[i] = dq.front().id;
            dq.push_front(nobe(date[i], i));
        } else {
            while (!dq.empty() && dq.front().val <= date[i])
                dq.pop_front();
            i++;
        }
    }
    printf("%d", ans[]);
    for (i=; i<=n; ++i) printf(" %d", ans[i]);
    printf("\n");
    return ;
}

D题:

链接：https://www.nowcoder.com/acm/contest/185/D

题目描述

Johnson和Nancy要在星光下吃晚餐。这是一件很浪漫的事情。

为了增加星光晚餐那浪漫的氛围，他拿出了一个神奇的魔法棒，并且可以按照一定的规则，改变天上星星的亮暗。

Johnson想考考Nancy，在他挥动魔法棒后，会有多少颗星星依旧闪耀在天空。他知道，Nancy一定会一口说出答案。

Nancy当然知道怎么做啦，但她想考考你！

Johnson先将天上n个星星排成一排，起初它们都是暗的。

他告诉他的妹子，他将挥动n次魔法棒，第i次挥动会将编号为i的正整数倍的星星的亮暗反转，即亮的星星转暗，暗的星星转亮。

Johnson想问Nancy，最终会有多少个星星依旧闪亮在天空。

输入描述:

一个整数n，含义请见题目描述。

输出描述:

一个整数ans，即n次操作后会有多少个星星依旧闪亮。

输入

输出

输入

输出

备注:

对于60%的数据：n≤2×10

⁶

对于100%的数据：n≤10

¹⁸

分析: 题目给你n个标号为1...n的初始为暗星星,然后你要开关n次, 第i次关闭标号为i的倍数的星星,问最后有多少个亮着的星星.
范围: 1e18, 简单, 肯定暴力. 才怪. 所以应该是有公式或者规律可以O(1)算的.
我们发现,对于一个星星,如果开关了偶数次,那么状态不变,最后还是暗的. 如果开关了奇数次,那么最后就亮的.
所以我们的问题转化为: 被开关了奇数次的星星个数.
第i次关的是i的倍数的星星, 我们可以反过来考虑, 对于一个标号为k的星星来说,它会在x次被关闭,当且仅当x|k.(x整除k), 即x是k的因子.
所以,我们的问题又转化为了: 求1...n以内 因子个数是奇数的数的个数了.
我们发现, 知道,只有平方数的因子个数是奇数个,其他的都是偶数个.(想想.)
所以,问题就是: 求1...n以内,有多少个平方数.
答案是sqrt(n)向下取整. (想想.)

#include <cstdio>
#include <cmath>
 
int main()
{
    long long n, res;
    scanf("%lld", &n);
    res = sqrt(n);
    printf("%lld\n", res);
    return ;
}

E题:

链接：https://www.nowcoder.com/acm/contest/185/E

题目描述

给定括号长度N，给出一串括号（只包含小括号），计算出最少的交换（两两交换）次数，使整个括号序列匹配。
我们认为一个括号匹配，即对任意一个')'，在其左侧都有一个'('与它匹配，且他们形成一一映射关系。

输入描述:

第一行：整数N，表示括号序列长度
第二行：一个字符串，表示括号

输出描述:

一个整数，表示最少的交换次数

输入

6
(()))(

输出

输入

6
)))(((

输出

2
分析: 题意就是给一个括号串,问最小交换多少次,可以让括号串括号都可以匹配.
     1. 很自然的想法, 如果已经匹配了的括号,那么我们肯定不需要交换它们了. 
     2. 如果我们删除本来就匹配了的括号,那么剩下的括号一定是))))))))))))))(((((((((((这种形式了.
     3. 对于这种剩下的括号,如果是有偶数对,那么我们贪心的交换,一次都可以匹配2对, 而且这便是最优的了.
     4. 如果剩下奇数对,我们最后一对也需要交换一次.
        所以,我们交换次数 =  (总括号对数 - 原先就匹配了的对数 + 1 ) / 2  即: (未匹配括号对数+1) / 2
 
     然后,我们怎么求解已经匹配了的括号对数呢? 很简单,我们直接用一个栈来模拟. 遇到左括号入栈,遇到右括号,如果栈有元素出栈,匹配数++,如果栈为空,继续扫下一个字符.

#include <bits/stdc++.h>
using namespace std;
char str[];
int main()
{
    int n, i, cnt = ;
    scanf("%d%s", &n, str);
    stack<char> st;
    for (i=; i<n; ++i)
        if (str[i] == '(')    st.push(str[i]);
        else if (!st.empty()) st.pop(),cnt++;
    printf("%d\n", (n/ - cnt + ) / );
    return ;
}

F题:

链接：https://www.nowcoder.com/acm/contest/185/F

题目描述

输入一个整数X，求一个整数N，使得N!恰好大于X^X。

输入描述:

第一行：一个整数X

输出描述:

第一行：一个整数N

输入

输出

备注:

每个测试点所对应的X满足：
 
第i个测试点输入的值为第i-1个测试点输入的值乘以10再加上7。
 
特别的，第一个测试点所输入的值为7。
 
提示：数据共有10组。

分析: 要找到满足N! > X^X , 我们发现X最后会很大, 计算用高精度也肯定爆,所以我们考虑用数学方法. 
     我们可以两边取一个对数  那么就有 lgN! > XlgX  然后根据题意,X最多1e9 那么,我们就可以用二分,来枚举N了.
    那么lgN!应该怎么算呢?  N!有一个近似的公式: 斯特林公式:

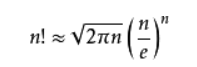然后,我们就有 lg(sqrt(2 * PI * n)) + n * lg(n / e) > X lgX ,然后就可以愉快的二分了, 当然要注意精度问题.(...我不懂精度)

#include <iostream>
#include <cmath>
 
using namespace std;
 
const double PI = acos(-1.0);
const double e  = exp(1.0);
const double eps = 1e-;
int main()
{
//  freopen("E:\\input.txt", "r", stdin);
    long double x;
 
    while (cin >> x) {
        x = x * log(x);
        long double left = 0.0, right = 9999999999.0;
        while (right - left > eps) {
            long double n = (left + right) / 2.0;
            long double jc = log( * PI * n) / 2.0  + n * log(n / e);
            if (jc > x) {
                right = n;
            } else {
                left = n;
            }
        }
        cout << (long long)left +  << endl;
    }
 
    return ;
}
/*
10
94
892
8640
84657
834966
8267019
82052137
815725636
8118965902
*/