决策树算法——ID3

决策树算法是一种有监督的分类学习算法。利用经验数据建立最优分类树，再用分类树预测未知数据。

例子：利用学生上课与作业状态预测考试成绩。

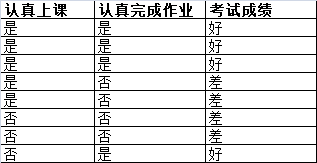
上述例子包含两个可以观测的属性：上课是否认真，作业是否认真，并以此预测考试成绩。针对经验数据，我们可以建立两种分类树

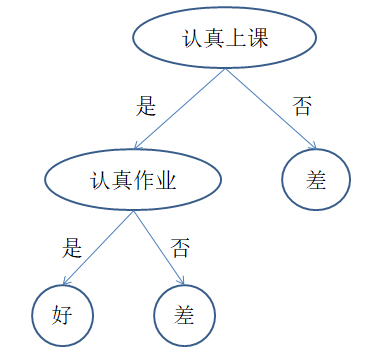
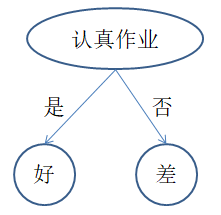
两棵树都能对经验数据正确分类，实际上第二棵树更好，原因是什么呢？在此，我们介绍ID3分类算法。

1、信息熵

例如，我们想要获取球队比赛胜负的信息：中国队vs巴西队、中国队vs沙特队。

哪场比赛信息量高？答案是中国队vs沙特队。原因是中国队vs沙特队输赢的确定性小于中国队vs巴西队输赢的确定性。

假设样本集合是D，其中第k类样本所占的比例为pk，则D的信息熵为

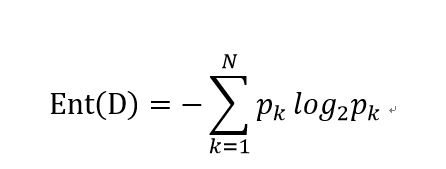
假设中国队vs巴西队输的概率为80%，则信息量Ent = -0.8 * log2(0.8) - 0.2 * log2(0.2) = 0.722。

假设中国队vs沙特队输的概率为50%，则信息量Ent = -0.5 * log2(0.5) - 0.5 * log2(0.5) = 1。

我们可以看出来，不确定性越高的场景包含越多的信息量。

2、信息增益

实际应用中，单独使用信息熵的情况比较少，往往使用信息熵的增益来指导工作。

基于信息熵，我们可以对某个属性a定义"信息增益"

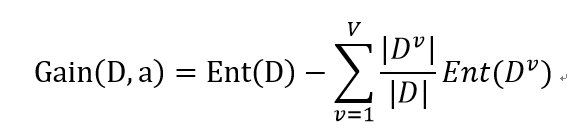
其中，a属性有V个可能取值，而D中在属性a上取值为的样本记为Dv。

比如我们买足彩竞猜两支球队的输赢，我们可以获得两个消息中的一个：比赛球队是哪两个球队，比赛日期是哪一天。你愿意获取哪一个消息？相信大部分人都会选择前一个消息。原因很简单，前一个消息对于我们预测输赢的帮助高于后一个消息。

在我们没有任何额外信息的情况下，两支球队的输赢为50%。但是当我们知道了球队名称后，我们可以根据他们的FIFA排名来预测输赢。FIFA排名高的赢得概率更高。仅仅知道比赛日期可能对于我们的预测没有太大帮助。

比如我们知道了是中国队vs巴西队的比赛，则信息增量为1-0.722 = 0.278。

3、ID3算法原理

每次分类，我们选取信息增益最大的属性进行分类，然后进行递归分类。

对于文章开始的例子，初始信息熵为Ent = -0.5 * log2(0.5) - 0.5 * log2(0.5) = 1。

选择认真上课属性后，信息熵Ent(认真上课)  = -5/8 * ((3/5 * log2(3/5) - 2/5 * log2(2/5)) - 3/8 * ((1/3 * log2(1/3) - 2/3 * log2(2/3)) = 0.951，信息增益为0.049。

选择认真作业属性后，信息熵Ent(认真作业)  = -4/8 * ((1 * log2(1) - 0 * log2(0)) - 4/8 * ((1 * log2(1) - 0 * log2(0)) = 0，信息增益为1。

所以选择认真作业属性更优。

4、实例

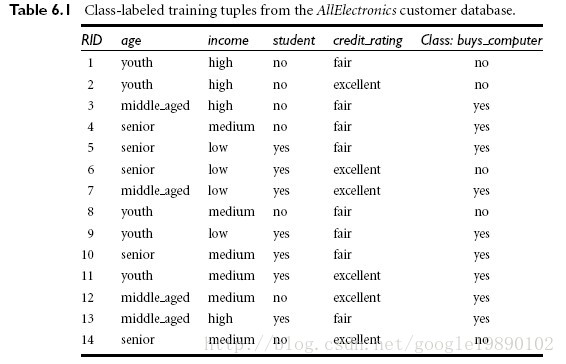
根据年龄，身份，收入，信用预测买电脑的情况。java代码如下

package com.coshaho.learn.detree;

import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;

/**
 *
 * ID3Tree.java Create on 2018年6月19日 上午12:29:06
 *
 * 类功能说明:   ID3 决策树算法
 *
 * Copyright: Copyright(c) 2013
 * Company: COSHAHO
 * @Version 1.0
 * @Author coshaho
 */
public class ID3Tree
{
    public void createTree(String[] feature, int[][] data)
    {
        Node root = new Node();
        root.setParent(null);
        root.setFeature("root");
        root.setValue(-1);
        root.setLevel(0);
        bestFit(feature, data, root, 0);
        System.out.print(root);
    }

    /**
     * 选择最优属性（获得信息量最大的属性）
     * @author coshaho
     * @param feature
     * @param data
     * @param parent
     * @param level
     */
    public void bestFit(String[] feature, int[][] data, Node parent, int level)
    {
        if(!validateData(data))
        {
            Node me = new Node();
            me.setLevel(level + 1);
            me.setFeature("class");
            me.setParent(parent);
            me.setValue(data[0][data[0].length - 1]);
            parent.getChildren().add(me);
            return;
        }

        int m = data.length;
        int n = data[0].length;
        int featureNum = n - 1;

        // 计算当前信息量
        double oldEntropy = calEntropy(data);
        double gainEntropy = -1d;
        int bestFeature = 0;
        Map<Integer, int[][]> nextData = null;
        for(int i = 0; i < featureNum; i++)
        {
            double newEntropy = 0.0d;
            Map<Integer, int[][]> splitData = splitData(data, i);

            // 按照某属性分类后的信息量
            for(Map.Entry<Integer, int[][]> entry : splitData.entrySet())
            {
                double entropy = calEntropy(entry.getValue());
                newEntropy = newEntropy + entropy * entry.getValue().length / m;
            }

            // 选取信息量获取最大的属性分类
            if(oldEntropy - newEntropy > gainEntropy)
            {
                gainEntropy = oldEntropy - newEntropy;
                bestFeature = i;
                nextData = splitData;
            }
        }

        String[] nextFeature = removeBestFeature(feature, bestFeature);

        // 递归分解
        for(Map.Entry<Integer, int[][]> entry : nextData.entrySet())
        {
            Node me = new Node();
            me.setFeature(feature[bestFeature]);
            me.setParent(parent);
            me.setValue(entry.getKey());
            me.setLevel(level + 1);
            parent.getChildren().add(me);
            bestFit(nextFeature, entry.getValue(), me, level + 1);
        }

    }

    /**
     * 移除已经分类的属性
     * @author coshaho
     * @param feature
     * @param index
     * @return
     */
    private String[] removeBestFeature(String[] feature, int index)
    {
        String[] result = new String[feature.length - 1];
        boolean flag = true;
        for(int j = 0; j < feature.length; j++)
        {
            if(index == j)
            {
                flag = false;
                continue;
            }
            if(flag)
            {
                result[j] = feature[j];
            }
            else
            {
                result[j - 1] = feature[j];
            }
        }

        return result;
    }

    /**
     * 计算信息熵
     * Entropy = -sigma(u * log2(u))
     * @author coshaho
     * @param data
     * @return
     */
    private double calEntropy(int[][] data)
    {
        int m = data.length;
        int n = data[0].length;

        Map<Integer, Integer> map = new HashMap<Integer, Integer>();
        for(int i = 0; i < m; i++)
        {
            map.put(data[i][n-1], null == map.get(data[i][n-1]) ? 1 : map.get(data[i][n-1]) + 1);
        }

        double result = 0.0d;
        for(Map.Entry<Integer, Integer> entry : map.entrySet())
        {
            result = result - (double)entry.getValue() / m * Math.log((double)entry.getValue() / m) / Math.log(2);
        }
        return result;
    }

    /**
     * 按照属性index进行数据聚类
     * @author coshaho
     * @param data
     * @param index
     * @return
     */
    private Map<Integer, int[][]> splitData(int[][] data, int index)
    {
        int m = data.length;
        int n = data[0].length;

        // 数据划分：删除某列属性值并按照这列属性划分数据
        Map<Integer, List<int[]>> map = new HashMap<Integer, List<int[]>>();
        for(int i = 0; i < m; i++)
        {
            int key = data[i][index];
            int[] v = new int[n - 1];
            boolean flag = true;
            for(int j = 0; j < n; j++)
            {
                if(index == j)
                {
                    flag = false;
                    continue;
                }
                if(flag)
                {
                    v[j] = data[i][j];
                }
                else
                {
                    v[j - 1] = data[i][j];
                }
            }

            if(map.containsKey(key))
            {
                map.get(key).add(v);
            }
            else
            {
                List<int[]> list = new ArrayList<int[]>();
                list.add(v);
                map.put(key, list);
            }
        }

        // 数据格式转换
        Map<Integer, int[][]> result = new HashMap<Integer, int[][]>();
        for(Map.Entry<Integer, List<int[]>> entry : map.entrySet())
        {
            List<int[]> v = entry.getValue();
            int[][] value = new int[v.size()][];
            v.toArray(value);
            result.put(entry.getKey(), value);
        }

        return result;
    }

    /**
     * 数据校验
     * @author coshaho
     * @param data
     * @return
     */
    private boolean validateData(int[][] data)
    {
        if(1 == data.length || 1 == data[0].length)
        {
            return false;
        }

        int m = data.length;
        int n = data[0].length;

        int classOne = 1;
        for(int i = 1; i < m; i++)
        {
            if(data[i][n - 1] == data[0][n - 1])
            {
                classOne++;
            }
        }

        if(m == classOne)
        {
            return false;
        }

        return true;
    }

    public static class Node
    {
        private Node parent;

        private List<Node> children = new ArrayList<Node>();

        private int value;

        private String feature;

        private int level;

        public int getLevel() {
            return level;
        }

        public void setLevel(int level) {
            this.level = level;
        }

        public Node getParent() {
            return parent;
        }

        public void setParent(Node parent) {
            this.parent = parent;
        }

        public List<Node> getChildren() {
            return children;
        }

        public void setChildren(List<Node> children) {
            this.children = children;
        }

        public int getValue() {
            return value;
        }

        public void setValue(int value) {
            this.value = value;
        }

        public String getFeature() {
            return feature;
        }

        public void setFeature(String feature) {
            this.feature = feature;
        }

        public String toString()
        {
            String result = blank() + feature + ":" + value + "\n";
            for(Node node : children)
            {
                result = result + node.toString();
            }

            return result;
        }

        private String blank()
        {
            StringBuffer sb = new StringBuffer();
            for(int i = 0; i < level; i++)
            {
                sb.append("--");
            }
            return sb.toString();
        }
    }

    public static void main(String[] args)
    {
        int[][] data = {{0,2,0,0,0},
                {0,2,0,1,0},
                {1,2,0,0,1},
                {2,1,0,0,1},
                {2,0,1,0,1},
                {2,0,1,1,0},
                {1,0,1,1,1},
                {0,1,0,0,0},
                {0,0,1,0,1},
                {2,1,1,0,1},
                {0,1,1,1,1},
                {1,1,0,1,1},
                {1,2,1,0,1},
                {2,1,0,1,0}};
        String[] feature = {"age", "income", "student", "credit", "class"};

        new ID3Tree().createTree(feature, data);
    }
}

运行结果

root:-1
--age:0
----student:0
------class:0
----student:1
------class:1
--age:1
----class:1
--age:2
----credit:0
------class:1
----credit:1
------class:0