UVALive 7455 Linear Ecosystem （高斯消元）

Linear Ecosystem

题目链接：

http://acm.hust.edu.cn/vjudge/contest/127401#problem/B

Description

http://7xjob4.com1.z0.glb.clouddn.com/99b0fe905e5bd89a24c882832c93cc09

Input

The first line of the input file contains an integer, n, which is the number of ecosystems. For each case,
the first line contains the integer k which is the number of comorgs. Followed by k lines, where the i-th
line contains, αi,1, αi,2, . . . , αi,k, the coefficients of the transition equation for ci.

Output

For each test case, output ‘1’ if the ecosystem is potentially stable, otherwise output ‘0’. Output only
5 answers per line. There should be a blank space between any two output answers.

Sample Input

6
2
4 -2
-6 5
2
2 2
0 0
3
0.3 0.2 0.5
0.4 0.4 0.2
0 0.8 0.2
3
0.3 0.2 0.5
0 0 0
0 0.8 0.2
2
4 2.0
-6 5
2
1 0
0 1

Sample Output

1 0 1 0 0
1


##题意：

对一个k元向量, 每次左乘一个k*k的矩阵得到新的向量.
问经过一定次数的左乘后，能否使得该向量不再变化. (同时要求此时向量非零)


##题解：

设初始向量为A，矩阵为P.
由于每次矩阵P都是左乘A, 那么可以把若干个P合并. 则题目的条件是：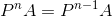
化简为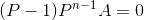：  由于要求 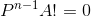 所以 P-1 必须不可逆.
可以直接用高斯消元求P-1的秩，判断是否可逆（满秩即可逆）.


##代码：
``` cpp
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define LL long long
#define eps 1e-6
#define maxn 50
#define mod 100000007
#define inf 0x3f3f3f3f
#define mid(a,b) ((a+b)>>1)
#define IN freopen("in.txt","r",stdin);
using namespace std;

double a[maxn][maxn],x[maxn];

int equ,var;

int Gauss()

{

int i,j,k,col,max_r;

for(k=0,col=0;k<equ&&col<var;k++,col++){

max_r = k;

for(i=k+1;i<equ;i++)

if(fabs(a[i][col])>fabs(a[max_r][col]))

max_r = i;

if(fabs(a[max_r][col])<eps) return 0; //无解,有自由变元

if(k != max_r){

for(j=col;j<var;j++)

swap(a[k][j],a[max_r][j]);

swap(x[k],x[max_r]);

}

x[k]/=a[k][col];

for(j=col+1;j<var;j++)a[k][j]/=a[k][col];

a[k][col] = 1;

for(i=0;i<equ;i++)

if(i!=k){

x[i] -= x[k]a[i][k];

for(j=col+1;j<var;j++)a[i][j]-=a[k][j]a[i][col];

a[i][col]=0;

}

}

return 1;

}

vector ans;

int main(int argc, char const *argv[])

{

//IN;

int t; cin >> t;
while(t--)
{
    memset(a, 0, sizeof(a));
    cin >> equ; var = equ;
    for(int i=0; i<equ; i++) {
        for(int j=0; j<var; j++) {
            cin >> a[i][j];
        }
        a[i][i] -= 1.0;   /* P - 1 */
    }

    if(Gauss()) ans.push_back(0);
    else ans.push_back(1);
}

for(int i=0; i<ans.size(); i++) {
    printf("%d%c", ans[i], (i%5==4||i==ans.size()-1)?'\n':' ');
}

return 0;

}