【UE4】GAMES101 图形学作业1：mvp 模型、视图、投影变换

总览

• 到目前为止，我们已经学习了如何使用矩阵变换来排列二维或三维空间中的对象。所以现在是时候通过实现一些简单的变换矩阵来获得一些实际经验了。在接下来的三次作业中，我们将要求你去模拟一个基于CPU 的光栅化渲染器的简化版本。
• 本次作业的任务是填写一个旋转矩阵和一个透视投影矩阵。给定三维下三个点v0(2.0, 0.0,−2.0), v1(0.0, 2.0,−2.0), v2(−2.0, 0.0,−2.0), 你需要将这三个点的坐标变换为屏幕坐标并在屏幕上绘制出对应的线框三角形。简而言之，我们需要进行模型、视图、投影、视口等变换来将三角形显示在屏幕上
• get_model_matrix(float rotation_angle)
  
  逐个元素地构建模型变换矩阵并返回该矩阵。在此函数中，你只需要实现三维中绕 z 轴旋转的变换矩阵，而不用处理平移与缩放。
• get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar)
  
  使用给定的参数逐个元素地构建透视投影矩阵并返回该矩阵。
• 当你在上述函数中正确地构建了模型与投影矩阵，光栅化器会创建一个窗口显示出线框三角形。由于光栅化器是逐帧渲染与绘制的，所以你可以使用A 和D 键去将该三角形绕z 轴旋转

基础与提高

• [5 分] 正确构建模型矩阵。
• [5 分] 正确构建透视投影矩阵。
• [10 分] 你的代码可以在现有框架下正确运行，并能看到变换后的三角形。
• [10 分] 当按A 键与D 键时，三角形能正确旋转。或者正确使用命令行得到旋转结果图像。
• [提高项5 分] 在main.cpp 中构造一个函数，该函数的作用是得到绕任意过原点的轴的旋转变换矩阵。
  
  Eigen::Matrix4f get_rotation(Vector3f axis, float angle)

实现

• 投影变换矩阵

  

• 模型任意轴旋转

  

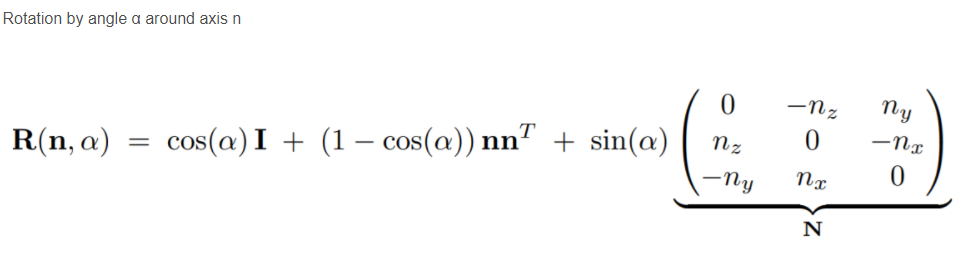
代码

创建 AActor 派生类 AActor_Assignmen1

• AActor_Assignmen1.h

  UCLASS()
  class GAMES101_API AActor_Assignmen1 : public AActor
  {
  	GENERATED_BODY()
  
  public:
  	// Sets default values for this actor's properties
  	AActor_Assignmen1();
  
  protected:
  	// Called when the game starts or when spawned
  	virtual void BeginPlay() override;
  
  public:
  	// Called every frame
  	virtual void Tick(float DeltaTime) override;
  	void DrawTriangleIn3D();
  
  	//主要函数
  	FMatrix get_view_matrix(FVector eye_pos);
  	FMatrix get_model_matrix(float rotation_angle);
  	FMatrix get_model_matrix_anyAxis(FVector axis, float angle);
  	FMatrix get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar);
  
  	void RasterizerDraw();
  
  public:
  	UPROPERTY(EditAnywhere, BlueprintReadWrite,  meta = (MakeEditWidget))
  	FTransform ponitA;
  	UPROPERTY(EditAnywhere,BlueprintReadWrite,  meta = (MakeEditWidget))
  	FTransform ponitB;
  	UPROPERTY(EditAnywhere,BlueprintReadWrite,  meta = (MakeEditWidget))
  	FTransform ponitC;
  
  	UPROPERTY()
  	USceneComponent* root;
  
  	UPROPERTY()
  	TArray<FVector> Points;
  	int32 width, height;
  	FVector eye_loc;
  	float angle;
  
  	FMatrix modelMatrix;
  	FMatrix viewMatrix;
  	FMatrix projectionMatrix;
  };
  

• AActor_Assignmen1.cpp

  #include "Actor_Assignmen1.h"
  #include "Kismet/KismetSystemLibrary.h"
  #include "Kismet/KismetMathLibrary.h"
  #include "GameFramework/HUD.h"
  #include "Kismet/GameplayStatics.h"
  #include "MyHUD.h"
  
  // Sets default values
  AActor_Assignmen1::AActor_Assignmen1()
  {
  	// Set this actor to call Tick() every frame.  You can turn this off to improve performance if you don't need it.
  	PrimaryActorTick.bCanEverTick = true;
  	root = CreateDefaultSubobject<USceneComponent>("root");
  	SetRootComponent(root);
  
  	// 三个点v0(2.0, 0.0,−2.0), v1(0.0, 2.0,−2.0), v2(−2.0, 0.0,−2.0),
  	Points.Add(FVector(2.0f, 0, -2.0f));
  	Points.Add(FVector(0, 2.0f,-2.0f));
  	Points.Add(FVector(-2.0f, 0,-2.0f));
  
  	// 初始化
  	width = height = 700;
  	eye_loc = FVector(0, 0, 5);
  	angle = 0;
  
  	modelMatrix.SetIdentity();
  	viewMatrix.SetIdentity();
  	projectionMatrix.SetIdentity();
  
  	ponitA.SetTranslation(Points[0]);
  	ponitB.SetTranslation(Points[1]);
  	ponitC.SetTranslation(Points[2]);
  }
  
  // Called every frame
  void AActor_Assignmen1::Tick(float DeltaTime)
  {
  	Super::Tick(DeltaTime);
  	FVector2D ViewportSize;
  	GetWorld()->GetGameViewport()->GetViewportSize(ViewportSize);
  	width = height = ViewportSize.X / 2;
  
  	// 绕z轴
  	//modelMatrix = get_model_matrix(angle);
  
  	//绕任意轴
  	modelMatrix = get_model_matrix_anyAxis(FVector(0, 0, 5), angle);
  	viewMatrix = get_view_matrix(eye_loc);
  	projectionMatrix = get_projection_matrix(45, 1, 0.1, 50);
  
  	RasterizerDraw();
  	angle += 0.5;
  	root->SetWorldRotation(FRotator(0, angle, 0));
  }
  
  FMatrix AActor_Assignmen1::get_view_matrix(FVector eye_pos)
  {
  	FMatrix view = FMatrix::Identity;
  
  	FMatrix translate = FMatrix(
  		FPlane(1, 0, 0, -eye_pos.X),
  		FPlane(0, 1, 0, -eye_pos.Y),
  		FPlane(0, 0, 1, -eye_pos.Z),
  		FPlane(0, 0, 0, 1));
  
  	view = translate * view;
  	return view;
  }
  
  // 绕 Z 轴旋转
  FMatrix AActor_Assignmen1::get_model_matrix(float rotation_angle)
  {
  	FMatrix model = FMatrix::Identity;
  
  	// TODO: Implement this function
  	// Create the model matrix for rotating the triangle around the Z axis.
  	// Then return it.
  	float fcos = UKismetMathLibrary::DegCos(rotation_angle);
  	float fsin = UKismetMathLibrary::DegSin(rotation_angle);
  	FMatrix rotate = FMatrix(
  		FPlane(fcos, -fsin, 0, 0),
  		FPlane(fsin,  fcos, 0, 0),
  		FPlane(	  0,     0, 1, 0),
  		FPlane(	  0,     0, 0, 1));
  
  	model = rotate * model;
  
  	return model;
  }
  
  // 任意轴旋转
  FMatrix AActor_Assignmen1::get_model_matrix_anyAxis(FVector axis, float rotation_angle)
  {
  	FMatrix model = FMatrix::Identity;
  
  	axis.Normalize(0.0001);
  	FMatrix N = FMatrix(
  		FPlane(0, -axis.Z, axis.Y, 0),
  		FPlane(axis.Z, 0, -axis.X, 0),
  		FPlane(-axis.Y, axis.X, 0, 0),
  		FPlane(0, 0, 0, 0));
  
  	FMatrix rotate4f = FMatrix::Identity * UKismetMathLibrary::DegCos(rotation_angle);
  
  	// nnt = axis x axis的转置
  	FMatrix nnT = FMatrix(
  		FPlane(axis.X*axis.X, axis.X*axis.Y, axis.X*axis.Z, 0),
  		FPlane(axis.Y*axis.X, axis.Y*axis.Y, axis.Y*axis.Z, 0),
  		FPlane(axis.Z*axis.X, axis.Z*axis.Y, axis.Z*axis.Z, 0),
  		FPlane(0, 0, 0, 0));
  
  	rotate4f +=  nnT * (1 - UKismetMathLibrary::DegCos(rotation_angle));
  
  	rotate4f += N * UKismetMathLibrary::DegSin(rotation_angle);
  
  	rotate4f.M[3][3] = 1;
  	model = rotate4f * model;
  	return model;
  }
  
  FMatrix AActor_Assignmen1::get_projection_matrix(float eye_fov, float aspect_ratio, float zNear, float zFar)
  {
  	// Students will implement this function
  	FMatrix projection = FMatrix::Identity;
  
  	float t = zNear * UKismetMathLibrary::DegTan(eye_fov / 2);
  	float b = -t;
  	float r = t * aspect_ratio;
  	float l = -r;
  
  	FMatrix translate = FMatrix(
  		FPlane(2 * zNear / (r - l), 0, -(r + l) / (r - l), 0),
  		FPlane(0, 2 * zNear / (t - b), -(t + b) / (t - b), 0),
  		FPlane(0, 0, -(zNear + zFar) / (zNear - zFar), 2 * zNear * zFar / (zNear - zFar)),
  		FPlane(0, 0, 1, 0));
  	projection = translate * projection;
  
  	return projection;
  }
  
  void AActor_Assignmen1::RasterizerDraw()
  {
  	FMatrix mvp = projectionMatrix * viewMatrix * modelMatrix;
  
  	float f1 = (100 - 0.1) / 2.0;
  	float f2 = (100 + 0.1) / 2.0;
  	TArray<FVector4> v;
  	for (FVector& p : Points) {
  		v.Add(mvp.GetTransposed().TransformFVector4(FVector4(p.X, p.Y, p.Z, 1.0f)));
  	}
  
  	for (FVector4& vert : v) {
  		vert *= 1/vert.W;
  		vert.X = 0.5 * width * (vert.X + 1.0);
  		vert.Y = 0.5 * height * (vert.Y + 1.0);
  		vert.Z = vert.Z * f1 + f2;
  	}
  
  	TArray<FVector> triangleVerts;
  	for (FVector4& vert : v) {
  		triangleVerts.Add(UKismetMathLibrary::Conv_Vector4ToVector(vert));
  	}
  
  	// 调用AHUD 屏幕绘制函数
  	AMyHUD* myHUD = Cast<AMyHUD>(UGameplayStatics::GetPlayerController(GetWorld(), 0)->GetHUD());
  	if (myHUD) {
  		myHUD->rasterize_wireframe(triangleVerts);
  	}
  	/*
  	UKismetSystemLibrary::PrintString(GetWorld(), triangleVerts[0].ToString());
  	UKismetSystemLibrary::PrintString(GetWorld(), triangleVerts[1].ToString());
  	UKismetSystemLibrary::PrintString(GetWorld(), triangleVerts[2].ToString());
  	UKismetSystemLibrary::PrintString(GetWorld(), TEXT("----------"));
  	*/
  }
  
  // 场景里的绘线
  void AActor_Assignmen1::DrawTriangleIn3D() {
  	UKismetSystemLibrary::DrawDebugLine(GetWorld(), Points[0], Points[1], FLinearColor::Green, 0.02f, .2f);
  	UKismetSystemLibrary::DrawDebugLine(GetWorld(), Points[1], Points[2], FLinearColor::Green, 0.02f, .2f);
  	UKismetSystemLibrary::DrawDebugLine(GetWorld(), Points[2], Points[0], FLinearColor::Green, 0.02f, .2f);
  }
  

• 创建蓝图派生类，添加面片
  
  

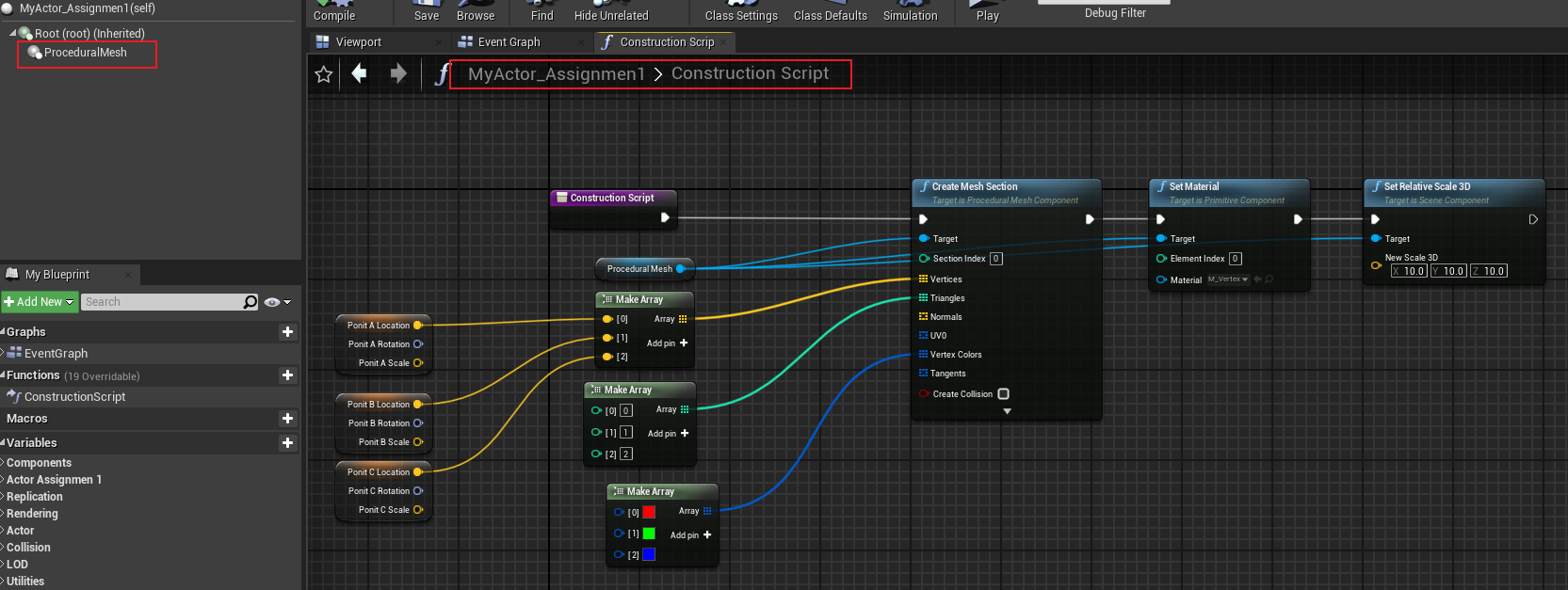
创建 AHUD 派生类 AMyHUD

自创建gamemode 并指定HUD，用于绘制屏幕上的线段

• MyHUD.h

  UCLASS()
  class GAMES101_API AMyHUD : public AHUD
  {
  	GENERATED_BODY()
  
  public:
  	virtual void DrawHUD() override;
  	// 重载用于绘制
  	void rasterize_wireframe(TArray<FVector>& t);
  	// 存储三角形的三个点
  	TArray<FVector> TriangleVerts;
  };
  

• MyHUD.cpp

  void AMyHUD::DrawHUD()
  {
  	Super::DrawHUD();
  	if (TriangleVerts.IsValidIndex(0)) {
  		DrawLine(TriangleVerts[0].X, TriangleVerts[0].Y, TriangleVerts[1].X, TriangleVerts[1].Y,FLinearColor::Red);
  		DrawLine(TriangleVerts[1].X, TriangleVerts[1].Y, TriangleVerts[2].X, TriangleVerts[2].Y,FLinearColor::Red);
  		DrawLine(TriangleVerts[2].X, TriangleVerts[2].Y, TriangleVerts[0].X, TriangleVerts[0].Y,FLinearColor::Red);
  	}
  }
  
  void AMyHUD::rasterize_wireframe(TArray<FVector>& t)
  {
  	TriangleVerts = t;
  }
  

效果