LeetCode---42. 接雨水 (hard)

题目：42. 接雨水

给定 n 个非负整数表示每个宽度为 1 的柱子的高度图，计算按此排列的柱子，下雨之后能接多少雨水。

示例：

输入：height = [0,1,0,2,1,0,1,3,2,1,2,1]

输出：6

解释：上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图，在这种情况下，可以接 6 个单位的雨水（蓝色部分表示雨水）。

第一种解法：暴力破解，一列一列算

思路

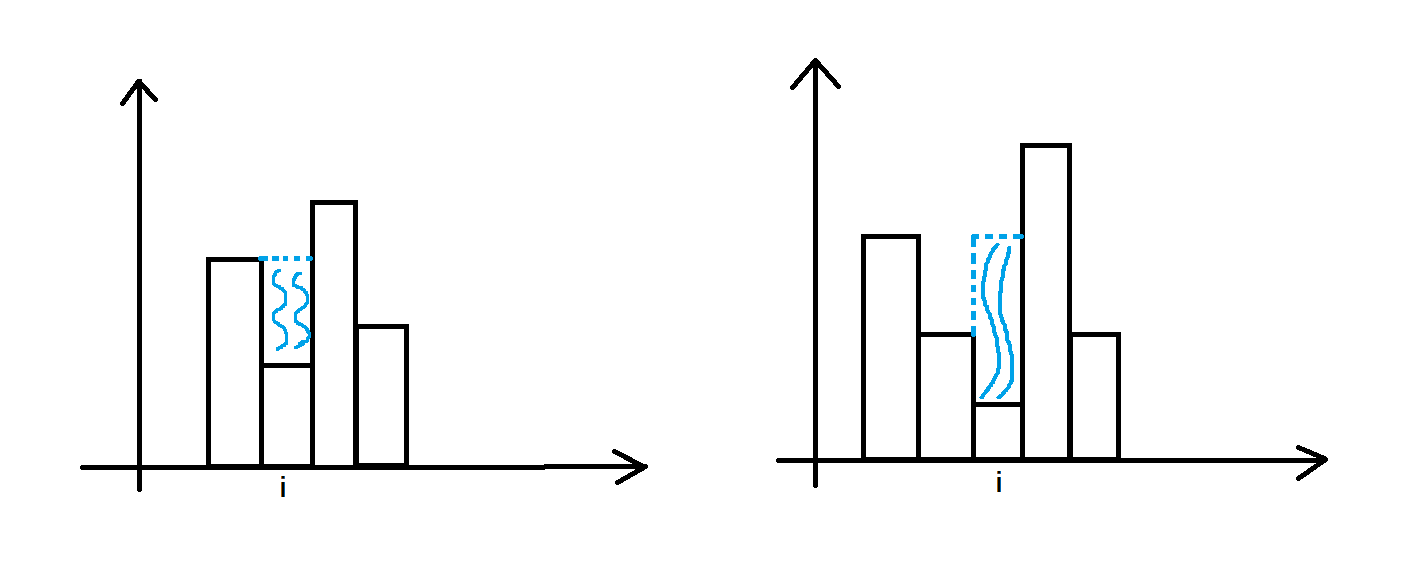
使用双层循环，在遍历每一根柱子的同时，求出第i柱子左右两边高度最高的柱子分别是多少，然后根据两边高度最高柱子中较低的那根柱子去求出第i根柱子最多能接多少雨水。看下图做参考理解

步骤

1. 外层循环遍历每根柱子
   1. 内层嵌套循环①，求第i根柱子左边高度最高的柱子，记录下来max_left
   2. 内层嵌套循环②，求第 i根柱子右边高度最高的柱子，记录下来max_right
   3. max_left与max_right进行比较，算出两边最高的柱子中较低的一根，因为它类似于木桶效应，桶中水的高度总是由较低的木板的高度决定
   4. 如果此时两边柱子中较低的一根柱子比当前遍历的柱子i要高，就说明这根柱子能盛放住雨水
   5. 柱子i能盛放的雨水量就等于它两边最高柱子中较低的一根柱子的高度减去当前柱子的高度，得出结果 将其加入到计算的雨水总量中
2. 返回能接雨水的总量

代码

• 根据代码进一步理解

// 暴力破解，按列求
public int trap(int[] height) {
    int sum = 0;
    int len = height.length;
    for (int i = 1; i < len - 1; i++) {
        int max_left = 0;
        int max_right = 0;
        int min_height = 0;
        //求元素左边最高的柱子
        for (int j = i - 1; j >= 0; j--) {
            if (height[j] > max_left)
                max_left = height[j];
        }

        //求元素右边最高的柱子
        for (int k = i + 1; k < len; k++) {
            if (height[k] > max_right)
                max_right = height[k];
        }
        //求出较低的柱子
        min_height = Math.min(max_left,max_right);
        //比较计算
        if (min_height > height[i])
            sum += min_height - height[i];
    }
    return sum;
}

优化

​ 外层循环是从左到右遍历每根柱子，而内层求左侧最高的柱子的时候又从左到右循环，显然是有冗余的,我们可以使用max_left直接标记左侧最高的柱子，每次只需要比较max_left与前一根柱子的高度大小，而不需要再进行一次遍历

代码如下，改动很小，只将原来求元素左边最高的柱子的for循环改变为if语句

// 暴力破解优化
public int trap(int[] height) {
    int sum = 0;
    int max_left = 0;
    for (int i = 1; i < height.length - 1; i++) {
        //求元素左边最高的柱子
        if (height[i-1] > max_left)
            max_left = height[i-1];

        //求元素右边最高的柱子
        int max_right = 0;
        for (int k = i + 1; k < height.length; k++) {
            if (height[k] > max_right)
                max_right = height[k];
        }
        //求出较低的柱子
        int min_height = Math.min(max_left,max_right);
        //比较计算
        if (min_height > height[i])
            sum += min_height - height[i];
    }
    return sum;
}

参照这个思路，该如何标记遍历时右侧最高的柱子呢？

那么我们就来看下一种解法思路

第二种解法：动态规划求解

思路

我们可以创建两个数组分别记录每根柱子左侧最高的柱子以及右侧最高的柱子

就像我们第一种解法最后的优化思路一样，第i根柱子左侧最高的柱子就等于第i-1根柱子与第i-1根柱子前最高的柱子中较高的一根，也就是max_left[i] = Math.max(max_left[i-1],height[i-1])

那第i根柱子右侧最高的柱子应该怎样算？

我们可以倒序遍历，从右往左遍历柱子，用数组记录下来第i根柱子右侧最高的柱子是那根，类似的，第i+1根柱子与第i+1根柱子右边较高的一根就是第i根 柱子右侧高度最高的柱子，也就是max_right[i] = Math.max(max_right[i+1], height[i+1])

要谨慎对待边界问题

代码

    // 动态规划求解
    public int trap3(int[] height) {
        int sum = 0;
        int[] max_left = new int[height.length];
        int[] max_right = new int[height.length];

        // 每根柱子对应的左边最高的柱子 (注: 并没有使用上一解法的优化做法，而是使用纯种的动态规划，循序渐进，希望可以便于理解)
        for (int i = 1; i < height.length - 1; i++) {
            max_left[i] = Math.max(max_left[i-1],height[i-1]);
        }

        // 每根柱子对应的右边最高的柱子
        for (int i = height.length - 2; i >= 0; i--) {
            max_right[i] = Math.max(max_right[i+1], height[i+1]);
        }

        int min_height = 0;
        for (int i = 1; i < height.length; i++) {
            min_height = Math.min(max_left[i],max_right[i]);
            if (min_height > height[i])
                sum += min_height - height[i];
        }
        return sum;
    }

进行优化的思路

其实，我们在使用数组的过程中 只使用了一个值，这点我们在第一种解法的优化思路中已经说过了，所以说我们只需要各用一个值来记录左右两边的最高柱子就可以，但是循环是从左往右遍历的，所以左侧最高柱子max_left好记录，而右侧我们又想降低空间复杂度，不使用数组来记录最高柱子，那我们应该如何来解决呢？往下看

第三种解法：双指针解决

思路

我们可以使用双指针来很好的解决这个问题，使用left和right分别指向数组两端

我们重新理一下思路，这里不太好想

一根柱子能盛放的水的多少，取决于它左右两边最高的柱子中较低的一根

在遍历的过程中，从左往右遍历我们能知道max_left是确定的，从右往左遍历我们能知道max_right是确定的，而只要我们确定了这两个值中较小的值是多少，我们就可以确定这根柱子能盛多少水，那么另一个较大的值无论多大都不会影响结果。

所以我们可以从两端分别进行遍历，当第left-1根柱子高度小于第right+1根柱子高度时left向右移，我们计算第left根柱子能盛水多少，当第left-1根柱子大于第right+1根柱子高度时right向左移，计算第right根柱子能盛水多少。

我们可以试着这样去理解，从一开始，如果第left-1根柱子高度比第right+1根柱子低，那么max_left就会一直比max_right低，直到通过left指针向右不断移动到了一个使得第left-1根柱子的高度比第right+1根柱子的高度高的情况，那么此时max_left就比max_right更高，我们就可以将right指针向左移。。。这样一次一次通过left-1与right+1的比较以及左右指针的交替使用，我们就可以逐一确定所有柱子能够盛放水的多少

• 双指针的解法非常巧妙，大家请多思考

代码

// 双指针求解
public int trap(int[] height) {
    int sum = 0;
    int max_left = 0;
    int max_right = 0;
    int left = 1;
    int right = height.length - 2;

    for (int i = 1; i < height.length - 1; i++) {
        if (height[left-1] < height[right+1]) {
            max_left = Math.max(max_left,height[left-1]);
            int min = max_left;
            if (min > height[left])
                sum += min - height[left];
            left++;
        }else {
            max_right = Math.max(max_right,height[right+1]);
            int min = max_right;
            if (min > height[right])
                sum += min - height[right];
            right--;
        }
    }

    return sum;
}

第四种解法：单调栈解法

• 除了使用双指针进行优化，我们还可以使用特殊的数据结构来解决

思路

积水存在的原因是什么？

当这根柱子的两侧有比它更高的柱子存在，这根柱子所在的地方就形成了低洼，就能够存储水源

我们从左侧开始遍历，如果一个元素比它的栈顶元素小，就入栈

反之，如果遍历到一个元素，此元素比栈顶元素大，就说明栈顶元素两侧可能形成了高度差，栈顶元素弹出栈，此元素与新的栈顶元素进行判断与计算，直到此元素不大于此时栈顶元素，然后此元素入栈。

代码

// 单调递减栈解法
public int trap1(int[] height) {
    int sum = 0;
    int cur = 0;  //指向的是当前元素
    Deque<Integer> stack = new ArrayDeque<>();
    while (cur < height.length) {
        while (!stack.isEmpty() && height[cur] > height[stack.peek()]) {
            //栈顶元素出栈并赋值给 h
            int h = stack.pop();
            //栈顶元素出栈之后再次判断栈是否为空，如果为空，直接进行下次循环
            if (stack.isEmpty())
                break;
            // 判断当前元素与此时栈顶之间的距离
            int distance = cur - stack.peek() - 1;
            // 求出当前元素与此时栈顶元素中高度较小的一边
            int min_h = Math.min(height[cur],height[stack.peek()]);
            // 求出之前栈顶也就是 h 所能盛放水的多少
            sum += distance * (min_h - height[h]);
        }
        stack.push(cur);
        cur++;
    }
    return sum;
}