Andrew Ng机器学习算法入门(九):逻辑回归

逻辑回归

先前所讲的线性回归主要是一个预测问题，根据已知的数据去预测接下来的情况。线性回归中的房价的例子就很好地说明了这个问题。

然后在现实世界中，很多问题不是预测问题而是一个分类问题。

如邮件是否为垃圾邮件、金融交易是否正常，肿瘤是否是良性的。这新问题都是一个分类。

在分类问题中，结果一般是为0和1，0称为负样本或者是负类，如良性肿瘤。1称为正样本或者是正类，如恶性肿瘤。

那么是否能够使用线性回归的方式来解决分类问题呢？如下是一个辨别肿瘤是良性还是恶性的例子。

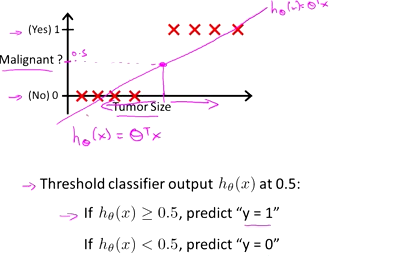
可以看到，貌似线性回归是可以解决分类问题的。

但是如果是下面这个情况，

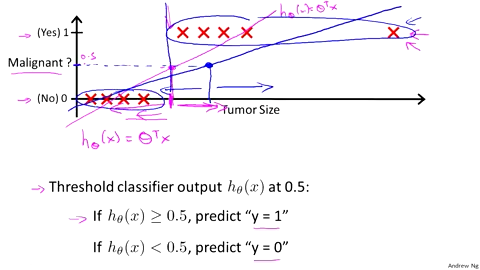
当多了一个数据之后，发现线性回归就存在很明显的偏差。但是这个数据是完全无意义的干扰数据，线性回归为了拟合数据，导致最后的分类出错。在线性回归中还存一个很严重的问题就是，在分类问题中最终的结果只有0和1，但是在线性回归中会出现小于1和大于0的结果。

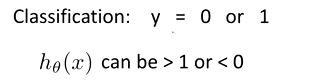
总之，线性回归是不适合处理分类问题的，线性回归问题就可以考虑使用逻辑回归来解决了。

PS:逻辑回归的叫法是历史原因，和回归并没有什么关系。

逻辑回归表示

逻辑回归的表示用下面的一张图来进行说明

其中：

x,表示的是特征向量

g，代表逻辑函数(Logistic function)是一个常用的曲线函数(Sigmoid function),表达式为：

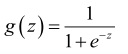
函数的图像就如上图所示。

h,表示的就是逻辑回归，带入到函数g中，最终得到的表达式就是

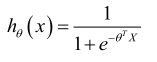
函数h表示的就是当输入特征X时，根据输入的特征计算输出变量Y=1的可能性。假设h(x)=0.7,表示的就是患有恶性肿瘤的概率为0.7

判定边界(Decision Boundary)

判定边界能够让我们更好地理解逻辑回归的函数在进行分类中的意义。

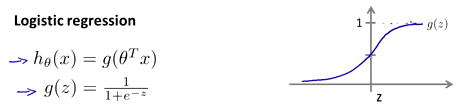
上图就是逻辑回归的函数表示以及图像。

在逻辑回归中，我们预测如果当h>=0.5时，y=1;当h<0.5时，y=0。

当y=1时，要求h>=0.5，意味着g(z)>=0.5,那么就表示z>0,最后就得到了θtX>=0;同理，当y=0时，最后得到θtX<0。

下面就以一个例子来说明问题

其中的theta的参数分别为-3,1,1

存在如上图所示的数据以及表示函数,如果要预测y=1的概率，最后得到的表达式为：

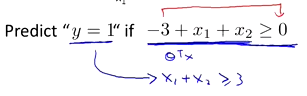
那么最后得到的方程在坐标轴显示的如下：

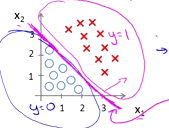
其中的方程就是一个判定边界，通过这条线就可以分辨出正样本和负样本了。

除了这种线性的判定边界之外，还有一些其他形状的判定边界，如圆形。

除了这种线性的判定边界之外，还有一些其他形状的判定边界，如圆形。

逻辑回归中的代价函数

在将逻辑回归中的代价函数之前，先来回顾一下之前讲过的在线性回归中的代价函数。

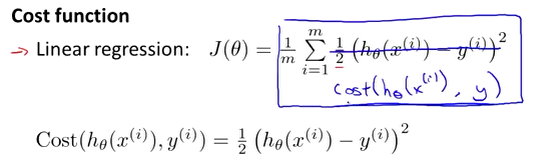
上面就是之前讲过的线性回归中的代价函数，这个代价函数在线性回归中能够很好地使用，但是在逻辑回归中却会出现问题，因为将逻辑回归的表达式带入到h函数中得到的是一个非凸函数的图像，那么就会存在多个局部最优解，无法像凸函数一样得到全局最优解。示例如下。

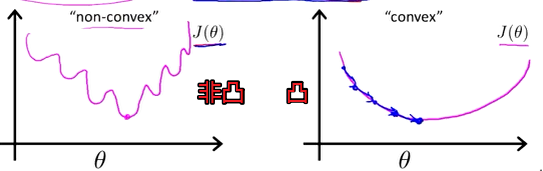
那么在逻辑回归中就需要重新定义代价函数了

逻辑回归中的代价函数为：

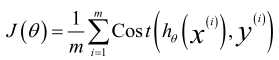
其中

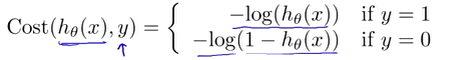
最后得到的函数h和Cost函数之前的关系如下：

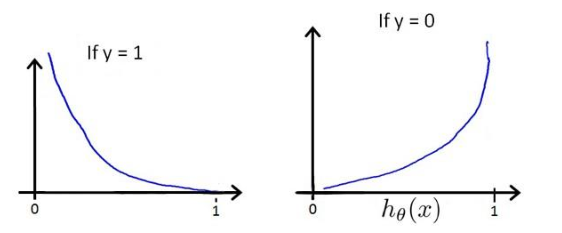
构建一个这样的函数的好处是在于，当y=1时，h=1，如果h不为1时误差随着h的变小而增大；同样，当y=0时，h=0，如果h不为0时误差随着h的变大而增大。

代价函数中的梯度下降

在上一节中的逻辑回归中的代价函数中给出了代价函数的定义，最后可以简化为:

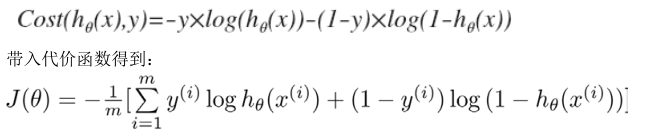
最终的求解问题就是要求回归函数的值最小，那么同样可以使用在线性回归中所用到的梯度函数。

上图就是逻辑回归的梯度求解过程，虽然看起来和线性回归相似，但实则是完全不同的。在线性回归中，h函数为theta的转置与X的乘积，但是在逻辑回归中则不是。这样就导致了两者在运算方面和优化方面是完全不同的。但是在运行梯度下降算法之前，进行特征缩放依旧是非常重要的。

高级优化

优化算法除了讲到的梯度下降算法之外，还有一些叫做共轭梯度下降算法(BFGS,L-BFGS)。使用这些共轭梯度下降算法的好处在于，不需要手动地选择学习率a，这些算法会自行尝试选择a;比梯度下降算法运算更快。

一般情况下，在常见的机器学习算法库中都带有这些算法，不需要程序员手动实现这些算法。

多类别分类问题

现实世界中除了二元的分类问题还有多元的分类问题，如对天气的分类，是晴天、多云、小雨等等天气。

多元分类问题与二元分类问题的区别如下:

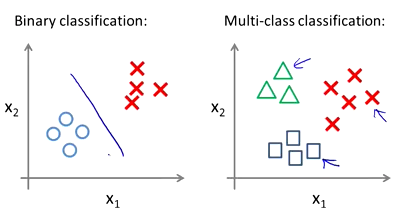
多元分类的思路与二元分类问题的解决思路是类似的。可以将多元问题变为两元问题，具体如下：

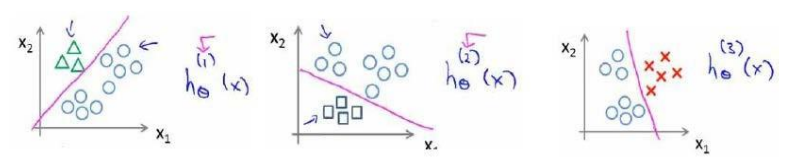
这样n元的分类问题，就会进行n次的机器学习的分类算法。对每一次的分类结果即为h(x)。那么经过n此分类之后，最后得到的结果为:

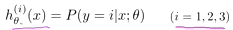
那么当输入新的训练集或者是变量X，只需要按照上面的思路进行分类，其中的h(x)的最大值就是对应的最后的分类结果。

为了能到远方，脚下的每一步都不能少