矩阵旋转-Eigen应用（QTCreator编辑器）

* { font-family: "Tibetan Machine Uni", "sans-serif", STFangSong; outline: none }

一、概述

1. 旋转变换的核心思想

   在不同坐标系下，虽然坐标不同，但是同一个向量还是一样的。这句话有点儿怪怪的，但是可以用数学公式表出：\(\beta_1^T\cdot\alpha_1=\beta_2^T\cdot\alpha_2\)，其中\(\beta\)是不同坐标系的标准正交基（行分块），\(\alpha\)是不同坐标系下的坐标（列向量）。

2. 旋转变换的五种表述

   1. 旋转矩阵；
   2. 欧式矩阵；
   3. 旋转向量；
   4. 欧拉角；
   5. 四元数；

3. 旋转变换表述的演替

   1. 旋转矩阵和平移矩阵：有小尾巴累积（非线性）
   2. 欧式矩阵：n+1维方阵要\((n+1)^2\)个自由度，太多了（线性，但不紧凑且不直观）
   3. 旋转向量：这是什么呀这一堆数？！看不懂！（紧凑但不直观）
   4. 欧拉角：这会看懂了…等等，这转个90\(^\circ\)咋就膈屁了呢？！（紧凑直观但奇异）
   5. 四元数：爱咋转咋转…等等不对！咋1个\(R\)冒俩\(q\)呢？\(q\)咋还内讧了呢？（紧凑非奇异，但不唯一且不稳定）

4. 在Eigen库中它们四个大哥（欧式矩阵对不起，现在我们只考虑旋转）的转换关系

   旋转向量和四元数先初始化（默认定义为‘单位阵’，不能赋值为nullptr或者直接使用）！！！

   1. 旋转矩阵

      1. 初始化旋转矩阵

         Eigen::Matrix3d rotation_matrix;
         // 通过标准输入设备（标准输入流）键入赋值
         rotation_matrix << x_00,x_01,x_02,x_10,x_11,x_12,x_20,x_21,x_22;
         

      2. 旋转矩阵 \(\Longrightarrow\) 旋转向量

         // 第一种：通过构造函数（传入一个旋转矩阵）
         Eigen::AngleAxisd rotation_vector(rotation_matrix);
         // 第二种：首先初始化，然后通过旋转矩阵直接赋值（重载了赋值运算符）
         Eigen::AngleAxisd rotation_vector;
         rotation_vector = rotation_matrix;
         // 第三种：首先初始化，然后from函数直接作用于this对象（rotation_vector）
         Eigen::AngleAxisd rotation_vector;
         rotation_vector.fromRotationMatrix(rotation_matrix);
         

      3. 旋转矩阵 \(\Longrightarrow\) 欧拉角

         // (2, 1, 0)表示旋转顺序ZYX，数字越小表示优先级越高
         Eigen::Vector3d euler_angle = rotation_matrix.eulerAngles(2, 1, 0);
         

      4. 旋转矩阵 \(\Longrightarrow\) 四元数

         // 第一种：通过构造函数（传入一个旋转矩阵）
         Eigen::Quaterniond quaternion(rotation_matrix);
         // 第二种：首先初始化，然后通过旋转矩阵直接赋值（重载了赋值运算符）
         Eigen::Quaterniond quaternion;
         quaternion = rotation_matrix;
         

   2. 旋转向量

      1. 初始化旋转向量

         // 通过构造函数
         Eigen::AngleAxisd rotation_vector(alpha, Vector3d(x,y,z));
         

      2. 旋转向量 \(\Longrightarrow\) 旋转矩阵

         // 第一种方法：通过构造方法传入旋转向量
         Eigen::Matrix3d rotation_matrix(rotation_vector);
         // 第二种方法：首先初始化，然后通过旋转向量直接赋值（重载了赋值运算符）
         Eigen::Matrix3d rotation_matrix;
         rotation_matrix = rotation_vector;
         // 第三种方法：通过matrix方法
         Eigen::Matrix3d rotation_matrix = rotation_vector.matrix();
         // 第四种方法：通过toRotationMatrix方法
         Eigen::Matrix3d rotation_matrix = rotation_vector.toRotationMatrix();
         

      3. 旋转向量 \(\Longrightarrow\) 欧拉角

         // 不能直接转换，需要通过旋转矩阵搭桥
         Eigen::Vector3d euler_angles = rotation_vector.matrix().eulerAngles(2, 1, 0);
         

      4. 旋转向量 \(\Longrightarrow\) 四元数

         // 第一种方法：通过构造函数传入旋转向量
         Eigen::Quaterniond quaterniond(rotation_vector);
         // 第二种方法：首先初始化，然后用旋转向量赋值
         Eigen::Quaterniond quaterniond;
         quaterniond = rotation_vector;
         

   3. 欧拉角

      1. 初始化欧拉角

         Eigen::Vector3d euler_angles(yaw, pitch, roll);
         

      2. 欧拉角 \(\Longrightarrow\) 旋转矩阵

         // 初始化三个旋转角的旋转向量
         Eigen::AngleAxisd rollAngle(AngleAxisd(euler_angles(2),Eigen::Vector3d::UnitX()));
         Eigen::AngleAxisd pitchAngle(AngleAxisd(euler_angles(1),Eigen::Vector3d::UnitY()));
         Eigen::AngleAxisd yawAngle(AngleAxisd(euler_angles(0),Eigen::Vector3d::UnitZ()));
         // 先初始化旋转矩阵为单位矩阵，然后这三个旋转向量相乘得到旋转矩阵（运算符重载）
         Eigen::Matrix3d rotation_matrix;
         rotation_matrix = yawAngle * pitchAngle * rollAngle;
         

      3. 欧拉角 \(\Longrightarrow\) 旋转向量

         // 初始化三个旋转角的旋转向量
         Eigen::AngleAxisd rollAngle(AngleAxisd(euler_angles(0), Eigen::Vector3d::UnitX()));
         Eigen::AngleAxisd pitchAngle(AngleAxisd(euler_angles(1), Eigen::Vector3d::UnitY()));
         Eigen::AngleAxisd yawAngle(AngleAxisd(euler_angles(2), Eigen::Vector3d::UnitZ()));
         // 先初始化旋转向量，然后这三个旋转向量相乘得到旋转向量（运算符重载）
         Eigen::AngleAxisd rotation_vector;
         rotation_vector = yawAngle * pitchAngle * rollAngle;
         

      4. 欧拉角 \(\Longrightarrow\) 四元数

         // 初始化三个旋转角的旋转向量
         Eigen::AngleAxisd rollAngle(AngleAxisd(euler_angles(2),Eigen::Vector3d::UnitX()));
         Eigen::AngleAxisd pitchAngle(AngleAxisd(euler_angles(1),Eigen::Vector3d::UnitY()));
         Eigen::AngleAxisd yawAngle(AngleAxisd(euler_angles(0),Eigen::Vector3d::UnitZ()));
         // 先初始化四元数，然后这三个旋转向量相乘得到旋转向量（运算符重载）
         Eigen::Quaterniond quaterniond;
         quaterniond = yawAngle * pitchAngle * rollAngle;
         

   4. 四元数

      1. 初始化四元数

         Eigen::Quaterniond quaterniond(w, x, y, z);
         

      2. 四元数 \(\Longrightarrow\) 旋转矩阵

         // 第一种方法：通过构造方法传入四元数
         Eigen::Matrix3d rotation_matrix(quaterniond);
         // 第二种方法：首先初始化，然后通过四元数直接赋值（重载了赋值运算符）
         Eigen::Matrix3d rotation_matrix;
         rotation_matrix = quaterniond;
         // 第三种方法：通过matrix方法
         Eigen::Matrix3d rotation_matrix = quaterniond.matrix();
         // 第四种方法：通过toRotationMatrix方法
         Eigen::Matrix3d rotation_matrix = quaterniond.toRotationMatrix();
         

      3. 四元数 \(\Longrightarrow\) 旋转向量

         // 第一种方法：通过构造函数传入一个四元数
         Eigen::AngleAxisd rotation_vector(quaterniond);
         // 第二种方法：通过四元数直接赋值（运算符重载）
         Eigen::AngleAxisd rotation_vector;
         rotation_vector = quaterniond;
         

      4. 四元数 \(\Longrightarrow\) 欧拉角

         // 不能直接转换，需要靠旋转矩阵搭桥
         Eigen::Vector3d euler_angles = quaterniond.matrix().eulerAngles(2, 1, 0);
         

   5. 在Eigen中的转换——总结篇

      

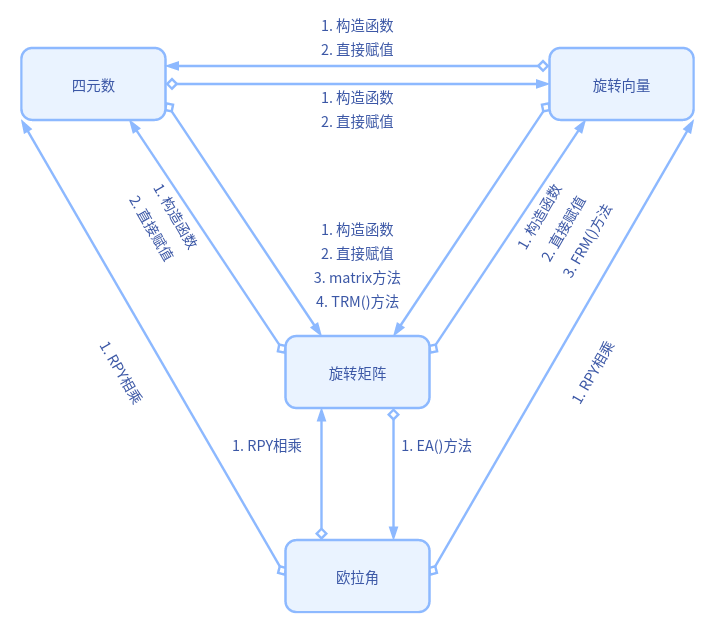
      1. 旋转矩阵到旋转向量的FRM()方法是fromRotationMatrix()；
      2. 四元数和旋转向量到旋转矩阵用的同一套体系，其中TRM()方法是toRotationMatrix()；
      3. 只有旋转矩阵才能直接转换为欧拉角，其EA()方法为eulerAngles()；
      4. 欧拉角转换成其他旋转表述形式用的同一套体系：RPY相乘。先初始化三个旋转角（RPY）的旋转向量，然后初始化所需旋转表述形式，最后这三个旋转向量相乘得到相应旋转表述形式（运算符重载）；

5. 旋转表述的使用

   1. 旋转矩阵

      Eigen::Vector3d v( 1,0,0 );
      v_rotated = rotation_matrix * v;
      

   2. 欧式矩阵

      Eigen::Vector3d v( 1,0,0 );
      Eigen::Isometry3d T=Eigen::Isometry3d::Identity();
      // 为欧式矩阵设置旋转矩阵
      T.rotate(rotation_vector);
      // 为欧式矩阵设置平移矩阵
      T.pretranslate(Eigen::Vector3d(1, 3, 4));
      Eigen::Vector3d v_transformed = T * v;
      

   3. 旋转向量

      Eigen::Vector3d v( 1,0,0 );
      Eigen::Vector3d v_rotated = rotation_vector * v;
      

   4. 欧拉角

      Eigen::Vector3d v( 1,0,0 );
      Eigen::Vector3d euler_angles(M_PI / 4, M_PI / 4, M_PI / 4);
      // 通过上述转换：rotation_matrix !!!
      Eigen::Vector3d v_rotated = rotation_matrix * v;
      

   5. 四元数

      Eigen::Vector3d v( 1,0,0 );
      Eigen::Quaterniond q = Eigen::Quaterniond(rotation_vector);
      // 注意数学上的表达式是：qvq^{-1}
      Eigen::Vector3d v_rotated = q * v;
      

二、详述

1. 旋转矩阵

   1. 旋转矩阵的定义

      \[\begin{aligned}
      &由旋转的本质方程：\beta_1^T\alpha_1=\beta_2^T\alpha_2，
      又由于\beta是标准正交基，所以\beta\beta^T = E；
      \\
      &所以两边同时乘上\beta_1，故而可得\alpha_1=\beta_1\beta_2^T\alpha_2，记旋转矩阵R=\beta_1\beta_2^T；
      \end{aligned}
      \]

   2. 旋转矩阵各个参数的意义

      \(\beta\)是标准正交基，\(\alpha\)是相应坐标系下的坐标。

   3. 旋转矩阵各个参数的计算

      \(R=\beta_1\beta_2^T\)。

2. 欧式矩阵

   1. 欧式矩阵的定义

      \[T =
      \left[
      \begin{matrix}
      R&t\\
      \it{0}^T&1
      \end{matrix}
      \right]
      \]

   2. 欧式矩阵各个参数的意义

      \(R\)是旋转矩阵，\(t\)是平移向量，\(\it{0}^T\)是0列向量。

   3. 欧式矩阵各个参数的计算

      不用计算，直接就有！！！

3. 旋转向量

   1. 旋转向量的定义

      \[\overrightarrow{n}与旋角\theta
      \]

   2. 旋转向量各个参数的意义

      任何一个向量（或称为点）^【1】的旋转都是绕着一个特定的轴来旋转，我们可以用这个轴的长度保存旋转角的大小\(\theta\)。故而旋转角被定义为：\(\theta\overrightarrow{n}\)。

      【注】^【1】：这里本来是坐标系的旋转，但是我们用相对的眼光看问题，我们如果聚焦于坐标系的话就相当与是向量在旋转。一个向量绕着一个轴在转可能比坐标系绕着一个轴在转好理解一点，这俩本质一样。

   3. 旋转向量各个参数的计算

      1. 旋转轴\(\overrightarrow{n}\)的计算

         旋转轴在旋转的时候是不会变化的，所以有：\(R\overrightarrow{n}=\overrightarrow{n}\)，即有\(\overrightarrow{n}\)为\(R\)的特征值为1的特征向量。

      2. 旋转角\(\theta\)的计算

         罗德格里斯指出了旋转向量到旋转矩阵的法则：\(R=\cos{\theta}I+(1-\cos{\theta})\overrightarrow{n}\overrightarrow{n}^T+\sin{\theta}\overrightarrow{n}^{\wedge}\)。

         同时取迹可得：\(\mathbf{tr}(R)=1+2\cos{\theta}\)。所以就计算出了\(\theta=\arccos{\frac{\mathbf{tr}(R)-1}{2}}\)。

4. 欧拉角

   1. 欧拉角的定义

      每个轴旋转一个特定的角度，但是有顺序要求，我们一般使用ZYX的顺序（称为RPY）。

   2. 欧拉角各个参数的意义

      1. R：Roll，偏航角

      2. P：Pitch，翻滚角

      3. Y：Yaw，俯仰角

   3. 欧拉角各个参数的计算

      通过传感器或者人为给出。不是吧不是吧，不会真有人用欧拉角吧？！^【1】

      【注】^【1】：万向锁问题（奇异性）问题——只要我们想用3个实数来表达3维旋转时，都会不可避免地碰到奇异性问题。所以很少用这样的旋转表述方式，一般用也只是用于人机交互中传入旋转角度，或者验证系统的算法，因为这样的表述对于人类来说是非常直观的。

5. 四元数

   1. 四元数的定义

      \[q=(s，\overrightarrow{v})^{T}=(s，x，y，z)^{T}=s+xi+yj+zk
      \]

   2. 四元数各个参数的意义

      1. 实部\(s\)表示旋转程度：\(s=f(\theta)\)；

      2. 虚部\(\overrightarrow{v}\)表示旋转轴：\(\overrightarrow{v}=k\overrightarrow{n}\)；

         虚部\(\overrightarrow{v}\)的定义为某个点在三维直角系下的坐标，由于四元数表示对一个向量（或称为点）的旋转，用数学公式可以严谨地证明，当对\(\overrightarrow{v}\)进行\(q=(s，\overrightarrow{v})^{T}\)旋转时不变，所以\(\overrightarrow{v}\)表示旋转轴。

   3. 四元数各个参数的计算（利用旋转向量）

      1. 实部\(s\)的计算

         1. 四元数 \(\Longrightarrow\) 旋转矩阵

            \[\begin{aligned}
            R& = \overrightarrow{v}\overrightarrow{v}^{T}+s^2I+2s\overrightarrow{v}^{\wedge}+(\overrightarrow{v})^2
            \\\\
            \mathbf{tr}(R)&=4s^2-1
            \end{aligned}
            \]

         2. 旋转矩阵 \(\Longrightarrow\) 旋转向量

            \[\begin{aligned}
            \theta& = \arccos(\frac{\mathbf{tr}(R)-1}{2})=\arccos(2s^2-1)
            \\\\
            \theta& = 2\arccos{s}
            \\\\
            s& = \cos{\frac{\theta}{2}}
            \end{aligned}
            \]

      2. 虚部\(\overrightarrow{v}\)的计算

         1. 得到旋转轴

            旋转轴就是四元数的虚部\(\overrightarrow{v}\)。

         2. 将四元数单位化

            我们已经知道了实部\(s=\cos{\frac{\theta}{2}}\)，所以虚部向量就只用除以一个\(\sin{\frac{\theta}{2}}\)就行了。