BQ40Z50固件怎么升级？告诉你BQ系列芯片内部结构和升级方法

一 BQ芯片初步认识

包括BQ40Z50在内，BQ系列电池管理芯片看起来是一个芯片，其实芯片里面封装了两个die。一个是MCU部分负责计算和控制，其采用的是bqBMP内核的16位处理器；另外一个die是模拟前端AFE，负责模拟信号处理部分，主要功能是处理电压电流温度信号，包括放大，MUX，MOS驱动和一些硬件保护逻辑。两个芯片的绑定类似下图结构：

二 BQ芯片内部结构

MCU和AFE间主要接口有：电流采样库仑计CC，电压温度采样ADC，GPIO和专用串口通信。类似我们用分立器件MSP430+BQ76925的架构。

主要结构见下图所示：

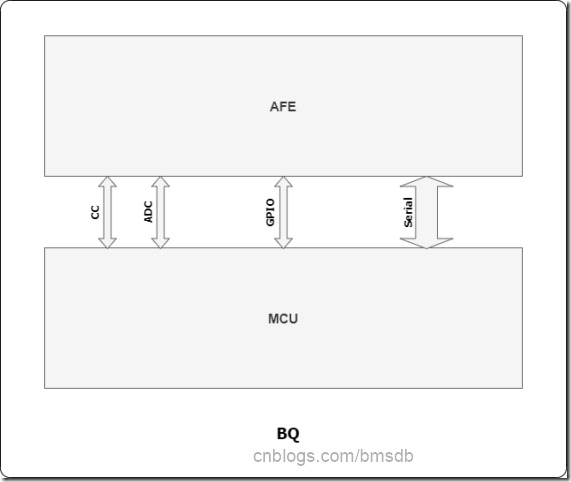
MCU和AFE封装在一起是不得已而为之，也具有明显的优势：

• MCU主要负责计算和控制逻辑，是低压部分，而AFE主要负责高压部分处理，两个芯片工艺不同，在一个die上实现比较困难；

• 封装在一起，对外呈现的是一个芯片，使用方便，真正做到低耦合高内聚；

• 封装后固件也是由TI提供，稳定性比较好保证；

• 封装也利于电量计算法的实现，提高芯片价值。举例，BQ40Z50比BQ4050就贵不少。

对于BQ40Z50芯片，芯片架构细节如图所示：

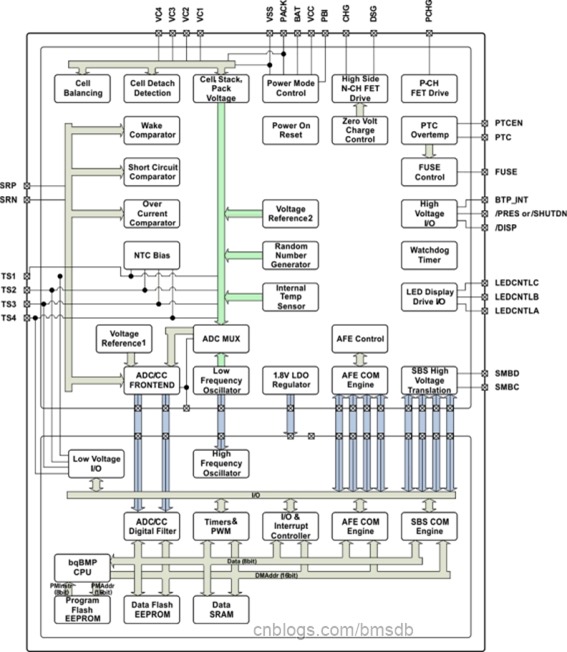
TI专用内核bqBMP处理器是哈弗结构，数据总线和程序总线独立，其基本特征有：

CPU是16位的
运行速度4.2MHz
三级流水线
指令长度灵活，可以支持8位、16位、24位指令

三 BQ40Z50内部存储器结构

内部存储器包括Flash，Boot ROM Flash， RAM，Data Flash和EEPROM。其中Flash一共有64K大小，RAM 2.5K, Data Flash 8K, EEPROM 0.5K.

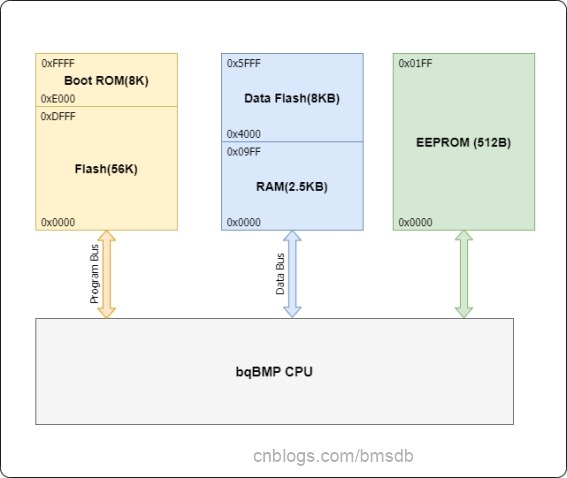
Boot ROM是芯片的Bootloader，承担启动加载和固件升级作用，芯片固化好，不可修改和升级。

我们通过BQ Studio读出来的SREC文件，包括Data Flash， Program Flash和EEPROM的数据，也是除了Bootloader外的所有数据。

注意：

TI的电池管理芯片内的CPU core有两代，BQ30Z55 BQ3055 BQ34Z100 BQ27541 BQ27542 BQ78350是比较老的一代，已经逐步淘汰；
BQ40Z50同平台的有BQ40Z80，BQ78Z100，BQ27Z561等，推荐使用这一个系列。

四固件升级方案

通过以上对CPU架构和存储结构的了解，我们对实现电量计芯片升级有个思路了。它跟普通MCU升级有相似的地方，只是要对芯片充分了解，可以做到不用bqStudio也能升级固件。

实际工作中，我们可能遇到以下问题：

1 已经校准的电池需要返工，通过bqStudio升级固件会擦除掉校准值和电量计学习的数据

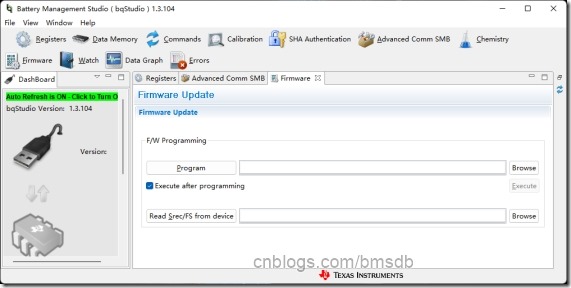
解决方法：我们就可以不用bqStudio，专门编个PC软件，控制EV2400/EV2300，跳过升级data flash部分，只升级Program flash；

2 发现固件Bug，但由于固件已经发布，或者电池是串口的等原因，不能用电脑软件升级。

解决方法：主控来实现升级策略，可以升级电池的固件和配置参数，这个方法我们在无人机上已经实现。

3 已经发给客户的电池需要升级，并且数量很大，用PC软件效率太低。

解决方法：针对这种情况，也可以专门做个小板，内部存储电量计固件，连上电池就自动升级。

这个可以50个100个同时工作，也很快能完成电池升级的问题。

事实上，我们也的确遇见这个问题，就做了个带SD卡的小板，将固件放到SD卡里面，一连接电池就会执行自动升级。

以上都是作者多年与BQ电量计打交道，通过研究或与原厂共同开发得到的经验，希望能对做电池的你有所帮助。

博客内都是原创文章，转载请注明出处。