【做题记录】[NOIP2016 普及组] 魔法阵

P2119 魔法阵

2016年普及组T4

题意：

给定一系列元素 \(\{X_i\}\) ，求满足以下不等式的每一个元素作为 \(a,b,c,d\) 的出现次数 。

\[\begin{cases}X_a<X_b<X_c<X_d \\ X_a-X_b=2\times (X_d-X_c) \\X_b-X_a<\dfrac{X_c-X_b}{3}\end{cases}
\]

题解：

设 \(X_d-X_c=t\) ，则 \(X_a-X_b=2\times t\) 。

带入第三个式子，可得：\(2\times t<\dfrac{X_c-X_b}{3}\) 。

变形得：\(6\times t+k=X_c-X_b\) ，其中 \(1\le k\le n\) 。

因为 \(A\ge 1\) 且 \(D\le n\) ，所以 \(1\le9\times t \le n-1\) 。

则有了这么一幅图：

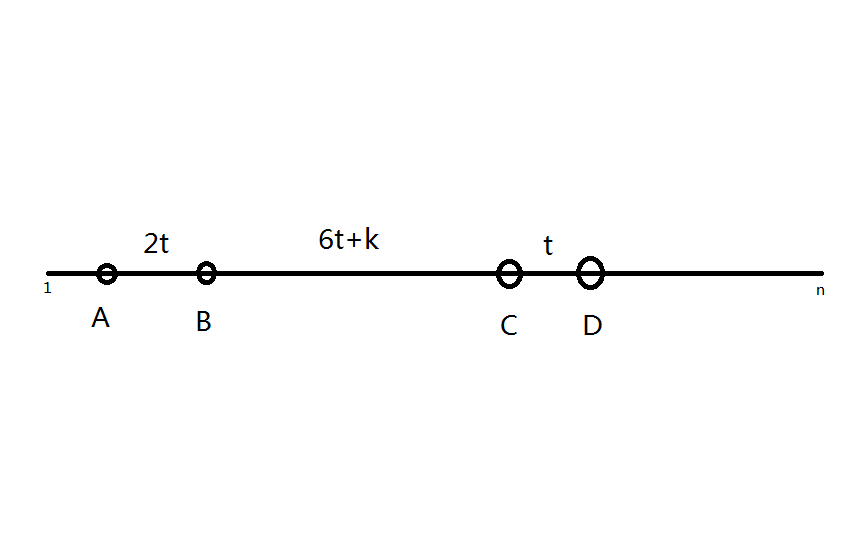
考虑枚举 \(t\) ：

• 枚举 \(A=[n-9\times t-1,\dots,1]\) ：

  对于一对 \([A,B]\) ，\([C,D]\) 的最小值当 \(k=1\) 时取到 。而对于一对能形成魔法阵的 \([X_c,X_d]\) ，\([X_i(X_i>=X_c),X_j(X_j>X_d)]\) ,也能形成魔法阵 。则可以用后缀和优化 。

• 枚举 \(D=[2+9\times t,\dots,n]\) ：同理，用前缀和优化 。

代码：

int n,m,a[Maxn],cnt[Maxn],ans[4][Maxn];

n=rd(),m=rd();
for(int i=1;i<=m;i++) a[i]=rd(),cnt[a[i]]++;
for(int t=1,tmp;9*t<n;t++)
{
	 tmp=0; for(int A=n-t*9-1;A>=1;A--)
	 {
	 	 int D=A+t*9+1,B=A+2*t,C=D-t;
	 	 tmp+=cnt[C]*cnt[D];
	 	 ans[0][A]+=tmp*cnt[B];
	 	 ans[1][B]+=tmp*cnt[A];
	 }
	 tmp=0; for(int D=t*9+2;D<=n;D++)
	 {
	 	 int A=D-t*9-1,B=A+t*2,C=D-t;
	 	 tmp+=cnt[A]*cnt[B];
	 	 ans[2][C]+=tmp*cnt[D];
	 	 ans[3][D]+=tmp*cnt[C];
	 }
}
for(int i=1;i<=m;i++) printf("%d %d %d %d\n",ans[0][a[i]],ans[1][a[i]],ans[2][a[i]],ans[3][a[i]]);