统计学习：线性支持向量机(SVM)

学习策略

软间隔最大化

上一章我们所定义的“线性可分支持向量机”要求训练数据是线性可分的。然而在实际中，训练数据往往包括异常值(outlier)，故而常是线性不可分的。这就要求我们要对上一章的算法做出一定的修改，即放宽条件，将原始的硬间隔最大化转换为软间隔最大化。

给定训练集

\[\begin{aligned}
D = \{\{\bm{x}^{(1)}, y^{(1)}\}, \{\bm{x}^{(2)}, y^{(2)}\},..., \{\bm{x}^{(m)}, y^{(m)}\}\}
\end{aligned}\tag{1}
\]

其中\(\bm{x}^{(i)} \in \mathcal{X} \subseteq \mathbb{R}^n\)，\(y^{(i)} \in \mathcal{Y} = \{+1, -1\}\)。

如果训练集是线性可分的，则线性可分支持向量机等价于求解以下凸优化问题：

\[\begin{aligned}
\underset{\bm{w}, b}{\max} \quad \frac{1}{2} || \bm{w}||^2\\
\text{s.t.} \quad y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b) \geqslant 1 \\
\quad (i = 1, 2, ..., m)
\end{aligned} \tag{2}
\]

其中\(y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b) -1 \geq 0\)表示样本点\((\bm{x}^{(i)}, y^{(i)})\)满足函数间隔大于等于1。现在我们对每个样本点\((\bm{x}^{(i)}, y^{(i)})\)放宽条件，引入一个松弛变量\(\xi_{i} \geqslant 0\),使约束条件变为\(y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b) \geq 1-\xi_{i}\)。并对每个松弛变量进行一个大小为\(\xi_{i}\)的代价惩罚，目标函数转变为：\(\frac{1}{2} || \bm{w}||^2+C\sum_{i=1}^{m}\xi_{i}\)，此处\(C>0\)称为惩罚系数。此时优化函数即要使间隔尽量大（使\(\frac{1}{2} || \bm{w}||^2\)尽量小）,又要使误分类点个数尽量少。这称之为软间隔化。

线性支持向量机

就这样，线性支持向量机变为如下凸二次规划问题(原始问题)：

\[\begin{aligned}
\underset{\bm{w}, b}{\max} \quad \frac{1}{2} || \bm{w}||^2 + C\sum_{i=1}^{m}\xi_{i}\\
\text{s.t.} \quad y^{(i)} (\bm{w}^T \bm{x}^{(i)} + b) \geqslant 1-\xi_{i} \\
\xi_{i} \geqslant 0 \\
\quad (i = 1, 2, ..., m)
\end{aligned} \tag{3}
\]

因为是凸二次规划，因此关于\((\bm{w}, b, \bm{\xi})\)的解一定存在，可以证明\(\bm{w}\)的解唯一，但\(b\)的解可能不唯一，而是存在于一个区间。

设\((2)\)的解为\(\bm{w}^{*}, b^*\)，这样可得到分离超平面\(\{\bm{x} | \bm{w}^{*T}\bm{x}+b=0\}\)和分类决策函数\(f(\bm{x})=\text{sign}(\bm{w}^{*T}\bm{x}+b^*)\)

算法

常规的带约束优化算法

和上一章一样，我们将原始问题\((2)\)转换为对偶问题进行求解，原始问题的对偶问题如下（推导和上一章一样）：

\[\begin{aligned}
\underset{\bm{\alpha}}{\max} -\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy^{(i)}y^{(j)}\langle \bm{x}^{(i)}, \bm{x}^{(j)}\rangle + \sum_{i=1}^{m}\alpha_i \\
s.t. \sum_{i=1}^{m}\alpha_iy^{(i)} = 0 \\
C - \alpha_i - \mu_i = 0\\
\alpha_i \geq 0 \\
\mu_i \geq 0 \\
i=1, 2,...,m
\end{aligned}
\tag{4}
\]

接下来我们消去\(\mu_i\)，只留下\(\alpha_i\)，将约束条件转换为：\(0 \leqslant \alpha_i \leqslant C\) ，并对目标函数求极大转换为求极小，这样对\((4)\)进行进一步变换得到：

\[\begin{aligned}
\underset{\bm{\alpha}}{\max} -\frac{1}{2}\sum_{i=1}^{m}\sum_{j=1}^{m}\alpha_i\alpha_jy^{(i)}y^{(j)}\langle \bm{x}^{(i)}, \bm{x}^{(j)}\rangle + \sum_{i=1}^{m}\alpha_i \\
s.t. \sum_{i=1}^{m}\alpha_iy^{(i)} = 0 \\
0 \leqslant \alpha_i \leqslant C \\
i=1, 2,...,m
\end{aligned}
\tag{5}
\]

这就是原始优化问题\((3)\)的对偶形式。



这样，我们得到对偶问题的解为\(\bm{\alpha}^*=(\alpha_1^*, \alpha_2^*, ..., \alpha_m^*)^T\)。

此时情况要比完全线性可分时要复杂，比如正例不再仅仅分布于软间隔平面上和正例那一侧，还可能分布于负例对应的那一侧（由于误分）；对于负例亦然。如下图所示：

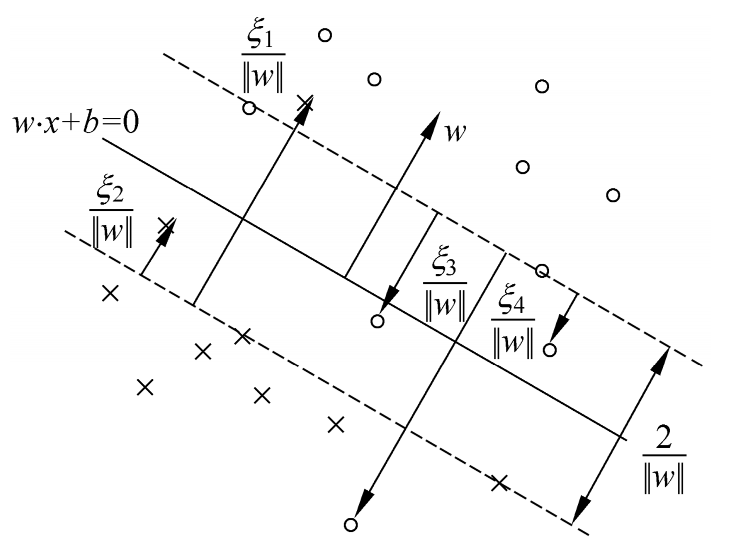
图中实线为超平面，虚线为间隔边界，“\(\circ\)”为正例点，“\(\times\)”为负例点，\(\frac{\xi_i}{||\bm{w}||}\)为实例\(\bm{x}^{(i)}\)到间隔边界的距离。

此时类比上一章，我们将\(\alpha_i^* > 0\)（注意，不要求一定有\(\alpha_i^*<C\)）对应样本点\((\bm{x}^{(i)}, y^{(i)})\)的实例\(\bm{x}^{(i)}\)称为支持向量（软间隔支持向量）。它的分布比硬间隔情况下要复杂得多：可以在间隔边界上，也可以在间隔边界和分离超平面之间，甚至可以在间隔超平面误分类的一侧。若\(0<\alpha_i^*<C\)，则\(\xi_i =0\)，支持向量恰好落在间隔边界上；若\(\alpha_i = C, 0<\xi_i<1\)，则分类正确且\(\bm{x}^{(i)}\)在间隔边界和分离超平面之间；若\(\alpha_i^*=C, \xi_i=1\)，则\(\bm{x}^i\)在分离超平面上；若\(\alpha_i^*=C, \xi_i>1\)则分类错误，\(\bm{x}^{(i)}\)分离超平面误分类的那一侧。

接下来我们需要将对偶问题的解转换为原始问题的解。



对于对偶问题的解\(\bm{\alpha}^*=(\alpha_1^*, \alpha_2^*, ..., \alpha_m^*)^T\),若存在\(\alpha^*\)的一个分量\(0 <\alpha_s^* < C\)，则原始问题的解\(w^*\)和\(b^*\)可以按下式求得：

\[\begin{aligned}
\bm{w}^{*} = \sum_{i=1}^{m}\alpha_i^{*}y^{(i)}\bm{x}^{(i)} \\
b^{*} = y^{(s)} - \sum_{i=1}^{m}\alpha_i^*y^{(i)}\langle \bm{x}^{(s)}, \bm{x}^{(i)} \rangle
\end{aligned}
\tag{6}
\]

式 \((11)\) 的推导方法和上一章类似，由原始问题(凸二次规划问题)的解满足KKT条件导出。





这样，我们就可以得到分离超平面如下：

\[\{\bm{x} | \sum_{i=1}^{m}\alpha_i^*y^{(i)}\langle \bm{x}^{(i)}, \bm{x} \rangle + b^* = 0\}
\tag{7}
\]

分类决策函数如下:

\[f(\bm{x}) = \text{sign}(\sum_{i=1}^{m}\alpha_i^*y^{(i)}\langle \bm{x}^{(i)}, \bm{x} \rangle + b^*)
\tag{8}
\]

(同样地，之所以写成\(\langle \bm{x}^{(i)}, \bm{x} \rangle\)的内积形式是为了方便我们后面引入核函数)



综上，按照式\((3)\)的策略求解线性可分支持向量机的算法如下：　



可以看到在算法的步骤\((2)\)中，是对随机采的一个\(\alpha_s^*\)计算出\(b^*\)，故按照式\((3)\)的策略（原始问题）求解出的\(b\)可能不唯一。

基于合页损失函数的的无约束优化算法

其实，问题\((3)\)还可以写成无约束优化的形式，目标函数如下：

\[ \underset{\bm{w}, b}{\min} \space \frac{1}{m}\sum_{i=1}^{m}\max(0, 1-y^{(i)}(\bm{w}^{T}\bm{x}^{(i)} + b))+\lambda||\bm{w}||^2
\tag{9}
\]

式\((8)\)的第一项为经验风险或经验损失（加上正则项整体作为结构风险）。函数

\[ L(y(\bm{w}^{T}\bm{x} + b))=\max(0, 1-y(\bm{w}^{T}\bm{x} + b))
\tag{10}
\]

称为合页损失函数（hinge loss function）。s

合页损失函数意味着：如果样本\((\bm{x}^{(i)}, y^{(i)})\)被正确分类且函数间隔（确信度）大于1（即\(y^{(i)}(\bm{w}^{T}\bm{x}^{(i)} + b)>0\)），则损失是0，否则损失是\(1-y^{(i)}(\bm{w}^{T}\bm{x}^{(i)} + b)\)。像上面提到的分类图中，\(\bm{x}^{(4)}\)被正确分类，但函数间隔不大于1，损失不是0。

0-1损失函数、合页损失函数、感知机损失函数归纳如下：

\[ \begin{aligned}
0-1损失函数:\quad \quad \text{I}(y(\bm{w}^{T}\bm{x}+b)<0) \\
合页损失函数:\quad \quad\max(0, 1-y(\bm{w}^{T}\bm{x} + b)) \\
感知机损失函数:\quad \quad\max(0, -y(\bm{w}^{T}\bm{x} + b))
\end{aligned}
\tag{11}
\]

这三个函数的图像对比如下图所示：

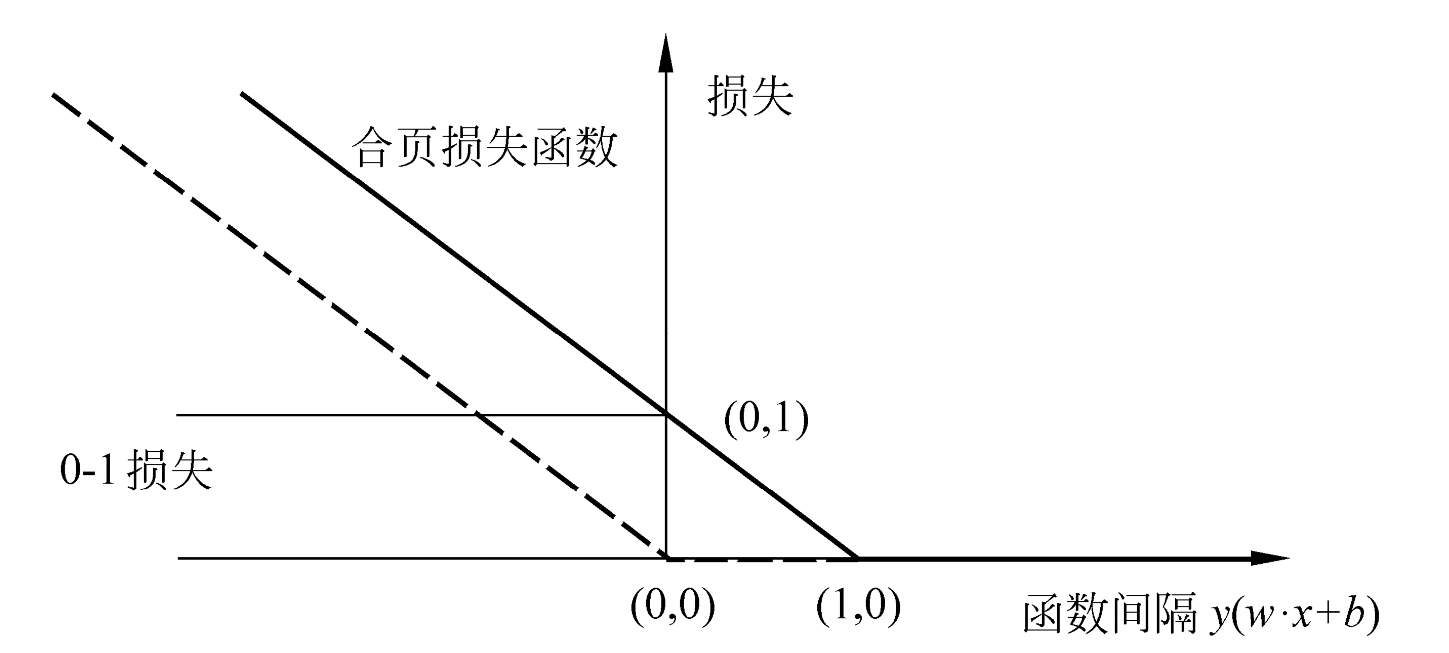
可以看到合页损失函数形似合页，故而得名。而0-1损失函数虽然是二分类问题真正的损失函数，但它不是连续可导的，对其进行优化是NP困难的，所以我们转而优化其上界（合页损失函数）构成的目标函数，这时上界损失函数又称为代理损失函数（surrogate loss function）。而对于感知机损失函数，直观理解为：当\((\bm{x}^{(i)}, y^{(i)})\)被正确分类时，损失是0，否则是\(-y(\bm{w}^{T}\bm{x} + b)\)。相比之下，合页损失函数不仅要求要正确分类，而且要确信度足够大时损失才是0，也就是说合页损失函数对学习效果有更高的要求。

合页损失函数处处连续，此时可以采用基于梯度的数值优化算法求解（梯度下降法、牛顿法等），在此不再赘述。不过，此时的目标函数非凸，不一定保证收敛到最优解。

算法

上一章我们尝试过在不借助SMO算法的情况下求解问题\((3)\)这一凸二次规划问题，结果发现收敛速度过慢。现在我们试试采用基于合页损失函数的梯度下降算法来直接求解参数\(\bm{w}\)和\(b\)。

from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from scipy.optimize import minimize
import numpy as np
import math
from copy import deepcopy
import torch
from random import choice

# 数据预处理
def preprocess(X, y):
    # 对X进行min max标准化
    for i in range(X.shape[1]):
        field = X[:, i]
        X[:, i] = (field - field.min()) / (field.max() - field.min())
    # 标签统一转化为1和-1
    y = np.where(y==1, y, -1)
    return X, y

class SVM():
    def __init__(self, lamb=0.01, input_dim=256):
        self.lamb = lamb
        self.w, self.b = np.random.rand(
            input_dim), 0.0

    # 注意一个批量的loss可并行化计算
    def objective_func(self, X, y):
        loss_vec = torch.mul(y, torch.matmul(X, self.w) + self.b)
        loss_vec = torch.where(loss_vec > 0, loss_vec, 0.)
        return 1/self.m * loss_vec.sum() + self.lamb * torch.norm(self.w)**2 

    def train_data_loader(self, X_train, y_train):
        # 每轮迭代随机采一个batch
        data = np.concatenate((X_train, y_train.reshape(-1, 1)), axis=1)
        np.random.shuffle(data)
        X_train, y_train = data[:, :-1], data[:, -1]
        for ep in range(self.epoch):
            for bz in range(math.ceil(self.m/self.batch_size)):
                start = bz * self.batch_size
                yield (
                    torch.tensor(X_train[start: start+self.batch_size], dtype=torch.float64),
                torch.tensor(y_train[start: start+self.batch_size],dtype=torch.float64))

    def test_data_loader(self, X_test):
        # 每轮迭代随机采一个batch
        for bz in range(math.ceil(self.m_t/self.test_batch_size)):
            start = bz * self.test_batch_size
            yield X_test[start: start+self.test_batch_size]

    def compile(self, **kwargs):
        self.batch_size = kwargs['batch_size']
        self.test_batch_size = kwargs['test_batch_size']
        self.eta = kwargs['eta'] # 学习率
        self.epoch = kwargs['epoch'] # 遍历多少次训练集

    def sgd(self, params):
        with torch.no_grad():
            for param in params:
                param -= self.eta*param.grad
                param.grad.zero_()

    def fit(self, X_train, y_train):
        self.m = X_train.shape[0] #样本个数
        # 主义w初始化为随机数，不能初始化为0
        self.w, self.b = torch.tensor(
            self.w, dtype=torch.float64, requires_grad=True), torch.tensor(self.b, requires_grad=True)
        for X, y in self.train_data_loader(X_train, y_train):
            loss_v = self.objective_func(X, y)
            loss_v.backward()
            # b有梯度，w没有梯度？
            self.sgd([self.w, self.b])
            # print(self.w, self.b)
        self.w = self.w.detach().numpy()
        self.b = self.b.detach().numpy()

    def pred(self, X_test):
        # 遍历测试集中的每一个样本
        self.m_t = X_test.shape[0]
        pred_list = []
        for x in self.test_data_loader(X_test):
            pred_list.append(np.sign(np.matmul(x, self.w) + self.b))
        return np.concatenate(pred_list, axis=0)

if __name__ == "__main__":
    X, y = load_breast_cancer(return_X_y=True)
    X, y = preprocess(X, y)
    X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.5, random_state=0)
    clf = SVM(lamb=0.01, input_dim=X_train.shape[1])
    clf.compile(batch_size=256, test_batch_size=1024, eta=0.001, epoch=1000) #定义训练参数
    clf.fit(X_train, y_train)
    y_pred = clf.pred(X_test)
    acc_score = accuracy_score(y_test, y_pred)
    print("The accuracy is: %.1f" % acc_score)

可以看到，效果不太好，哈哈，目前还在debug

The accuracy is: 0.6