SRM 558 SurroundingGame

题意：

给定一个网格，每个网格有选取代价和占据收益。每个点被占据，需要满足以下两个条件至少一个条件：1.被选取  2.邻近方格都被选取（有公共边被称为邻近）  不一定要占据所有方格，求最大收益。

输入说明
第一行两个数 n,m(n,m ≤ 20),表示矩形的长和宽。
接下来 n 行,每行是 m 个字符组成的字符串,描述投资的花费。
接下来 n 行,每行是 m 个字符组成的字符串,表示该格子的收益。
花费和收益按照一种奇葩的方式给出:
字符
数
‘0’-’9’
0-9
‘a’-’z’
10-35
‘A’-’Z’
36-61
输出说明
一个数,表示收益的和减去投资的和的最大值。
样例 1
2 2
21
12
21
12
答案:4
样例 2
2 2
ZZ
ZZ
11
11
答案: 0
样例 3
3 3
XXX
XXX
XXX
aaa
aZa
aaa
答案: 2
样例 4
2 4
asam
atik
123A
45BC
答案: 71
样例 5
98
IIIIIIII
IIWWWWII
IIWIIIII
IIWIIIII
IIWWWWII
IIIIIWII
IIIIIWII
IIWWWWII
IIIIIIII
IIIIIIII
II0000II
II0II0II
II0II0II
II0000II
II0II0II
II0II0II
II0000II
IIIIIIII
答案: 606

先黑白染色

源点S点连白点，汇点T点连黑点

现将所有利润加起来，显然要减去一部分花费和利润

我们求最小的使利润合法的要减去一部分花费和利润

然后转化为求最小割，设收益边和花费边

首先考虑几种情况

1.保留一个点的花费边，保留收益边(即不投资拿到利润)

那么此刻如果相邻有点没有割掉花费边，那么就会有流

2.割掉一个花费边，保留收益边(投资一个点)

3.割掉一个收益边，保留花费边(不投资该点)

只考虑前2中情况我们可以建出：

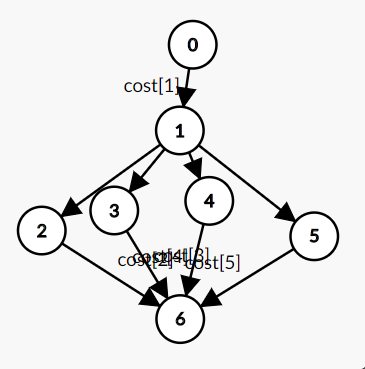
考虑第3种情况：

因为放弃这个格子的收益，代表着相邻的格子的收益必须要靠它自己的花费

于是有了如下建图

图片转自ZYYS

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<cmath>
 #include<queue>
 using namespace std;
 struct Node
 {
   int next,to,cap;
 }edge[];
 int head[],num=,inf=1e9,S,T,dist[],n,m,a[][],b[][],ans,tot,pre[][],nxt[][],col[][];
 char s1[][],s2[][];
 void add(int u,int v,int cap)
 {
   num++;
   edge[num].next=head[u];
   head[u]=num;
   edge[num].to=v;
   edge[num].cap=cap;
   num++;
   edge[num].next=head[v];
   head[v]=num;
   edge[num].to=u;
   edge[num].cap=;
 }
 bool bfs()
 {int i;
   queue<int>Q;
   for (i=S;i<=T;i++)
     dist[i]=-;
   dist[S]=;
   Q.push(S);
   while (Q.empty()==)
     {
       int u=Q.front();
       Q.pop();
       for (i=head[u];i;i=edge[i].next)
     {
       int v=edge[i].to;
       if (edge[i].cap==||dist[v]!=-) continue;
       dist[v]=dist[u]+;
       Q.push(v);
     }
     }
   if (dist[T]==-) return ;
   return ;
 }
 int dfs(int x,int flow,int des)
 {int i;
   if (x==des)  return flow;
   if (flow<=) return ;
   int res=,tmp;
   for (i=head[x];i;i=edge[i].next)
     {
       int v=edge[i].to;
       if (dist[v]==dist[x]+&&edge[i].cap)
     {
       tmp=dfs(v,min(edge[i].cap,flow-res),des);
       edge[i].cap-=tmp;
       edge[i^].cap+=tmp;
       res+=tmp;
       if (res==flow) return res;
     }
     }
   return res;
 }
 int Maxflow()
 {
   int as=;
   while (bfs())
     {
       int a=;
       while (a=dfs(S,inf,T)) as+=a;
     }
   return as;
 }
 int main()
 {int i,j;
   cin>>n>>m;
   for (i=;i<n;i++)
     {
       scanf("%s",s1[i]);
     }
   for (i=;i<n;i++)
     {
       scanf("%s",s2[i]);
     }
   for (i=;i<=n;i++)
     {
       for (j=;j<=m;j++)
     {
       if (s1[i-][j-]>=''&&s1[i-][j-]<='')
         a[i][j]=s1[i-][j-]-'';
       else if (s1[i-][j-]>='a'&&s1[i-][j-]<='z')
         a[i][j]=s1[i-][j-]-'a'+;
       else a[i][j]=s1[i-][j-]-'A'+;
     }
     }
     for (i=;i<=n;i++)
     {
       for (j=;j<=m;j++)
     {
       if (s2[i-][j-]>=''&&s2[i-][j-]<='')
         b[i][j]=s2[i-][j-]-'';
       else if (s2[i-][j-]>='a'&&s2[i-][j-]<='z')
         b[i][j]=s2[i-][j-]-'a'+;
       else b[i][j]=s2[i-][j-]-'A'+;
       ans+=b[i][j];
     }
     }
     S=;tot=;
     for (i=;i<=n;i++)
       {
     for (j=;j<=m;j++)
       {
         pre[i][j]=++tot;nxt[i][j]=++tot;
         col[i][j]=(i+j)&;
       }
       }
     T=++tot;
     for (i=;i<=n;i++)
       {
     for (j=;j<=m;j++)
       {
         if (col[i][j]==)
           {
         add(S,pre[i][j],a[i][j]);
         add(pre[i][j],nxt[i][j],b[i][j]);
         if (i-)
           add(pre[i][j],nxt[i-][j],inf),add(nxt[i][j],pre[i-][j],inf);
         if (i<n)
           add(pre[i][j],nxt[i+][j],inf),add(nxt[i][j],pre[i+][j],inf);
         if (j-)
           add(pre[i][j],nxt[i][j-],inf),add(nxt[i][j],pre[i][j-],inf);
         if (j<m)
           add(pre[i][j],nxt[i][j+],inf),add(nxt[i][j],pre[i][j+],inf);
           }
         else
           {
         add(pre[i][j],T,a[i][j]);
         add(nxt[i][j],pre[i][j],b[i][j]);
           }
       }
       }
     cout<<ans-Maxflow();
 }