Codeforces #541 (Div2) - D. Gourmet choice（拓扑排序+并查集）

Problem   Codeforces #541 (Div2) - D. Gourmet choice

Time Limit: 2000 mSec

Problem Description

Input

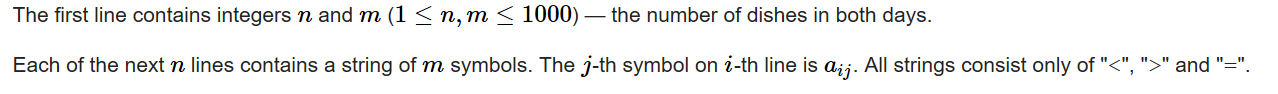
Output

The first line of output should contain "Yes", if it's possible to do a correct evaluation for all the dishes, or "No" otherwise.

If case an answer exist, on the second line print nn integers — evaluations of dishes from the first set, and on the third line print mm integers — evaluations of dishes from the second set.

Sample Input

3 4
>>>>
>>>>
>>>>

Sample Output

Yes
2 2 2
1 1 1 1

题解：一看就是拓扑排序，一通敲之后发现第三个样例过不去，原因是没有妥善处理等号的问题，其实很容易解决，相等的节点缩成一个，用并查集很容易实现，之后再拓扑排序就没问题了。

 #include <bits/stdc++.h>

 using namespace std;

 #define REP(i, n) for (int i = 1; i <= (n); i++)
 #define sqr(x) ((x) * (x))

 const int maxn =  + ;
 const int maxm =  + ;
 const int maxs =  + ;

 typedef long long LL;
 typedef pair<int, int> pii;
 typedef pair<double, double> pdd;

 const LL unit = 1LL;
 const int INF = 0x3f3f3f3f;
 const LL mod = ;
 const double eps = 1e-;
 const double inf = 1e15;
 const double pi = acos(-1.0);

 int n, m;
 string str[maxn];
 vector<int> G[maxn];
 int deg[maxn], ans[maxn];
 int fa[maxn];
 int Min, tot;

 int findn(int x)
 {
     return x == fa[x] ? x : fa[x] = findn(fa[x]);
 }

 void merge(int x, int y)
 {
     int fx = findn(x), fy = findn(y);
     if (fx != fy)
     {
         fa[fx] = fy;
     }
 }

 bool toposort()
 {
     queue<int> que;
     Min = ;
     int cnt = ;
     for (int i = ; i < n + m; i++)
     {
         if (findn(i) == i && !deg[i])
         {
             que.push(i);
             cnt++;
             ans[i] = ;
         }
     }
     while (!que.empty())
     {
         int u = que.front();
         que.pop();
         for (auto v : G[u])
         {
             int fv = findn(v);
             if (fv == v)
             {
                 deg[fv]--;
                 if (!deg[fv])
                 {
                     cnt++;
                     que.push(fv);
                     ans[fv] = ans[u] - ;
                     Min = min(ans[fv], Min);
                 }
             }
         }
     }
     return cnt == tot;
 }

 void output()
 {
     cout << "YES" << endl;
     for (int i = ; i < n; i++)
     {
         cout << ans[findn(i)] - Min + ;
         if (i != n - )
         {
             cout << " ";
         }
         else
         {
             cout << endl;
         }
     }
     for (int i = n; i < n + m; i++)
     {
         cout << ans[findn(i)] - Min + ;
         if (i != n - )
         {
             cout << " ";
         }
         else
         {
             cout << endl;
         }
     }
 }

 void premanagement()
 {
     for (int i = ; i < n + m; i++)
     {
         if (findn(i) == i)
         {
             tot++;
         }
     }
 }

 int main()
 {
     ios::sync_with_stdio(false);
     cin.tie();
     //freopen("input.txt", "r", stdin);
     //freopen("output.txt", "w", stdout);
     cin >> n >> m;
     for(int i = ; i < n + m; i++)
     {
         fa[i] = i;
     }
     for (int i = ; i < n; i++)
     {
         cin >> str[i];
     }
     for (int i = ; i < n; i++)
     {
         for (int j = ; j < m; j++)
         {
             if (str[i][j] == '=')
             {
                 merge(i, n + j);
             }
         }
     }
     for (int i = ; i < n; i++)
     {
         for (int j = ; j < m; j++)
         {
             if (str[i][j] == '>')
             {
                 int fi = findn(i), fj = findn(n + j);
                 G[fi].push_back(fj);
                 deg[fj]++;
             }
             else if (str[i][j] == '<')
             {
                 int fi = findn(i), fj = findn(n + j);
                 G[fj].push_back(fi);
                 deg[fi]++;
             }
         }
     }
     premanagement();
     bool ok = toposort();
     if (!ok)
     {
         cout << "NO" << endl;
     }
     else
     {
         output();
     }
     return ;
 }