AI算法：1. 决策树

今天，我们介绍的机器学习算法叫决策树。

跟之前一样，介绍算法之前先举一个案例，然后看一下如何用算法去解决案例中的问题。

我把案例简述一下：某公司开发了一款游戏，并且得到了一些用户的数据。如下所示：

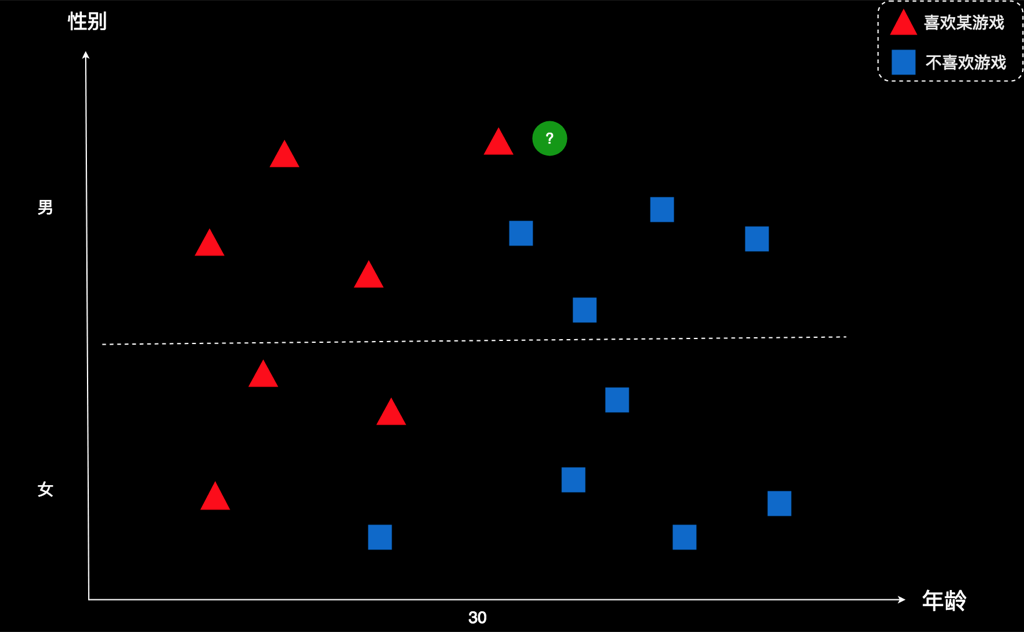
图上每个图形表示一个用户，横坐标是年龄，纵坐标是性别。红色表示该用户喜欢这款游戏，蓝色表示该用户不喜欢这款游戏。比如，右下角这个蓝色方框，代表的是一个五六十岁的女士。蓝色表示她不喜欢这款游戏。再比如，左上角的红色三角形，代表的是一个十来岁的男孩。红色表示他喜欢这款游戏。

现在有个新用户，用绿色所示。这家公司想知道：这个新用户会不会喜欢这款游戏？

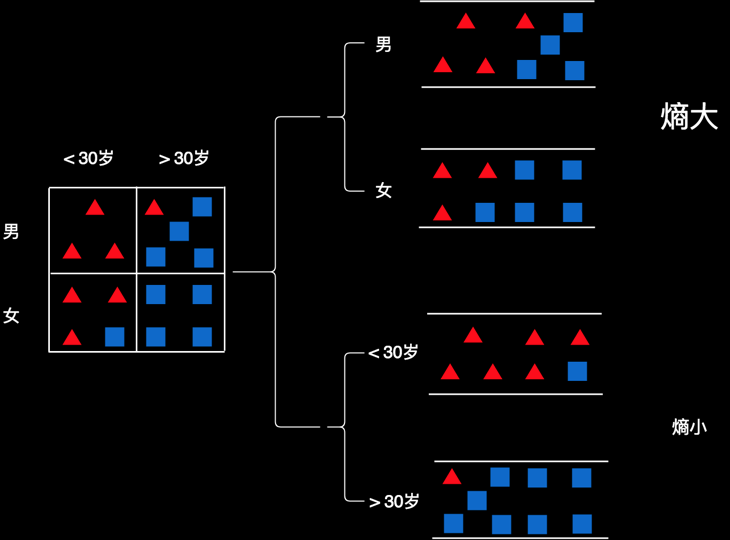
仅从图上看，我们很难一眼就做出有效的判断。我们不妨先把用户的属性梳理一下，然后对用户进行归类。按照性别和年龄两个维度来分，可以制作出一个这样的表格。我们把每一个用户都按条件放到相应的格子里，如图所示：

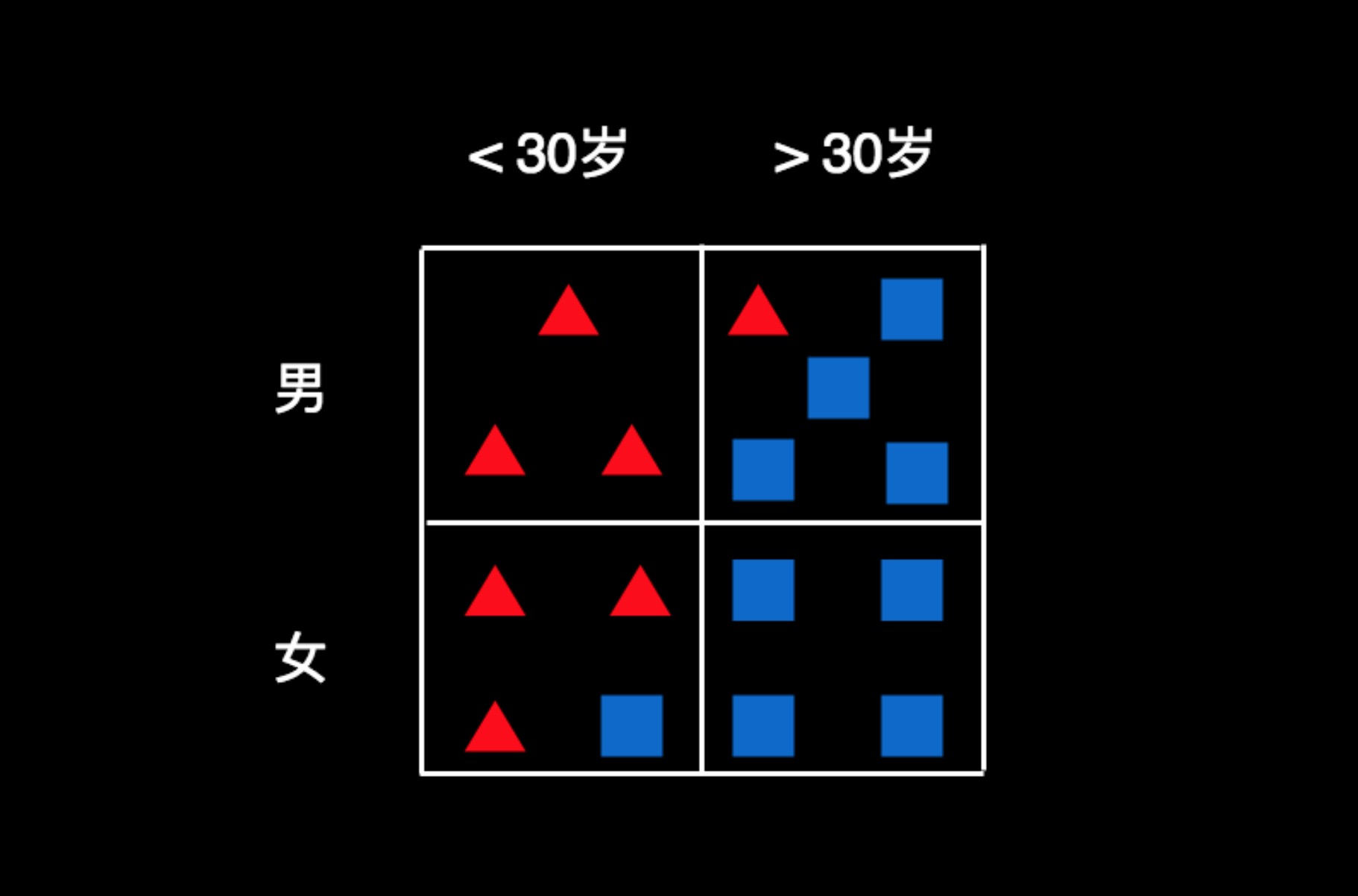
小于30岁且性别为男的用户都在第一个格子里，总共有3个人，且全部喜欢玩游戏；30以上的且性别为女的用户都在右下角的格子里，总共有4个人，且都不玩这款游戏。其他的人，有的喜欢玩游戏，有的不喜欢。

我们可以再创建一颗树，用于判断这些人的偏好。比如，我们先用性别作判断条件，把人分成“男”和“女”两份。然后在每一份里面，再用年龄把他们再分成两份。

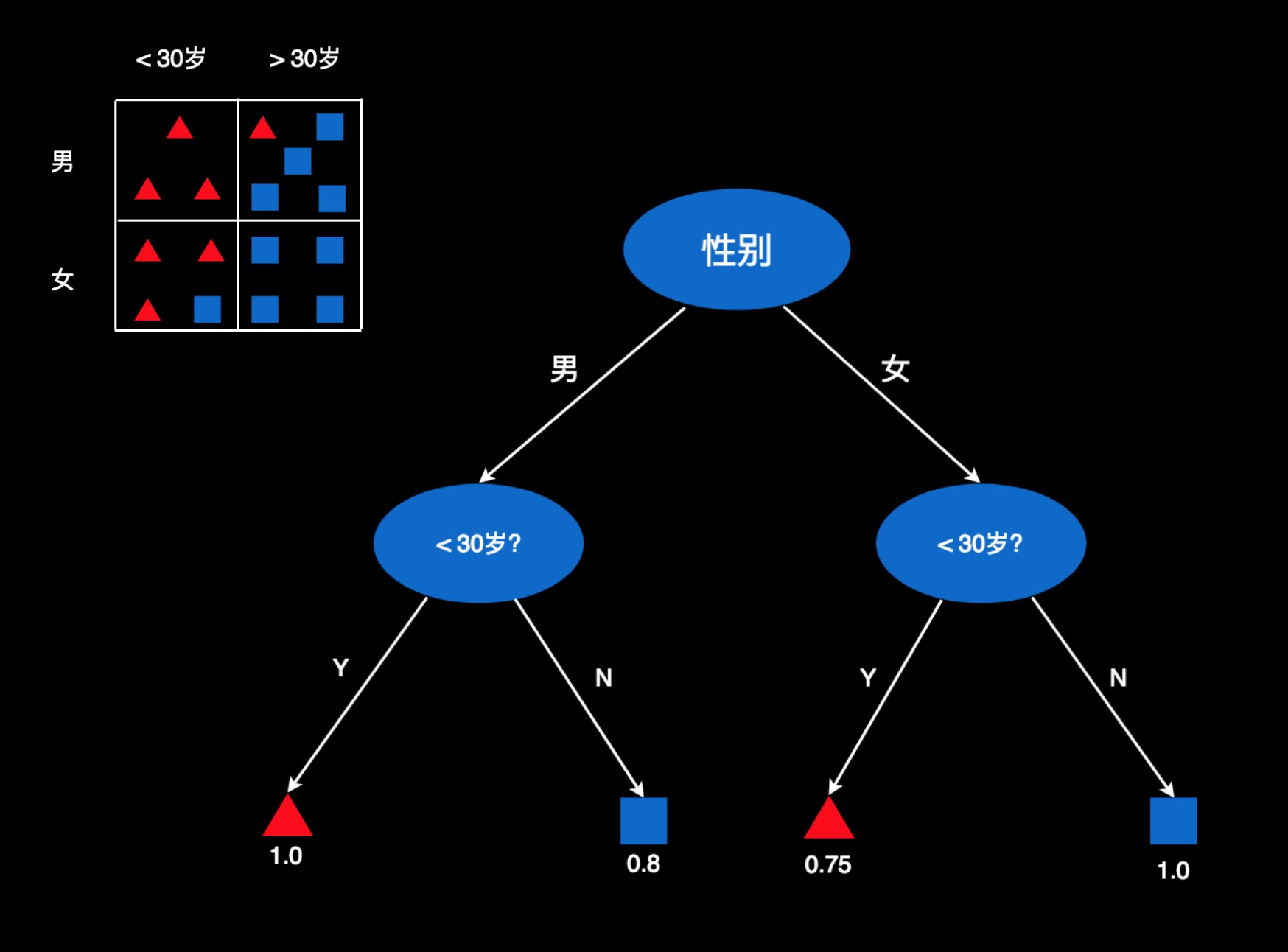
图中用椭圆形代表判断条件，比如性别是什么，是否小于30岁。箭头是判断结果，比如男在左侧，女性在右侧。小于30岁的在左侧，大于30岁的在右侧。

最底下是这棵树的叶子节点，每一个叶子节点就是一个判断结果。对于性别为男且小于30岁的用户，判断结果就在最左侧那片叶子上。这个叶子节点对应的是表格中第一个格子的数据。那里100%的用户都是红色，所以，这用红色的三角表示。数值为1.0，表示红色用户的占比为100%，或者红色用户的概率为100%。

第二个叶子节点为蓝方块，它对应第二个格子中的数据。符合这些条件的用户，有80%的人是蓝色。所以，这里是蓝色，且数值为0.8。

其它以此类推。红色0.75表示75%的用户是红色，蓝色1.0，表示100%的人蓝色。

如果来了新的用户，就把他的属性往这棵树上套，找到他所在的叶子节点，然后根据叶子节点的颜色和数字来判断他的偏好。比如，一个15岁的小伙子，我们看一下，他应该在这棵树的哪个位置。因为是男性，所以在左半部分。有知道他是15岁，小于30岁，所以在他位于左下角的叶子。这个叶子为红色，且数值等于1.0。即喜欢这款游戏的概率为100%。于是，就判断他非常可能喜欢这款游戏。再比如，来了一个25岁的女士。因为是女性，所以在又半个树上。年龄25岁，小于30，所以会会定位在第三个叶子。这个叶子是红色，且数值等于0.75。因此，我们判断他喜欢这款游戏的概率是75%，或者说她有可能喜欢这款游戏。若是一个45岁的女士，往树上套，就会定位在第四个叶子，颜色为蓝色，数值为1.0。因此，她不喜欢这款游戏的概率为100%，或者说喜欢游戏的概率为0。

这棵树就是一颗决策树。

我们同样可以创建另一棵树，把条件的顺序颠倒一下，第一层是年龄，第二层是性别。

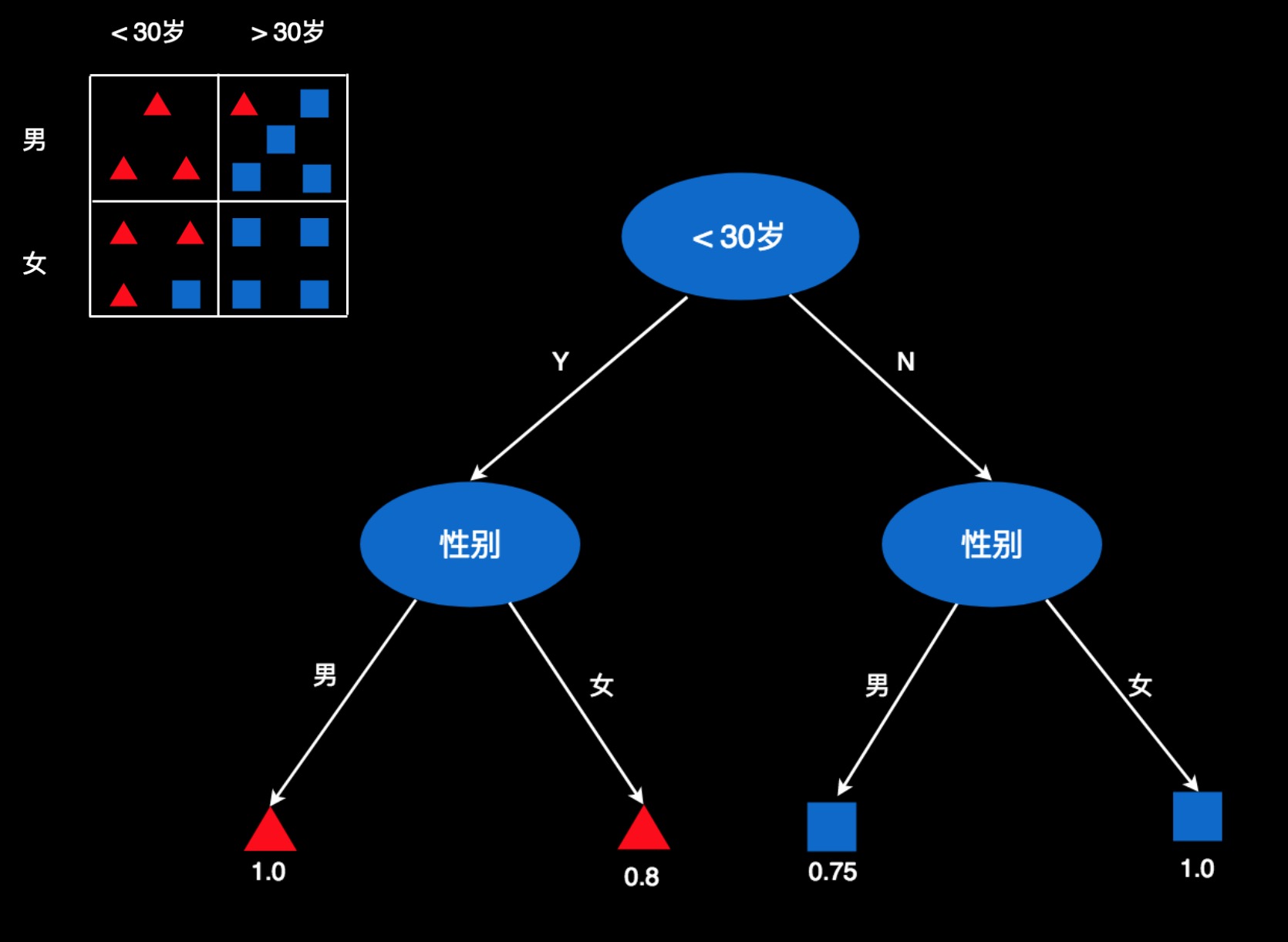
这两棵树的叶子都是一样的，只是顺序不一样而已。所以用这两棵树的做判断，结果是一样的。不过，这两棵树不是等价的！

它们的不同之处在于，“性别”和“年龄”这两个属性的重要性不一样！

重要性是什么意思？

可以这么想象一下：如果只让你选择一个属性，你选择哪个属性。或者说只允许选择一个属性的时候，选哪个属性会让你的决策更准确一些？我们不妨实验一下。

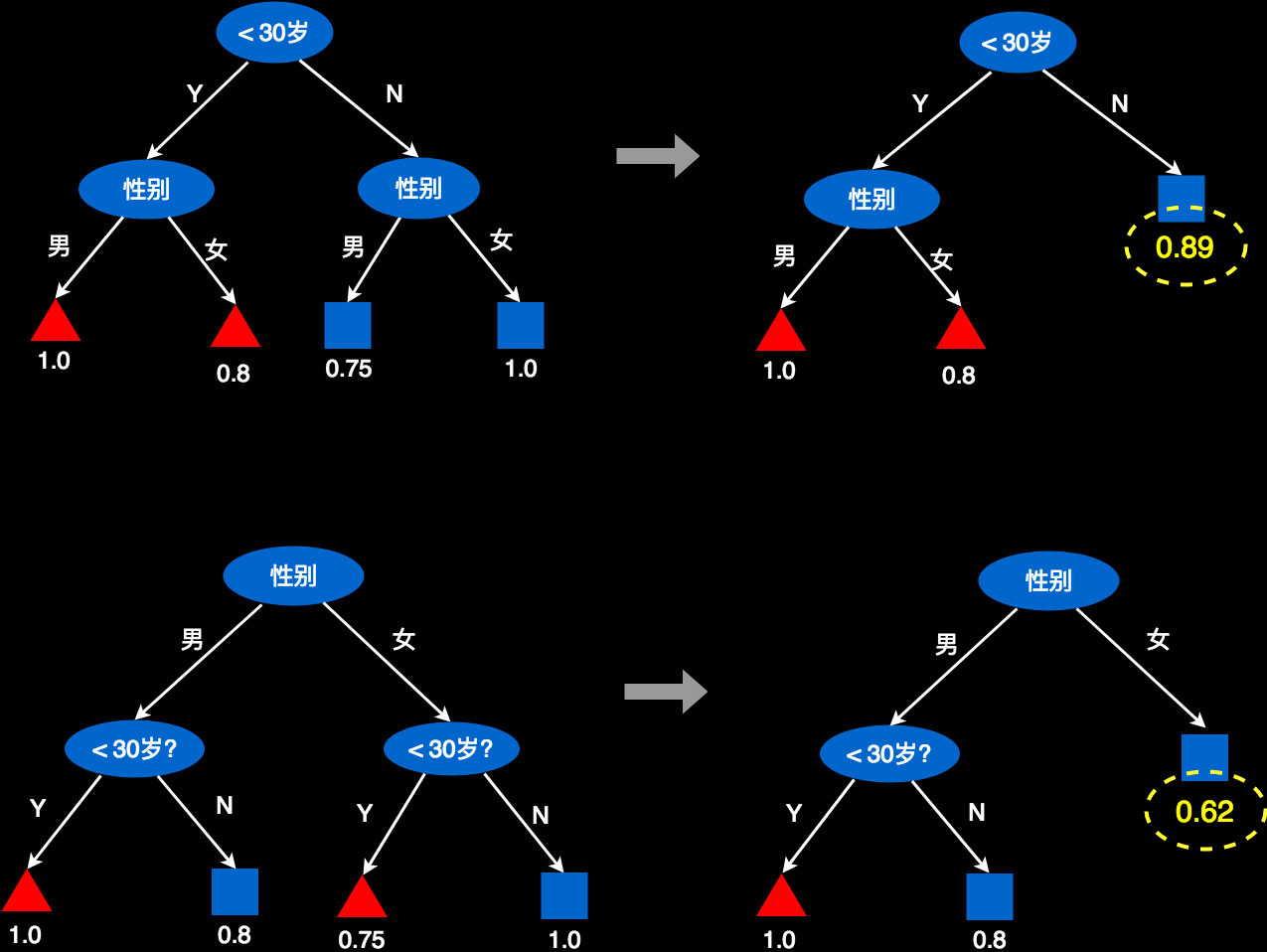
1. 假设我们只能用“性别”属性。

我们用性别来判断，发现男性用户里，有一半是红色，一半是蓝色。所以，我们无法判断，男性用户应该是红色好还是蓝色好。发现女性用户里，有3个红色，有5个蓝色。我们隐约可以做一个判断：“女性用户不大喜欢玩这款游戏”。但是，你做这个判断的时候，会底气不足，毕竟还有3个女性是喜欢玩的。

2. 假设我们只能用“年龄”这个属性。

我们会发现，小于30岁的用户总共有7个，其中有6个是红色的，占比85.7%。大于30岁的用户总共有9个，其中有8个是蓝色的，占比89%。于是，我们可以大胆的判断：“小于30岁的用户更喜欢玩游戏，大于30岁的用户不喜欢玩。”你做这个判断时，底气十足，铿锵有力！

凭直觉，你就会觉得“年龄”这个属性更重要！

没错，你的直觉是对的！

原因是，用了“性别”后，数据仍然混乱不清；而用了“年龄”这个属性后，数据变得确定起来。

关于确定性或不确定性的程度，信息论里用一个叫做“熵”的词来表示。“熵”这个词原本是热力学里的一个概念，用于表示热力学系统的无序程度。熵越大表示越无序，熵越小表示越有序。1948年，香浓把它引入到信息论里，并给出了信息熵的计算公式。信息熵越大，不确定性越大；熵越小，不确定性越小。这个被认为是20世纪最重要的贡献之一！

上图中，若数据中增加了“性别”属性进行分类，用户是那种颜色仍然不是很确定，所以熵值比较大。若数据中增加了“年龄”属性进行分类，用户的颜色基本就确定了，所以熵值就小。

因此：一个属性的重要性，可以用它所产生的熵值大小来判断。使得熵值变的更小的属性，重要性更高！

熵是有一个精确的公式，具体就不在这里写了。有机会的话，我会在以后的高级课程里讲。

既然熵可以计算，那属性的重要性就可以计算。我们把所有属性产生熵计算一遍，从小到大排序，最小熵值对应的属性就是最重要的。我们把最重要的属性放到决策树最上面的节点。

然后在每个分支上，计算剩余属性中最重要的属性，放到二级节点。以此类推。

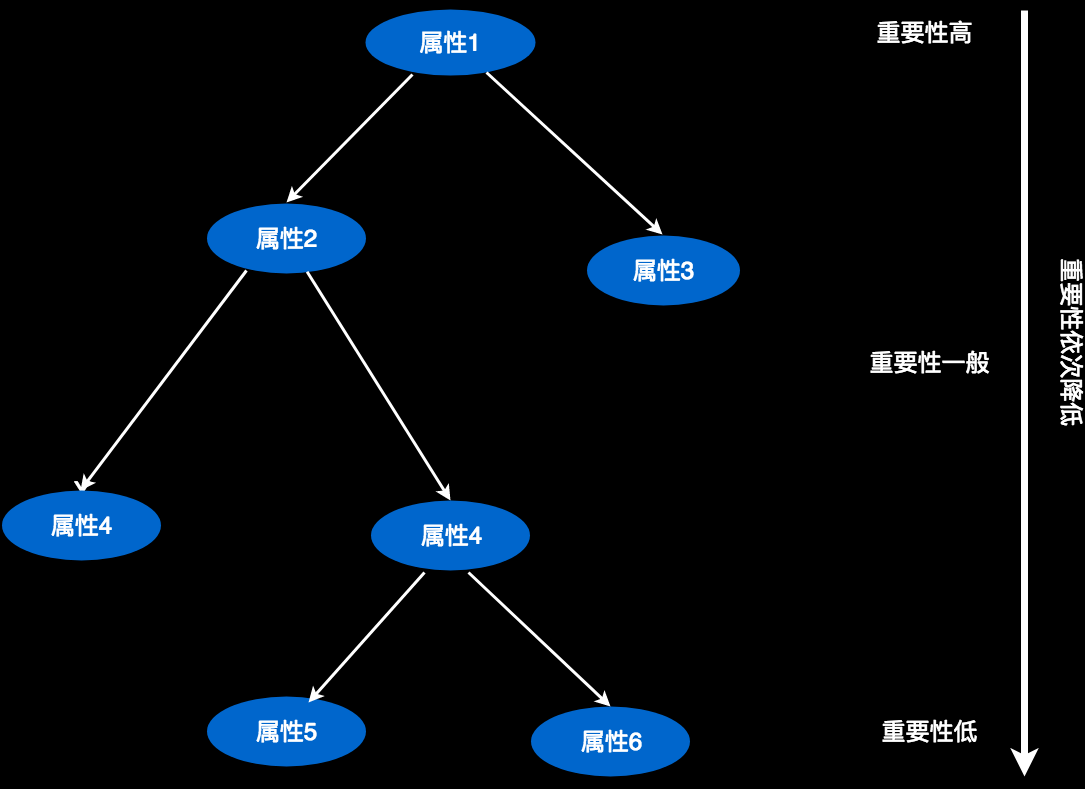
当我们有很多属性的时候，放在最底下的属性，其影响力可能微小到忽略不计，我们就可以不要它们，这样决策树的结构也就很精简,只包含重要属性。在有些情况下，这样对枝叶的裁剪可以有效的避免过拟合。关于什么叫“过拟合”，以后有机会再讲，有兴趣的同学也可以自己查一查。

对于上面的两个树，我们可以尝试裁剪一下。如下图所示。以年龄为根的树，通过裁剪，仍然可以有很好的预测准确率，因为右侧被裁剪后，仍然有89%的预测准确率，这个概率已经足够高。而对以性别为根对树进行裁剪，就会有些问题。因为右侧叶子仅有62%的预测准概率。可以看出来“年龄”做根更好一些。

下面是一段伪代码，createBranch方法用于创建决策树的分支，它是一个递归的结构。

createBranch(){

    检测数据集中的每个子项是否属于同一分类

    if  是同一分类{

       return 分类标签

    }else{

        寻找划分数据集的最好特征  

        划分数据集    

        创建分支节点        

        for 每个划分的子集{            

            调用函数createBranch并增加返回结果到分支节点中  

        } 

        return 分支节点

    } 

}

参考原文连接： https://my.oschina.net/stanleysun/blog/167035