洛谷P1936 水晶灯火灵 P1775 古代人的难题_NOI导刊2010提高（02）【重题请做P1936】

首先我要说明，此题（古代人的难题）与水晶灯火灵是一模一样的！

古代人的难题

(File IO): input:puzzle.in output:puzzle.out

时间限制: 1000 ms  空间限制: 60000 KB  具体限制

Time to Submit: 01:57:40

题目描述

门打开了， 里面果然是个很大的厅堂。但可惜厅堂内除了中央的一张羊皮纸和一根精致的石笔，还有周围几具骷髅外什么也没有。 难道这就是王室的遗产？ 小 FF 不信，他仔细阅读了羊皮纸上的内容后发现，里面书写的古代人一直没能解出的难题， 解除这道题目的人只要将答案用石笔写到这张羊皮纸上就能到达王室的宝藏室了。而当小 FF 拿起石笔后，刚刚打开的巨石门突然关上了。 这时小 FF 意识到原来那几具骷髅是在他之前到这里的冒险者，恐怕是因为没能破解这道题而困死在这里了。 小 FF 越想越害怕， 急忙联系到了你，为了能保命，他甚至愿意和你五五分……看来你不得不再次帮他了。 羊皮纸上的问题如下：

已知 x， y 为整数，且满足以下两个条件：

1. x, y ϵ [1..k], 且x，y，k ϵ Z；

2. （x^2 – xy – y^2）^2 = 1

给你一个整数 k， 求一组满足上述条件的 x， y 并且使得 x^2 + y^2 的值最大。

当小 F 得到答案后， 用石笔将答案书写在羊皮纸上，那么就能到达王室的遗产所在地了。

输入

一个整数 k

输出

输出文件仅一行，两个整数；

两个整数分别表示 x 和 y。x, y 之间用一个空格隔开。

样例输入

1995

样例输出

1597 987

数据范围限制

对于 30%的数据： 2<=k<=10^4.

对于 100%的数据： 2<=k<=10^18.

提示

Z是数学里面整数集合符号，  即x y k都是整数

Solution(P1775&P1936)

悄悄地打个表（其实就是在暴力枚举模拟的过程）

table_code

#include<bits/stdc++.h>
using namespace std;
unsigned long long k;
int main()
{
    freopen("table.txt","w",stdout);
//    cin>>k;
    int maxans=,maxx=,maxy=;
    for(k=;k<=;k++)
    {
 
    for(int x=;x<=k;x++)
    for(int y=;y<=x;y++)
    {
        if((x+y)*(x-y)==x*y+||(x+y)*(x-y)==x*y-)
        if(maxans<x*x+y*y)
        {
            maxans=max(maxans,x*x+y*y);
            maxx=x;
            maxy=y;
        }
    }
    cout<<k<<" "<<maxx<<" "<<maxy<<endl;}
    return ;
}

table.txt

k x y

table.txt

哈，这不是熟悉的斐波那契数列兄弟嘛

那么问题就变成了：

已知k，求x，y。

其中x，y属于斐波那契数列相邻了两项且x>y（P1936 水晶灯火灵 中是m<n）

使得k>=x&&k<x+y

//文末有证明！

Code(P1775)

 #include<bits/stdc++.h>
 using namespace std;
 unsigned long long k;
 void make()
 {
     int i=;
     unsigned long long x=,y=,t,l=,r;
     while(true)
     {
         t=x;
         x=x+y;
         y=t;
         if(k>=x&&k<x+y)
         {
             cout<<x<<" "<<y;
             return;
         }
     }
     return;
 }
 int main()
 {
 //    freopen("puzzle.in","r",stdin);
 //    freopen("puzzle.out","w",stdout);
     cin>>k;
     make();
     return ;
 }
 /*
 1. x, y sy [1..k], 且x，y，k sy Z；
 2. （x^2 - xy - y^2）^2 = 1
 给你一个整数 k，
 求一组满足上述条件的 x， y
 并且使得 x^2 + y^2 的值最大。
 
 */

也可以利用打的表（修改了一下）

 #include<bits/stdc++.h>
 using namespace std;
 unsigned long long k;
 unsigned long long table[]={
 ,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,
 ,,,,,,,,,,,,,,,
 ,,,,,,,,,,,,
 ,,,,,,,,,,
 ,,,,,,,,,
 ,,,,,,,,
 ,,};
 int main()
 {
 //    freopen("puzzle.in","r",stdin);
 //    freopen("puzzle.out","w",stdout);
     cin>>k;
     for(int i=;i<=;i++)
         if(k>=table[i]&&k<table[i+])
         {
             cout<<table[i]<<" "<<table[i-];
             break;
         }
     return ;
 }

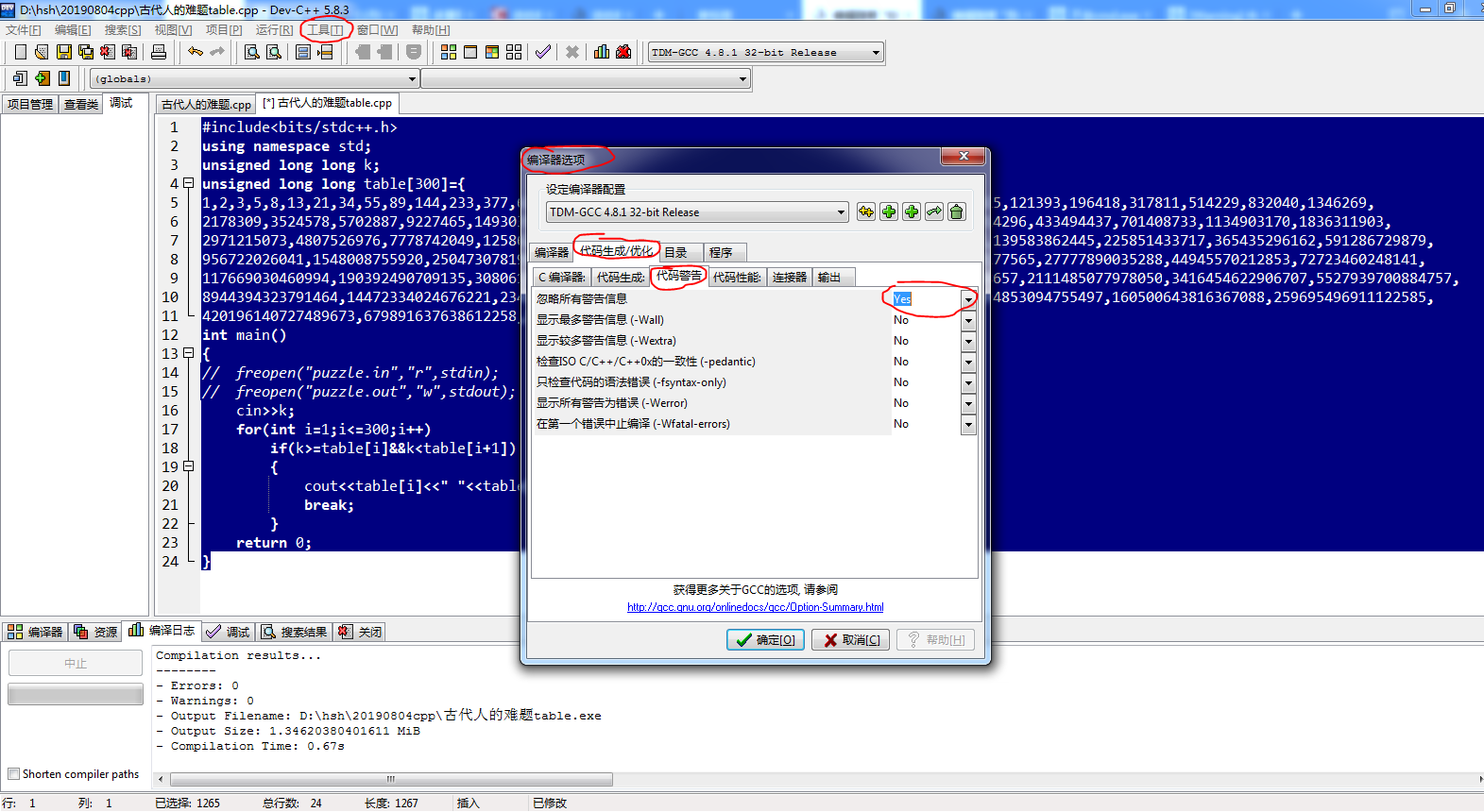
但是请注意，上面这种方法请在 工具 -> 编译选项 -> 代码生成/优化 -> 代码警告 中把“忽略所有警告信息” 设为“Yes”

Code(P1936)

 #include<bits/stdc++.h>
 using namespace std;
 unsigned long long k;
 void make()
 {
     int i=;
     unsigned long long x=,y=,t,l=,r;
     while(x<k*)
     {
         t=x;
         x=x+y;
         y=t;
         if(k>=x&&k<x+y)
         {
             cout<<"m="<<y<<endl<<"n="<<x;
             return;
         }
     }
     return;
 }
 int main()
 {
     cin>>k;
     make();
     return ;
 }
 /*
 1. x, y sy [1..k], 且x，y，k sy Z；
 2. （x^2 - xy - y^2）^2 = 1
 给你一个整数 k，
 求一组满足上述条件的 x， y
 并且使得 x^2 + y^2 的值最大。
 
 */

证明

本文提供两种证明方法。敬请过目~

证明（P1775）

(x^2 - xy - y^2)^2

= (y^2 + xy - x^2)^2

= [(x+y)^2 - xy - 2*x^2]^2

=[(x+y)^2 - (x+y)*x - x^2]^2

由上式可知， 如果x, y 满足条件2， 那么x+y, y 也满足条件2。

那么Fibomacci 中小于等于k 的最大两个相邻的数即为试题所需的解。

证明（P1936）

记f(n,m)=(n^2-mn-m^2)^2

则有f(m+n,m)=[(m+n)^2-n(m+n)-n^2]^2=(m^2+mn-n^2)^2=(n^2-mn-m^2)^2=f(n,m)

易得f(1,1)=1

故1=f(1,1)=f(2,1)=f(3,2)=...