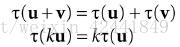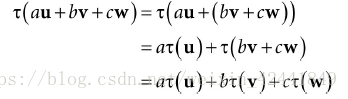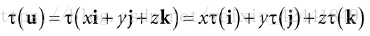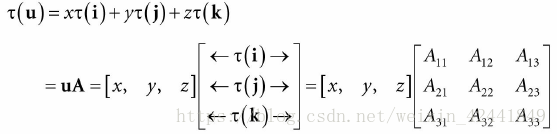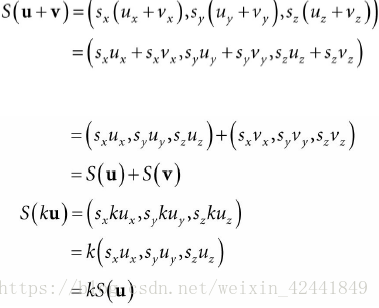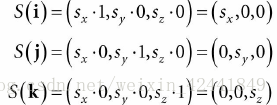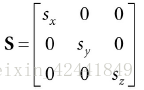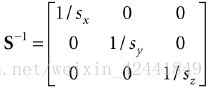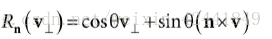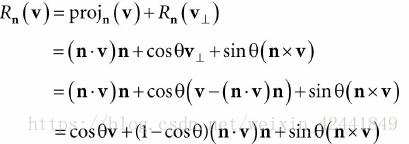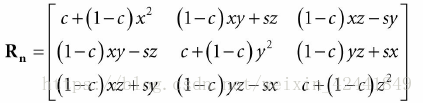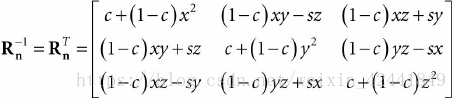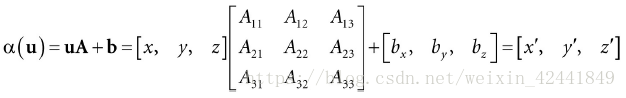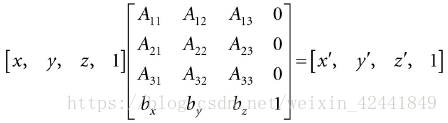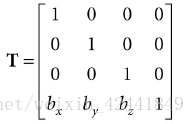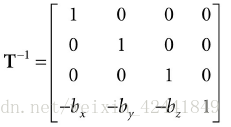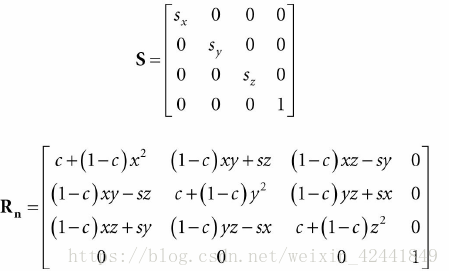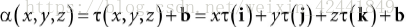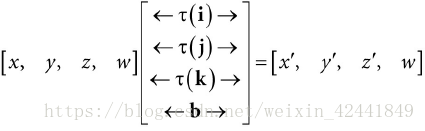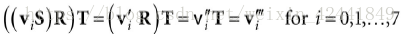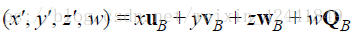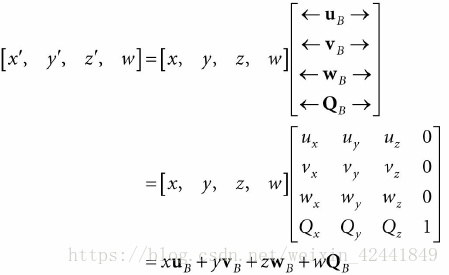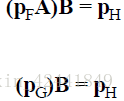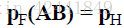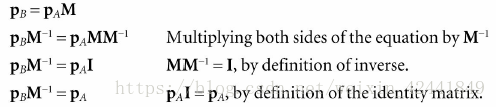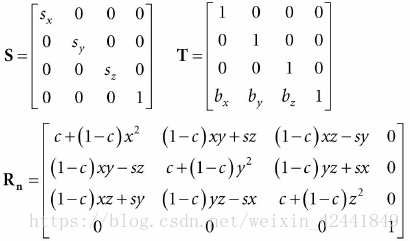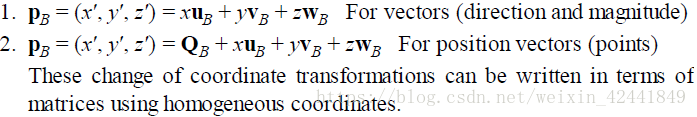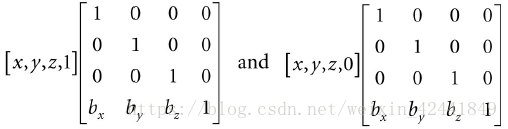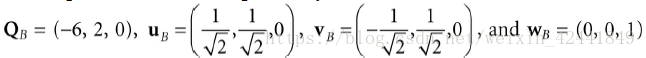Introduction to 3D Game Programming with DirectX 12 学习笔记之 --- 第三章：变换

原文:Introduction to 3D Game Programming with DirectX 12 学习笔记之 --- 第三章：变换

学习目标

1. 理解如何用矩阵表示线性变换和仿射变换；
2. 学习在坐标系中缩放，旋转和移动几何体；
3. 学习利用矩阵的乘法合并几个变换矩阵；
4. 学习如何在坐标系之间转换，并且表示为转换矩阵；斜体样式
5. 学习如何利用DirectX Math库提供的方法构造转换矩阵。

---

---

1 线性转换

---

1.1 线性转换的定义

现在有方程τ(v)=τ(x,y,z)=τ(x1,y1,z1)τ(v) = τ(x, y, z) = τ(x^1, y^1, z^1)τ(v)=τ(x,y,z)=τ(x1,y1,z1)，当且仅当它满足下列属性的时候：



我们称它为一个线性变换。其中u和v是3D向量，k是标量。

例如定义τ(v)=τ(x,y,z)=τ(x2,y2,z2)τ(v) = τ(x, y, z) = τ(x^2, y^2, z^2)τ(v)=τ(x,y,z)=τ(x2,y2,z2)；τ(1, 2, 3) = (1, 4, 9)；这个方程不是线性的，因为如果k = 2和u = (1, 2, 3)：τ(ku) = τ(2, 4, 6) = (4, 16, 36)，但是kτ(u) = 2(1, 4, 9) = (2, 8, 18)

所以不符合性质2，如果它是线性的，它应该符合：

---

1.2 矩阵表示

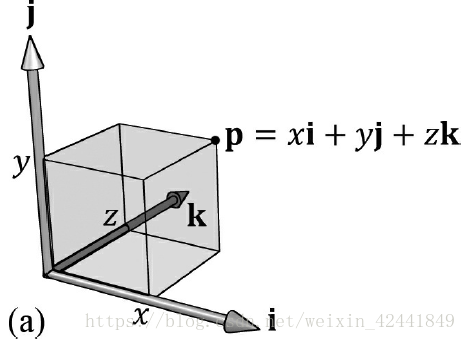
令u = (x, y, z)我们可以把它写成如下形式：

u=(x,y,z)=xi+yj+zk=x(1,0,0)+y(0,1,0)+z(0,0,1)u = (x, y, z) = xi + yj + zk = x(1, 0, 0) + y(0, 1, 0) + z(0, 0, 1)u=(x,y,z)=xi+yj+zk=x(1,0,0)+y(0,1,0)+z(0,0,1)

其中向量i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1)，是坐标系轴方向的单位向量，它们分别被称为R3R^3R3的标准基本向量，现在令τ为一个线性变换，它具备下面性质：



那么它可以被写成向量和矩阵相乘的形式：



其中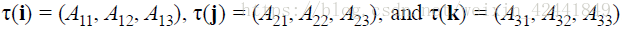，我们称矩阵A是线性变换τ的矩阵表现。

---

1.3 缩放

我们使用下面的公式来定义缩放：

S(x,y,z)=(sxx,syy,szz)S(x, y, z) = (s_xx, s_yy, s_zz)S(x,y,z)=(sx​x,sy​y,sz​z)

它是物体在x轴方向缩放sxs_xsx​倍，在y轴和z轴同理；我们现在要证明S 是一个线性转换：



为了得到矩阵表现，我们把S应用到每个标准基本向量中，然后把结果放到矩阵的每一行中：



所以S的矩阵表现为：



我们称这个矩阵为缩放矩阵，其逆矩阵为：

---

1.4 旋转

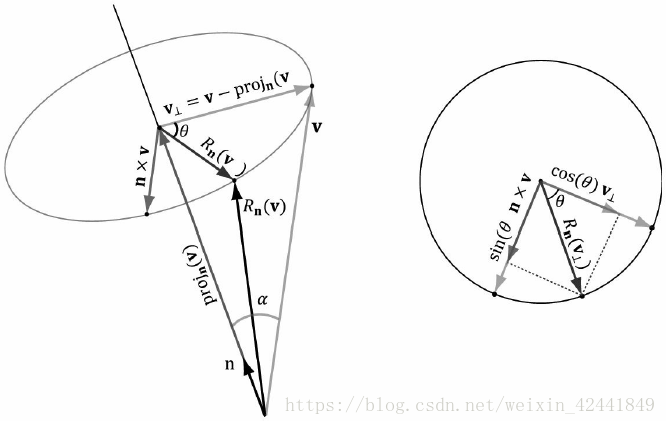
这一节我们描述将一个向量V关于轴n旋转θ角度；其中角度是当我们看向n轴时的顺时针方向，并且||n|| = 1：



首先将v分解为2部分：平行于n（projn(v)proj_n(v)projn​(v)）和垂直于n（perpn(v)perp_n(v)perpn​(v)）；因为n是一个单位向量，所以projn(v)=(n⋅v)nproj_n(v) = (n \cdot v)nprojn​(v)=(n⋅v)n；值得注意的是projn(v)proj_n(v)projn​(v)是平行于n的，它在旋转的过程中不变，所以我们只需要关注垂直那部分如果旋转，即旋转向量的结果就等于：Rn(v)=projn(v)+Rn(perpn(v))R_n(v) = proj_n(v) + R_n(perp_n(v))Rn​(v)=projn​(v)+Rn​(perpn​(v))；

为了计算Rn(perpn(v))R_n(perp_n(v))Rn​(perpn​(v))，我们在旋转的平面上构建一个2D坐标系，首先使用perpn(v)perp_n(v)perpn​(v)为第一个引用向量，为了得到第二个引用向量，我们使用叉积得到一个同时垂直于v和n的向量n×vn \times vn×v，根据之前第一章练习14证明的公式（α是n和v之间的夹角）：

∣∣n×v∣∣=∣∣n∣∣∣∣v∣∣sina=∣∣v∣∣sina=∣∣∣perpn(v)∣||n \times v|| = ||n||||v||sina = ||v||sina = |||perp_n(v)|∣∣n×v∣∣=∣∣n∣∣∣∣v∣∣sina=∣∣v∣∣sina=∣∣∣perpn​(v)∣

所以所有引用向量的长度都是一样的，并且都是同一个园的半径，现在我们可以建立起他们之间的联系，得到公式如下：

进一步，可以得到旋转公式：

然后根据1.2中的公式，将上述线性变换转成矩阵（其中c为cosθ，s为sinθ）：

旋转矩阵有一个有趣的性质，它每一行的向量都是单位长度，并且互相垂直，所以它的行向量们是标准正交的；一个矩阵的行向量们标准正交的话，该矩阵称为标准正交矩阵。标准正交矩阵有一个很吸引人的性质：它的逆矩阵等于它的转置矩阵，所以：



通常来说，标准正交矩阵是非常值得使用的，因为它的逆矩阵可以很简单和高效的计算出来。

在特殊情况下，如果我们要围绕x，y，z轴旋转，我们可以得到下列矩阵：

---

---

2 仿射变换

---

2.1 齐次坐标系

在下一节中，我们将看到仿射变换其实是线性变换结合位移；位移不适用于向量，因为向量只表示方向和长度，其次坐标系中提供了一个计数方法可以点和向量的变化一致：

1、使用(x, y, z, 0)表示向量（w = 0可以保证向量在变化中不进行位移）；

2、使用(x, y, z, 0)表示点。

---

2.2 矩阵表示的定义

一个仿射变换是一个线性变化加一个位移变化：

a(u)=τ(u)+ba(u) = τ(u) + ba(u)=τ(u)+b

或者用矩阵表示：



如果我们使用w = 1来扩展到齐次坐标系，那么可以使用更简洁的写法：



这个4 x 4矩阵就是仿射变换的矩阵表示，如果是针对向量，不想做位移操作，只需要把第四行w设置为0即可。

---

2.3 位移

位移矩阵：



位移矩阵的逆矩阵：

---

2.4 仿射矩阵的缩放和旋转

---

2.5 仿射矩阵变换的几何解释

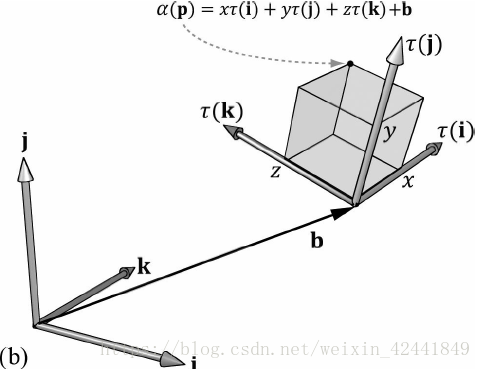
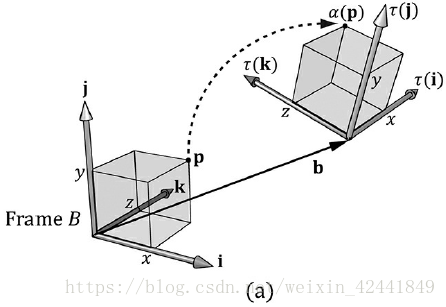
令τ是一个旋转变换，b是一个平移变换，那么这个变换就可以描述为一个仿射变换：

用其次坐标系（对于顶点w=1，对向量w=0）的矩阵表示为：

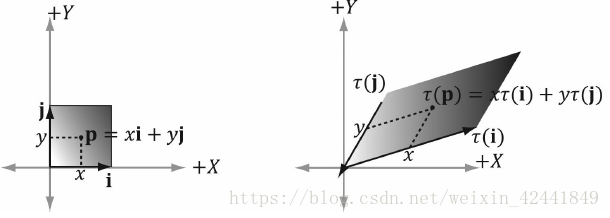
我们可以看到τ只是旋转了每一个标准分向量i，j和k；α(x, y, z) = xτ(i) + yτ(j) + zτ(k) + b，向量b只是平移了每一个顶点：

相同的思路也可以解释缩放变换：

---

---

3 变换的结合

假设S是一个缩放矩阵，R是一个旋转矩阵，T是一个平移矩阵；如果我们要对一个具有8个顶点的立方体做如何变换，最显而易见的方法是一步一步变换：

因为矩阵的乘法具有结合律，所以：



我们可以设C = SRT为一个同时封装了3个变换的矩阵。

---

---

4 坐标系变换

在3D计算机图形学中，我们需要使用到多个坐标系和坐标系之间的变换，对于顶点和向量的坐标系变幻是不同的。

---

4.1 向量

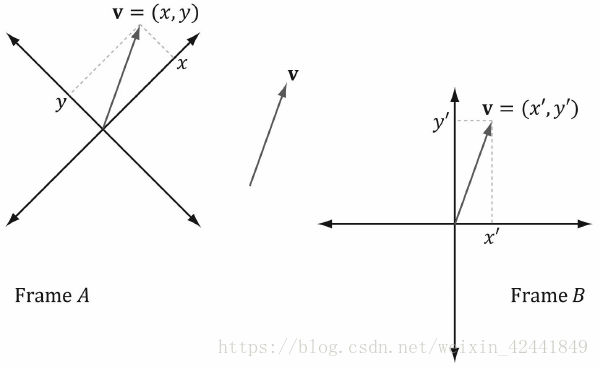
下图中，有两个坐标系A和B，与一个向量P。



很明显 p = xu + yv，其中u和v是坐标系A中，x和y方向上的单位向量；那么PBP_BPB​就可以解释为PB=xuB+yvBP_B = xu_B + yv_BPB​=xuB​+yvB​；所以，如果我们知道uB=(ux,uy)u_B = (u_x, u_y)uB​=(ux​,uy​)和vB=(vx,vy)v_B = (v_x, v_y)vB​=(vx​,vy​)，那么我们就可以计算出pB=(x′,y′)p_B = (x', y')pB​=(x′,y′)。

扩展到3D情况：

---

4.2 点

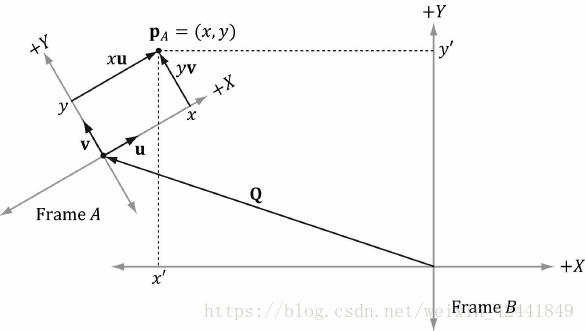
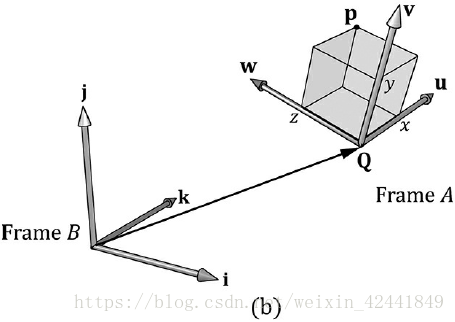
点的变换和向量有一点不同，点的位置很重要，如下图：



P点在坐标系A中可以表示为p = xu + yv + Q，那么在B坐标系中可以表示为PB=xuB+yvB+QBP_B = xu_B + yv_B + Q_BPB​=xuB​+yvB​+QB​；所以，如果我们知道uB=(ux,uy)u_B = (u_x, u_y)uB​=(ux​,uy​)、vB=(vx,vy)v_B = (v_x, v_y)vB​=(vx​,vy​)和QB=(Qx,Qy)Q_B = (Q_x, Q_y)QB​=(Qx​,Qy​)，那么我们就可以计算出pB=(x′,y′)p_B = (x', y')pB​=(x′,y′)。

扩展到3D的情况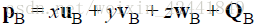：（其中Q是原点）

---

4.3 矩阵的表示

在齐次坐标系下：

那么矩阵表示如下：



我们称上述矩阵为一个坐标系变换矩阵，它将坐标系A变换到坐标系B。

---

4.4 坐标系变换矩阵的结合律

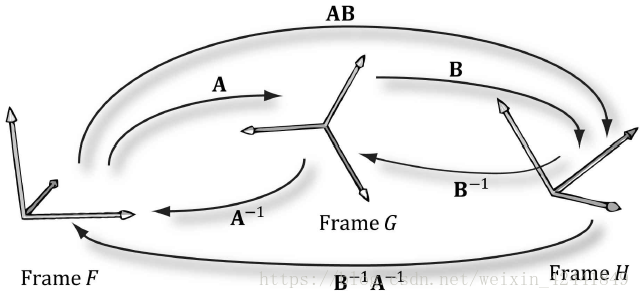
假设我们有3个坐标你F，G，H；矩阵A可以从F变换到G，矩阵B可以从G变换到H；我们希望将向量p从F变换到H，最显而易见的方法就是一步一步变换：

根据矩阵的乘法结合律：

在这种情况下，矩阵C= AB可以将p直接从F坐标系变换到H坐标系。（再次提醒，矩阵的乘法不支持交换律）

---

4.5 坐标系变换矩阵的逆矩阵

假设我们有一个在B坐标系的向量p，我们有从坐标系A变换到B的矩阵M，如果将P变换到坐标系A，乘以M的逆矩阵就可以了：

在本书中提到的坐标系变换映射都是可逆的，所以不需要担心是否存在逆矩阵。

---

---

5 变换矩阵 vs 坐标系变换矩阵

变换矩阵和坐标系变换矩阵是相同的，变化矩阵可以被解释为一个坐标系变换矩阵，反之亦然。

---

---

6 DIRECTX MATH 中的变换函数

在DIRECTX MATH中与变换函数相关的总结如下：

// Constructs a scaling matrix:
XMMATRIX XM_CALLCONV XMMatrixScaling(
float ScaleX,
float ScaleY,
float ScaleZ); // Scaling factors

// Constructs a scaling matrix from components in vector:
XMMATRIX XM_CALLCONV XMMatrixScalingFromVector(
FXMVECTOR Scale); // Scaling factors (sx, sy, sz)

// Constructs a x-axis rotation matrix Rx:
XMMATRIX XM_CALLCONV XMMatrixRotationX(
float Angle); // Clockwise angle θ to rotate

// Constructs a y-axis rotation matrix Ry:
XMMATRIX XM_CALLCONV XMMatrixRotationY(
float Angle); // Clockwise angle θ to rotate

// Constructs a z-axis rotation matrix Rz:
XMMATRIX XM_CALLCONV XMMatrixRotationZ(
float Angle); // Clockwise angle θ to rotate

// Constructs an arbitrary axis rotation matrix Rn:
XMMATRIX XM_CALLCONV XMMatrixRotationAxis(
FXMVECTOR Axis, // Axis n to rotate about
float Angle); // Clockwise angle θ to rotate

// Constructs a translation matrix:
XMMATRIX XM_CALLCONV XMMatrixTranslation(
float OffsetX,
float OffsetY,
float OffsetZ); // Translation factors

// Constructs a translation matrix from components in a vector:
XMMATRIX XM_CALLCONV XMMatrixTranslationFromVector(
FXMVECTOR Offset); // Translation factors (tx, ty, tz)

// Computes the vector-matrix product vM where vw = 1 for transforming points:
XMVECTOR XM_CALLCONV XMVector3TransformCoord(
FXMVECTOR V, // Input v
CXMMATRIX M); // Input M

// Computes the vector-matrix product vM where vw = 0 for transforming vectors:
XMVECTOR XM_CALLCONV XMVector3TransformNormal(
FXMVECTOR V, // Input v
CXMMATRIX M); // Input M

最后两个函数XMVector3TransformCoord和XMVector3TransformNormal，你不需要手动设置w = 0还是1，因为函数中会强制设置w的值。

---

---

7 本章总结

1. 基础的变换矩阵：旋转，缩放和平移矩阵公式如下：
   
   
2. 我们使用4x4矩阵表示变换；用1x4齐次坐标系来描述顶点和向量，其第四个值w，对于顶点为1，对于向量为0；
3. 一个矩阵如果其4行向量都是单位向量并且相互垂直，则该矩阵为正交矩阵；正交矩阵的逆矩阵和它的转置矩阵相等，所以它的逆矩阵计算起来很简单和高效，所有旋转矩阵都是正交矩阵；
4. 根据矩阵的乘法结合律，我们可以将多个变换矩阵合成为一个变化矩阵；
5. 令uBu_BuB​、vBv_BvB​、QBQ_BQB​和WBW_BWB​描述B坐标系下在A坐标系中的值，那么一个在A坐标系下的向量/顶点P，在B坐标系下的值就可以计算为：
   
   
6. 假设有3个坐标系F，G和H，并且A矩阵从F变换到G，B矩阵从G变换到H；我们可以得到C = AB矩阵从F变换到H；
7. 如果矩阵M可以从A坐标系变换到B坐标系，那么M的逆矩阵就可以从B坐标系变换到A坐标系；
8. 一个有效的变换可以被解释为坐标系变换，反之亦然。

---

---

8 练习题

1、定义如下变换：τ(x, y, z) = (x + y, x – 3, z)。τ是否为线性变换，如果是，找出它的矩阵表示：

2、定义如下变换：τ(x, y, z) = (3x + 4z, 2x – z, x + y + z)。τ是否为线性变换，如果是，找出它的矩阵表示：

3、假设τ是一个线性变换，进一步假设τ(1, 0, 0) = (3, 1, 2), τ(0, 1, 0) = (2, -1, 3), 和 τ(0, 0, 1) = (4, 0, 2)；找出τ(1, 1, 1)：

4、创建一个缩放矩阵，x轴方向放大2倍，y轴方向放大-3倍，Z轴保持不变：

5、创建一个旋转矩阵，围绕(1, 1, 1)旋转30度：

6、创建一个平移矩阵，x轴方向移动4，y轴方向不变，z轴方向移动-9：

7、创建一个矩阵，先缩放(2, -3, 0)，再平移(4, 0, -9)：

8、创建一个矩阵，先旋转(0, 45度, 0)，再平移(-2, 5, 1)：

9、重做例子3.2，这次缩放(1.5, 0.75, 1)，并且画图验证结果：

10、重做例子3.3，这次旋转（0，45度，0），并且画图验证结果：

11、重做例子3.4，这次平移(-5, -3, 4)，并且画图验证结果：

12、证明Rn(v)=cosθv+(1−cosθ)(n⋅v)n+sinθ(n×v)R_n(v) = cosθv + (1 − cosθ) (n·v)n + sinθ(n × v)Rn​(v)=cosθv+(1−cosθ)(n⋅v)n+sinθ(n×v)是线性变换，并且找到他的矩阵表示：

13、证明RyR_yRy​是标准正交的，为了更多扩展练习，读者也可以证明基本旋转矩阵也是标准正交的：

14、证明M是标准正交的，有且仅有当MT=M−1M^T = M^{-1}MT=M−1：

15、计算

这些计算移动顶点了吗，移动向量了吗？为什么没有移动向量在坐标系中的位置？

16、证明缩放矩阵的倒转就是它的逆矩阵，用矩阵的乘法表示为：SS−1=S−1S=ISS^{-1} = S^{-1}S = ISS−1=S−1S=I；同样的，证明平移矩阵：

17、假设我们有2个坐标系A和B，在A坐标系下的点p和力q；

令

创建从A坐标系映射到B坐标系的坐标系变换矩阵，并且计算在B坐标系下的p和q，并且画图验证结果：

18、