[SDOI2012] 任务安排 题解

有感而发，遂书。
其实和sze聊了很久，但他还是退役了。恐怕他是本届里学oi时间最长的一个人吧，从小学五年级开始。我也是因为他，才开始学oi的。他因为学校的压力，不得不放弃。或许是没什么天赋。学了4年也才一个pj2=,我也才学了半年多，就是省一。只是感叹罢了。在提高机房里，我是最小的。在普及机房里我是最大的。事实上，我又何尝不羡慕呢，也许，我再早一点，只要早半年，我就可以初三进省队。或许，这是对我挥霍初二一年时光的惩罚吧。

时光荏苒，你我不再是少年。

题意分析

我们看一下弱化版，再看下标准版

我们很简单的有一个dp的造作，事实上是可以过掉第一题的

定义 \(f_i\)表示完成\(1\)至\(i\)任务所需的最少花费。

所求 \(f_n\)即为所求

为了书写方便。我们做一个前缀和 定义 c,t就像题面所说的

dp转移方程
\[
f[i]=min_{0 \le j < i}\{ f[j]+s*(c[n]-c[j])+t[i]*(c[i]-c[j])\}
\]

轻轻一跃跳入坑中

我们这里用了一种想法，就是把后面任务的启动时间算到这一次，这样就不用统计他的记录分了几批任务的状态。

运用这个dp的转移是\(O(n^2)\)的，可以过掉第一题，但是第二题还差优化。

观察了第二题。由于是一维dp自然想到了决策的单调性。推了一下大概是满足的。于是我想到了斜率优化。。。。从此跳入了坑

我们把上面的dp方程做展开有：
\[
f[j]=(t[i]+s)*c[j]+(-t[i]*c[i]+f[i]-s*c[n])
\]
我们知道，如果能斜率优化dp方程必定能变为\(y=kx+b\) 的形式

其中y=只关于j的函数，x=只关于j的函数，k=只关于i的函数，b=只关于i的函数，k和x不严格单调递增。

我们的每个点就为\((c[j],f[j])\),此时，这不就是斜率优化的板子吗？开心的打上去。0pts滚粗

于是我们观察数据范围 \(|t_i| \le 2^8\)..有负的，所以我们不能维护单调队列。但是dp的决策是单调的！

那就再跳出来

那就用一个单调栈。

我们的单调队列维护了一个下图

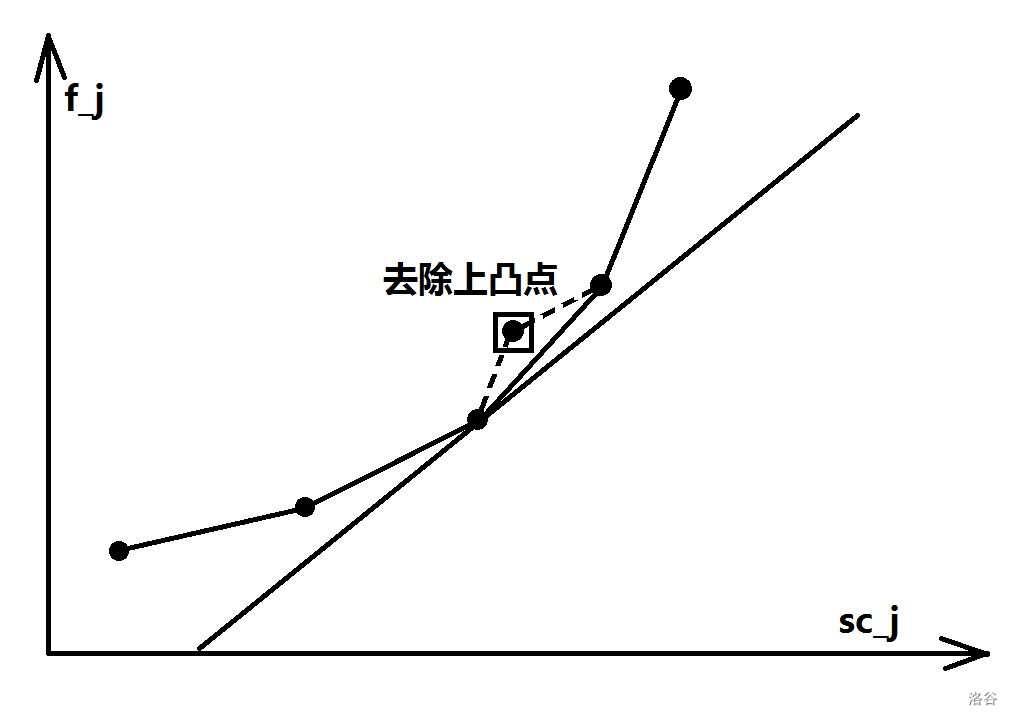
然而k不是单增的，显然的，上凸点依然不可能成为决策点。所以我们要维护的就是一个下凸包就如下图：

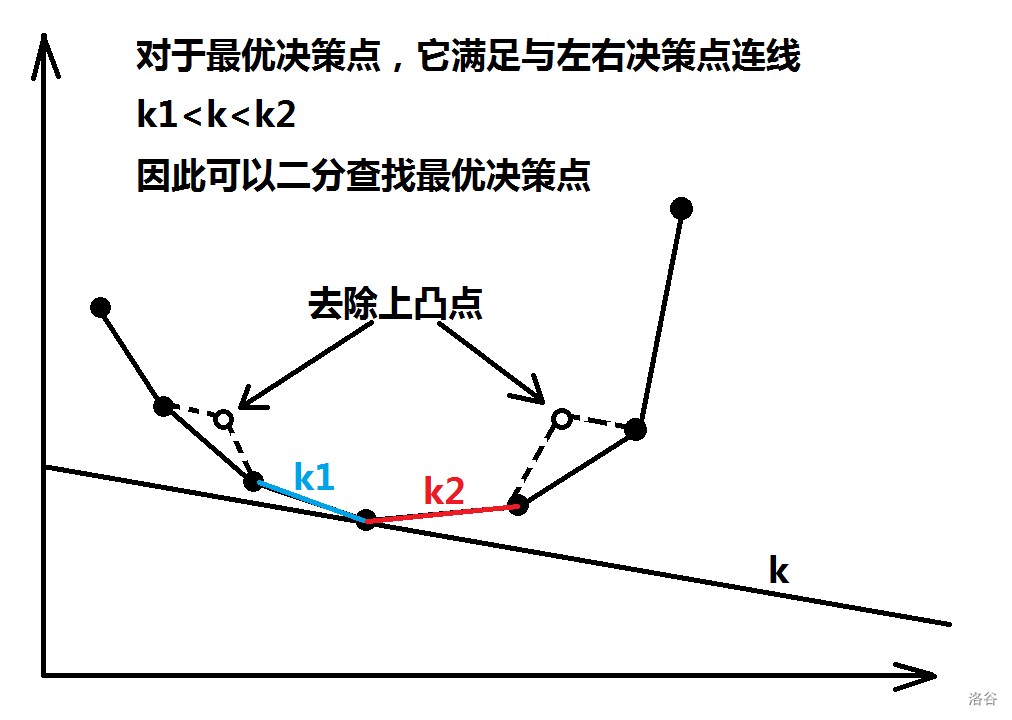
再找最优决策点是可以二分来找

可以用单调栈来维护

#include <iostream>
#include <cstdio>
#include <cstring>
#include <cmath>
#include <queue>
using namespace std;
typedef long long ll;
typedef double db;
const int Maxn=3*1e5+11;
ll n,s,c[Maxn],t[Maxn],q[Maxn],tail,head;
ll f[Maxn];
ll read(){
    ll x=0;
    bool f=0;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-') f=1;
        ch=getchar();
    }
    while(ch<='9'&&ch>='0'){
        x=(x<<1)+(x<<3)+(ch-'0');
        ch=getchar();
    }
    if(f) return -x;
    return x;
}
ll search(ll head,ll tail,ll k){
    if(head==tail) return q[head];
    ll ans;
    while(head<=tail){
        ll mid=(head+tail)>>1;
        if((f[q[mid+1]]-f[q[mid]])>(ll)k*(c[q[mid+1]]-c[q[mid]])){
            // 维护下凸壳去第一个 slope(mid,mid+1)>k，因为下凸壳k单增
            tail=mid-1;
            ans=mid;
        }
        else head=mid+1;
    }
    return q[ans];
}
int main(){
    freopen("SDOItask.in","r",stdin);
    n=read();s=read();
    for(int i=1;i<=n;i++) t[i]=t[i-1]+read(),c[i]=c[i-1]+read();
    tail=1;head=1;
    for(int i=1;i<=n;i++){
        ll p=search(head,tail,s+t[i]);
        f[i]=f[p]+t[i]*(c[i]-c[p])+s*(c[n]-c[p]);
        while(head<tail&&(f[i]-f[q[tail]])*(ll)(c[q[tail]]-c[q[tail-1]])<=(f[q[tail]]-f[q[tail-1]])*(ll)(c[i]-c[q[tail]])) tail--;
        q[++tail]=i;
    }
    printf("%lld",f[n]);
    return 0;
}

嵬

讲真的，我不会线段树。。。