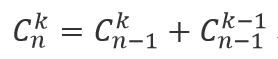HDU - 6333 Problem B. Harvest of Apples (莫队)
Count the number of ways to pick at most mm apples.
Input
The first line of the input contains an integer TT (1≤T≤105)(1≤T≤105) denoting the number of test cases.
Each test case consists of one line with two integers n,mn,m (1≤m≤n≤105)(1≤m≤n≤105).
Output
For each test case, print an integer representing the number of ways modulo 109+7109+7.Sample Input
2
5 2
1000 500
Sample Output
16
924129523 题意:
给定多个n,m,求C(n,m)
思路:
数据范围比较大,不能进行预处理。
我们可以采用莫队算法解决这个查询问题。
当n变大时,按此试展开,再和原式相比较,便可以得出转换公式。
n变小同理。
k的变化直接加减即可。
注意:变化过程中,可能使n>m,这个时候计算C的函数直接返回0就好了。
逆元要预处理,否则会T。
#include<iostream>
#include<algorithm>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<ctime>
#define fuck(x) cout<<#x<<" = "<<x<<endl;
#define debug(a,i) cout<<#a<<"["<<i<<"] = "<<a[i]<<endl;
#define ls (t<<1)
#define rs ((t<<1)+1)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = ;
const int maxm = ;
const int inf = 2.1e9;
const ll Inf = ;
const int mod = ;
const double eps = 1e-;
const double pi = acos(-); struct node{
int l,r;
int id;
}a[maxm];
ll anss[maxm];
int block; bool cmp(node a,node b){
return (a.l/block!=b.l/block)?a.l<b.l:a.r<b.r;
}
int vis[];
ll q_pow(ll a,ll b){
ll ans=;
while(b){
if(b&){ans*=a;ans%=mod;}
a*=a;
a%=mod;
b>>=;
}
return ans;
}
ll cal[maxn];
ll inv[maxn];
ll C(int n,int m){
if(n<||m<||m>n){return ;}
return cal[n]*inv[m]%mod*inv[n-m]%mod;
} int main()
{ cal[]=;inv[]=;
for(int i=;i<maxn;i++){
cal[i]=cal[i-]*i;
cal[i]%=mod;
inv[i]=q_pow(cal[i],mod-);
inv[i]%=mod;
} int m;
scanf("%d",&m);
int mx=;
for(int i=;i<=m;i++){
scanf("%d%d",&a[i].l,&a[i].r);
a[i].id=i;
mx=max(mx,a[i].l);
}
block=sqrt(mx);
sort(a+,a++m,cmp); ll L=,R=;
ll ans=;
for(int i=;i<=m;i++){
while(L>a[i].l){
ans+=C(L-,R);
ans%=mod;
ans*=q_pow(,mod-);
ans%=mod;
L--;
}
while(R<a[i].r){
R++;
ans+=C(L,R);
ans%=mod;
}
while(L<a[i].l){
ans*=;
ans%=mod;
ans-=C(L,R);
ans+=mod+mod;
ans%=mod;
L++;
}
while(R>a[i].r){
ans-=C(L,R);
ans+=mod+mod;
ans%=mod;
R--;
}
ans%=mod;
anss[a[i].id]=ans;
} for(int i=;i<=m;i++){
printf("%lld\n",anss[i]);
}
return ;
}
HDU - 6333 Problem B. Harvest of Apples (莫队)的更多相关文章
- HDU - 6333 Problem B. Harvest of Apples (莫队+组合数学)
题意:计算C(n,0)到C(n,m)的和,T(T<=1e5)组数据. 分析:预处理出阶乘和其逆元.但如果每次O(m)累加,那么会超时. 定义 S(n, m) = sigma(C(n,m)).有公 ...
- Problem B. Harvest of Apples 莫队求组合数前缀和
Problem Description There are n apples on a tree, numbered from 1 to n.Count the number of ways to p ...
- HDU-6333 Problem B. Harvest of Apples 莫队
HDU-6333 题意: 有n个不同的苹果,你最多可以拿m个,问有多少种取法,多组数据,组数和n,m都是1e5,所以打表也打不了. 思路: 这道题要用到组合数的性质,记S(n,m)为从n中最多取m个的 ...
- HDU 6333.Problem B. Harvest of Apples-组合数C(n,0)到C(n,m)求和-组合数学(逆元)+莫队 ((2018 Multi-University Training Contest 4 1002))
2018 Multi-University Training Contest 4 6333.Problem B. Harvest of Apples 题意很好懂,就是组合数求和. 官方题解: 我来叨叨 ...
- 2018 Multi-University Training Contest 4 Problem B. Harvest of Apples 【莫队+排列组合+逆元预处理技巧】
任意门:http://acm.hdu.edu.cn/showproblem.php?pid=6333 Problem B. Harvest of Apples Time Limit: 4000/200 ...
- hdu6333 Problem B. Harvest of Apples(组合数+莫队)
hdu6333 Problem B. Harvest of Apples 题目传送门 题意: 求(0,n)~(m,n)组合数之和 题解: C(n,m)=C(n-1,m-1)+C(n-1,m) 设 ...
- 【魔改】莫队算法+组合数公式 杭电多校赛4 Problem B. Harvest of Apples
http://acm.hdu.edu.cn/showproblem.php?pid=6333 莫队算法是一个离线区间分块瞎搞算法,只要满足:1.离线 2.可以O(1)从区间(L,R)更新到(L±1, ...
- Problem B. Harvest of Apples(杭电2018年多校+组合数+逆元+莫队)
题目链接:http://acm.hdu.edu.cn/showproblem.php?pid=6333 题目: 题意:求C(n,0)+C(n,1)+……+C(n,m)的值. 思路:由于t和n数值范围太 ...
- 热身训练1 Problem B. Harvest of Apples
http://acm.hdu.edu.cn/showproblem.php?pid=6333 题意: 求 C(0,n)+C(1,n)+...+C(m,n) 分析: 这道题,我们令s(m,n) = C( ...
随机推荐
- HTML5八大特性助力移动WebApp开发
http://www.cocoachina.com/webapp/20150906/13344.html WebApp的实现基础就是HMTL5+JS+CSS3,但是WebApp还是基于浏览器的微网站开 ...
- oracle Sql语句分类
dml语句:数据操作语句[insert,update,delete] ddl语句:数据定义语言[create table,drop table] dql语句:数据查询语句[select] dtl语句: ...
- C++返回值优化
返回值优化(Return Value Optimization,简称RVO)是一种编译器优化机制:当函数需要返回一个对象的时候,如果自己创建一个临时对象用于返回,那么这个临时对象会消耗一个构造函数(C ...
- C-链表实现,保存文件,评估-单项选择题系统课程设计---ShinePans
课程设计 单项选择题标准化考试系 所属专业:软件project软件三班 完毕人:潘尚 一.设计计划. 1.能够用菜单明白的指导用户操作. 2.操作完毕能够返回主菜单. 3.将输入的题目保存至C盘的 ...
- HDU-4807-Lunch Time(二分+费用流,思维)
这道题非常好,如果没有真正弄懂费用流算法的人,只会套模版的人是肯定做不出来的. 我们其实这样考虑,费用流真正的思想是吧费用作为长度,然后跑最短路,同时保证路上的流量不为0,也就是增广: 跑到终点后,回 ...
- 我钟爱的HTML5和CSS3在线工具【转】
我真的喜欢上了HTML5, CSS3, JavaScript编程,但是有一些代码还是需要一些辅助工具来做才行,例如,CSS3的Gradient渐变如果手写代码的话真的不爽,还有像animation动画 ...
- 容器安全拾遗 - Rootless Container初探
摘要: Docker和Kubernetes已经成为企业IT架构的基础设施,安全容器运行时越来越被关注.近期Docker 19.03中发布了一个重要的特性 “Rootless Container”,在提 ...
- 使用vux组件库常见报错($t)处理
错误一: [Vue warn]: Property or method "$t" is not defined on the instance but referenced dur ...
- H3C 分页显示
- oracle用>=替代>
如果DEPTNO上有一个索引, 高效: SELECT * FROM EMP WHERE DEPTNO >=4 低效: SELECT * FROM EMP WHERE DEPTNO >3 两 ...