七.RBM受限玻尔兹曼机

1、受限玻尔兹曼机

　玻尔兹曼机是一大类的神经网络模型，但是在实际应用中使用最多的则是受限玻尔兹曼机（RBM）。

　　受限玻尔兹曼机（RBM）是一个随机神经网络（即当网络的神经元节点被激活时会有随机行为，随机取值）。它包含一层可视层和一层隐藏层。在同一层的神经元之间是相互独立的，而在不同的网络层之间的神经元是相互连接的（双向连接）。在网络进行训练以及使用时信息会在两个方向上流动，而且两个方向上的权值是相同的。但是偏置值是不同的（偏置值的个数是和神经元的个数相同的），受限玻尔兹曼机的结构如下

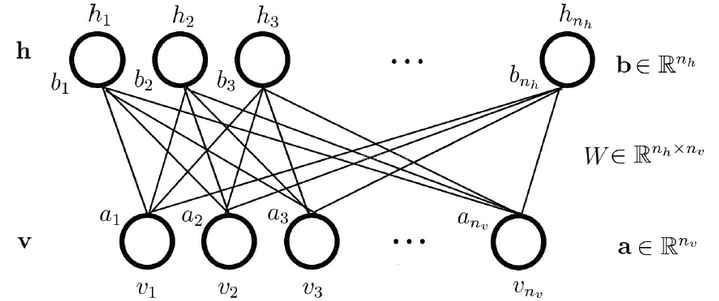
　　上面一层神经元组成隐藏层(hidden layer), 用h向量隐藏层神经元的值。下面一层的神经元组成可见层(visible layer),用v向量表示可见层神经元的值。连接权重可以用矩阵W表示。和DNN的区别是，RBM不区分前向和反向，可见层的状态可以作用于隐藏层，而隐藏层的状态也可以作用于可见层。隐藏层的偏倚系数是向量b,而可见层的偏倚系数是向量a。

　　常用的RBM一般是二值的，即不管是隐藏层还是可见层，它们的神经元的取值只为0或者1。

　　RBM模型结构的结构：主要是权重矩阵W, 偏倚系数向量a和b，隐藏层神经元状态向量h和可见层神经元状态向量v。

2、能量函数和概率分布

　　RBM是基于基于能量的概率分布模型。分为两个部分：第一部分是能量函数，第二部分是基于能量函数的概率分布函数。对于给定的状态向量h和v，则RBM当前的能量函数可以表示为：

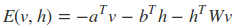
　　其中a，b是偏倚系数，而W是权重矩阵。有了能量函数，v,h的联合概率分布为：

　　其中Z是被称为配分函数的归一化常数（对于概率输出一般都要做归一化）：

　　由于配分函数Z的难以处理，所以必须使用最大似然梯度来近似。首先从联合分布中导出条件分布：

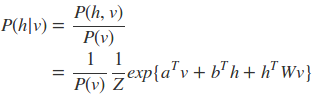
　　为了推导方便将无关值归于Z’中：

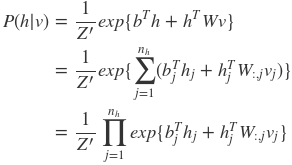
　　可以容易的得到在给定可视层v的基础上，隐层第j个节点为1或者为0的概率为：

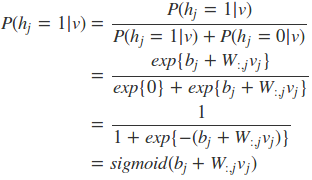
　　可以看到就是相当于使用了sigmoid激活函数，现在可以写出关于隐藏层的完全条件分布：

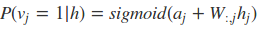
　　有了激活函数，我们就可以从可见层和参数推导出隐藏层的神经元的取值概率了。对于0,1取值的情况，则大于0.5即取值为1。从隐藏层和参数推导出可见的神经元的取值方法也是一样的。

3、RBM损失函数　

　　RBM模型的关键就是求出我们模型中的参数W,a,b。首先我们得写出损失函数，RBM一般采用对数损失函数，即期望最小化下式：

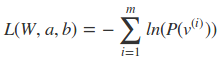
　　然后求偏导可得：

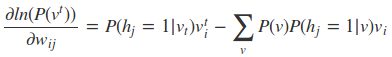
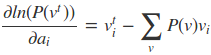
　　虽然说梯度下降从理论上可以用来优化RBM模型，但实际中是很难求得P(v)的概率分布的（P(v)表示可见层节点的联合概率）。计算复杂度非常大，因此采用一些随机采样的方法来得到近似的解。看这三个梯度的第二项实际上都是求期望，而我们知道，样本的均值是随机变量期望的无偏估计。因此一般都是基于对比散度方法来求解。

4、对比散度算法（CD）

　　CD算法大概思路是这样的，从样本集任意一个样本v⁰开始，经过k次Gibbs采样（实际中k=1往往就足够了），即每一步是：

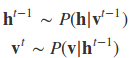
　　得到样本v^k，然后对应于上一篇三个单样本的梯度，用v^k去近似：

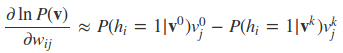
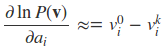
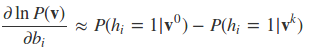
　　上述近似的含义是说，用一个采样出来的样本来近似期望的计算。下面给出CD-k的算法执行流程。

　　具体RBM算法的流程：

5、深度玻尔兹曼机（DBM）

　　加深RBM的层数后，就变成了DBM，结构图如下：

　　此时的能量函数变为：

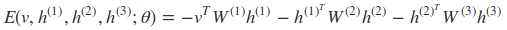
　　联合概率变成：

　　其实DBM也可以看做是一个RBM，比如对上图稍微加以变换就可以看做是一个RBM。

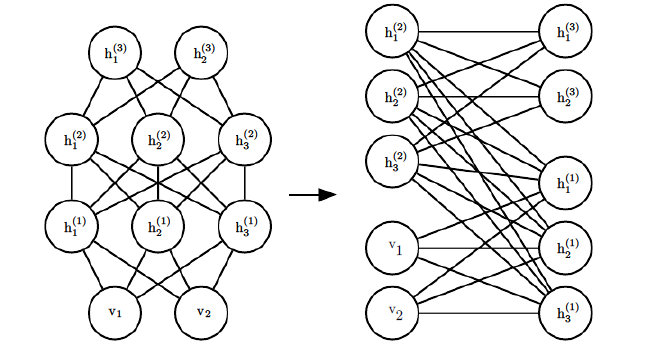
　　将可见层和偶数隐藏层放在一边，将奇数隐藏层放在另一边，我们就得到了RBM，和RBM的细微区别只是现在的RBM并不是全连接的，其实也可以看做部分权重为0的全连接RBM。RBM的算法思想可以在DBM上使用。只是此时我们的模型参数更加的多，而且迭代求解参数也更加复杂了。