「学习笔记」 FHQ Treap
FHQ Treap
FHQ Treap (%%%发明者范浩强年年NOI金牌)是一种神奇的数据结构,也叫非旋Treap,它不像Treap zig zag搞不清楚(所以叫非旋嘛),也不像Splay完全看不懂,而且它能完成Treap与Splay能完成的所有事,代码短,理解也容易。
基本操作
FHQ Treap和Treap很像,都是给每个节点一个随机的权值,使它满足堆的性质。建议先了解Treap(没必要实现,懂得原理即可)。不过,如果有两个节点值相同,FHQ Treap不会用一个数组cnt记录个数,而是直接再开一个节点。
FHQ的基本操作只有两个:Split与Merge。
Split表示把一棵树分成两棵,Merge表示把一棵树合并成一棵。
变量&函数约定
int L[MAXN], R[MAXN], sz[MAXN], rk[MAXN], val[MAXN], tot;
int root;
int New( int v ){ return val[++tot] = v, rk[tot] = rand(), L[tot] = R[tot] = 0, sz[tot] = 1, tot; }
#define Updata(x) sz[x] = sz[L[x]] + sz[R[x]] + 1
没写成结构体,没写成指针。
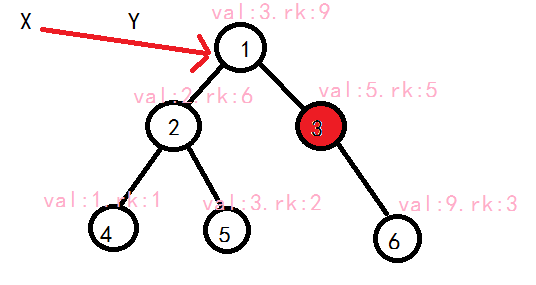
\(L[i]\)表示\(i\)的左儿子,\(R[i]\)表示\(i\)的右儿子,\(sz[i]\)表示以\(i\)为根的子树包含的节点数,\(rk[i]\)表示为了保持平衡随机赋予的权值,\(val[i]\)表示该节点保存的值,\(tot\)表示节点数,\(root\)表示当前的根节点。
\(New(v)\)表示新建一个值为\(v\)的节点(可以看成一棵只有一个节点平衡树)
\(Updata(x)\)表示更新节点\(x\)的\(sz\)
提醒:这里“值”与“权值”是不一样的,“值”表示节点保存的值,“权值“仅仅用于维持平衡,注意区分
Split
怎么分割呢?
常见的分割方法有两种,一种是按值分,一种是按排名分(实现差不多,这里只讲按值分)。
先来看看定义。
void Split( int c, int k, int &x, int &y );
c表示当前要分割的树的根节点,并且把值\(\le k\)的节点分割出来,构成一棵树,把\(x\)赋为根节点,其他节点另外构成一棵树,把\(y\)赋为其根节点。\(x\)、\(y\)用引用(&)更方便处理。
对于当前的树,如果根节点\(c\)的值\(\le k\),\(c\)的左子树也全部\(\le k\),所以我们可以把\(x\)赋为\(c\),保留左子树,将右子树\(\le k\)的部分分割出来作为\(x\)的右子树。剩下的部分自然也就是在\(> k\)的部分。\(>k\)的情况同理。具体我们用递归实现。
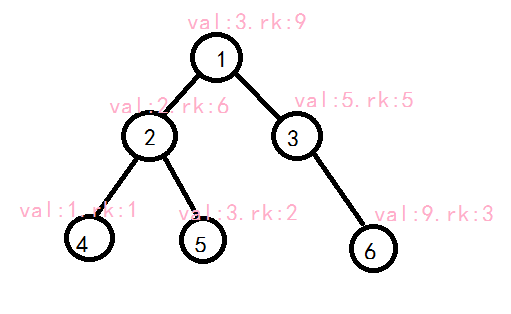
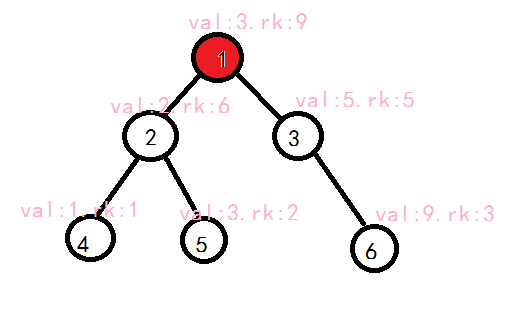
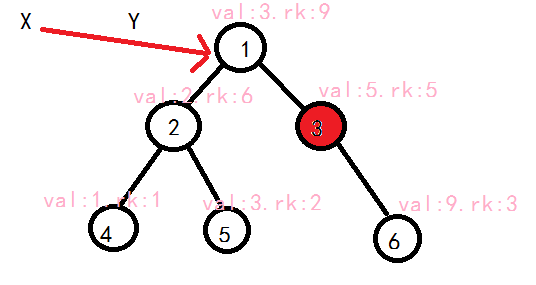
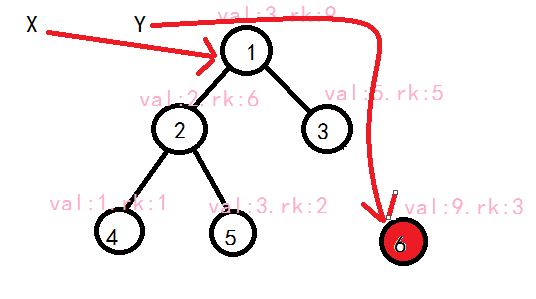
void Split( int c, int k, int &x, int &y ){
if ( c == 0 ){ x = y = 0; return; }//如果当前处理的树为空,分出的两个子树当然也为空,所以直接赋值返回。
if ( val[c] <= k ) x = c, Split( R[c], k, R[x], y );//如果根节点值小于等于k,把x赋为c,继续处理右子树,并把小于等于k的部分分到x的右子树,其他分到y
else y = c, Split( L[c], k, x, L[y] );
Updata(c);//别忘了更新sz
}
Merge
上面分割的操作不会改变堆的性质与二叉查找树的性质,但是在合并的时候要注意保持堆的性质。
void Merge( int &c, int x, int y );
表示把以\(x\)和\(y\)为根节点的树合并,将\(c\)赋为根节点。
注意:上面分割时x的所有节点的值都小于y的,合并时也要注意x的所有节点小于等于y,否则会出错
由于\(x\)与\(y\)的权值在两颗树中是最大的,所以合并后的树根节点不是\(x\)就是\(y\)。所以比较\(x\)与\(y\)的权值就可以判断谁为根节点。
假设以\(x\)为根。因为保证\(x\)的所有节点的值都小于等于\(y\)的,所以\(y\)肯定会合并在\(x\)的右子树。所以,我们不用动\(x\)的左子树,合并\(x\)的右子树与\(y\)作为\(x\)的右子树。\(y\)为根时同理。这样,就巧妙完成了同时维护堆的性质与二叉查找树的性质。
我们还是用递归。
void Merge( int &c, int x, int y ){
if ( !x || !y ){ c = x | y; return; }
if ( rk[x] >= rk[y] ) c = x, Merge( R[x], R[c], y );
else c = y, Merge( L[y], x, L[c] );
Updata(c);
}
我刚开始也理解不了这两种操作。主要瓶颈在难以想象。其实可以看做只处理当前的,未处理的留到下一步,反正操作方法都一样。
剩下的都可以用这两种操作实现。
插入操作
直接把它分成\(\le v\)的树和\(> v\)的树,将新建的节点与\(\le v\)的树合并,再与\(>y\)树合并即可。
//opt 1
void Ins( int v ){
int x, y, z(New(v));
Split( root, v, x, y );
Merge( x, x, z );
Merge( root, x, y );
}
删除操作
分成\(\le k\)和\(> k\)两颗树,再分成\(<k\)、\(=k\)、\(> k\)三棵树,将\(=k\)左右子树合并,相当于删去\(=k\)的一个节点,然后将三棵树重新合并即可。
// opt 2
void Del( int v ){
int x, y, z;
Split( root, v, x, y );
Split( x, v - 1, x, z );
Merge( z, L[z], R[z] );
Merge( x, x, z );
Merge( root, x, y );
}
查询排名
其实可以用while循环,,,但是,,,我,,,懒,,,所,,,以,,,直,,,接,,,,,,,
//opt 3
int GetRankByVal( int v ){
int x, y, t;
Split( root, v - 1, x, y );
t = sz[x];
Merge( root, x, y );
return t + 1;
}
查询值
这真的不能用Split和Merge偷懒了,,,所以乖乖写个while吧~
技术含量不高,自行理解。
//opt 4
int GetValByRank( int rk ){
int c(root);
while( c ){
if ( sz[L[c]] + 1 == rk ) return val[c];
else if ( sz[L[c]] >= rk ) c = L[c];
else rk -= 1 + sz[L[c]], c = R[c];
}
return -1;//题目没要求。。。只是为了自己查错
}
查询前缀
分成两颗树\(<v\)与\(\ge v\),在\(<v\)树中找最大值即可。
//opt 5
int GetPre( int v ){
int x, y, z;
Split( root, v - 1, x, y );
z = x;
while( R[z] ) z = R[z];
Merge( root, x, y );
return val[z];
}
查询后缀
与查询前缀同理。
//opt 6
int GetNxt( int v ){
int x, y, z;
Split( root, v, x, y );
z = y;
while( L[z] ) z = L[z];
Merge( root, x, y );
return val[z];
}
完整代码
#include<bits/stdc++.h>
using namespace std;
#define MAXN 100005
int L[MAXN], R[MAXN], sz[MAXN], rk[MAXN], val[MAXN], tot;
int root;
int New( int v ){ return val[++tot] = v, rk[tot] = rand(), L[tot] = R[tot] = 0, sz[tot] = 1, tot; }
#define Updata(x) sz[x] = sz[L[x]] + sz[R[x]] + 1
void Split( int c, int k, int &x, int &y ){
if ( c == 0 ){ x = y = 0; return; }
if ( val[c] <= k ) x = c, Split( R[c], k, R[x], y );
else y = c, Split( L[c], k, x, L[y] );
Updata(c);
}
void Merge( int &c, int x, int y ){
if ( !x || !y ){ c = x | y; return; }
if ( rk[x] >= rk[y] ) c = x, Merge( R[x], R[c], y );
else c = y, Merge( L[y], x, L[c] );
Updata(c);
}
//opt 1
void Ins( int v ){
int x, y, z(New(v));
Split( root, v, x, y );
Merge( x, x, z );
Merge( root, x, y );
}
// opt 2
void Del( int v ){
int x, y, z;
Split( root, v, x, y );
Split( x, v - 1, x, z );
Merge( z, L[z], R[z] );
Merge( x, x, z );
Merge( root, x, y );
}
//opt 3
int GetRankByVal( int v ){
int x, y, t;
Split( root, v - 1, x, y );
t = sz[x];
Merge( root, x, y );
return t + 1;
}
//opt 4
int GetValByRank( int rk ){
int c(root);
while( c ){
if ( sz[L[c]] + 1 == rk ) return val[c];
else if ( sz[L[c]] >= rk ) c = L[c];
else rk -= 1 + sz[L[c]], c = R[c];
}
return -1;
}
//opt 5
int GetPre( int v ){
int x, y, z;
Split( root, v - 1, x, y );
z = x;
while( R[z] ) z = R[z];
Merge( root, x, y );
return val[z];
}
//opt 6
int GetNxt( int v ){
int x, y, z;
Split( root, v, x, y );
z = y;
while( L[z] ) z = L[z];
Merge( root, x, y );
return val[z];
}
int T;
int main(){
srand(time(0));//随机数种子别忘了
root = New(INT_MAX);//虚节点,避免一个节点都没有不方便合并。注意要用一个很大的数,查询排名时就不用-1
scanf( "%d", &T );
while( T-- ){
int opt, x;
scanf( "%d%d", &opt, &x );
switch( opt ){
case 1: Ins(x); break;
case 2: Del(x); break;
case 3: printf( "%d\n", GetRankByVal(x) ); break;
case 4: printf( "%d\n", GetValByRank(x) ); break;
case 5: printf( "%d\n", GetPre(x) ); break;
case 6: printf( "%d\n", GetNxt(x) ); break;
}
}
return 0;
}
FHQ Treap还可以资瓷可持久化~比Treap、Splay好用多啦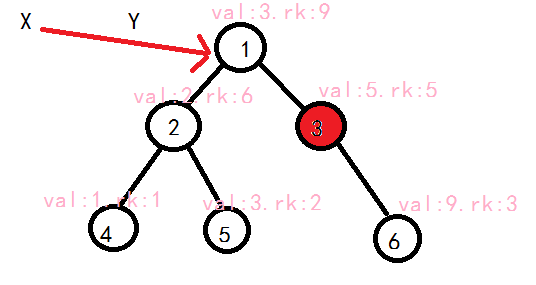
「学习笔记」 FHQ Treap的更多相关文章
- 「学习笔记」Treap
「学习笔记」Treap 前言 什么是 Treap ? 二叉搜索树 (Binary Search Tree/Binary Sort Tree/BST) 基础定义 查找元素 插入元素 删除元素 查找后继 ...
- 「学习笔记」Min25筛
「学习笔记」Min25筛 前言 周指导今天模拟赛五分钟秒第一题,十分钟说第二题是 \(\text{Min25}\) 筛板子题,要不是第三题出题人数据范围给错了,周指导十五分钟就 \(\text{AK ...
- 「学习笔记」FFT 之优化——NTT
目录 「学习笔记」FFT 之优化--NTT 前言 引入 快速数论变换--NTT 一些引申问题及解决方法 三模数 NTT 拆系数 FFT (MTT) 「学习笔记」FFT 之优化--NTT 前言 \(NT ...
- 「学习笔记」FFT 快速傅里叶变换
目录 「学习笔记」FFT 快速傅里叶变换 啥是 FFT 呀?它可以干什么? 必备芝士 点值表示 复数 傅立叶正变换 傅里叶逆变换 FFT 的代码实现 还会有的 NTT 和三模数 NTT... 「学习笔 ...
- 「学习笔记」字符串基础:Hash,KMP与Trie
「学习笔记」字符串基础:Hash,KMP与Trie 点击查看目录 目录 「学习笔记」字符串基础:Hash,KMP与Trie Hash 算法 代码 KMP 算法 前置知识:\(\text{Border} ...
- 「学习笔记」wqs二分/dp凸优化
[学习笔记]wqs二分/DP凸优化 从一个经典问题谈起: 有一个长度为 \(n\) 的序列 \(a\),要求找出恰好 \(k\) 个不相交的连续子序列,使得这 \(k\) 个序列的和最大 \(1 \l ...
- 「学习笔记」珂朵莉树 ODT
珂朵莉树,也叫ODT(Old Driver Tree 老司机树) 从前有一天,珂朵莉出现了... 然后有一天,珂朵莉树出现了... 看看图片的地址 Codeforces可还行) 没错,珂朵莉树来自Co ...
- 「学习笔记」ST表
问题引入 先让我们看一个简单的问题,有N个元素,Q次操作,每次操作需要求出一段区间内的最大/小值. 这就是著名的RMQ问题. RMQ问题的解法有很多,如线段树.单调队列(某些情况下).ST表等.这里主 ...
- 「学习笔记」递推 & 递归
引入 假设我们想计算 \(f(x) = x!\).除了简单的 for 循环,我们也可以使用递归. 递归是什么意思呢?我们可以把 \(f(x)\) 用 \(f(x - 1)\) 表示,即 \(f(x) ...
随机推荐
- @loj - 2288@「THUWC 2017」大葱的神力
目录 @description@ @solution@ @data - 1@ @data - 2@ @data - 3@ @data - 4@ @data - 5@ @data - 6@ @data ...
- 如何使用jmeter调用soap协议
- 2015,2016 Open Source Yearbook
https://opensource.com/yearbook/2015 The 2015 Open Source Yearbook is a community-contributed collec ...
- em&rem
PX特点 1. IE无法调整那些使用px作为单位的字体大小: 2. 国外的大部分网站能够调整的原因在于其使用了em或rem作为字体单位: 3. Firefox能够调整px和em,rem px像素(Pi ...
- 只要是使用函数file_get_contents访问 https 的网站都要开启
使用file_get_contents();报错failed to open stream: Unable to find the socket transport "ssl" - ...
- Oracle的dual是什么东西啊
原文:https://zhidao.baidu.com/question/170487574.html?fr=iks&word=dual&ie=gbk Oracle的dual是什么东西 ...
- 用winrar和zip命令拷贝目录结构
linux系统下使用zip命令 zip -r source.zip source -x *.php -x *.html # 压缩source目录,排除里面的php和html文件 windows系统下使 ...
- poj 3278(hdu 2717) Catch That Cow(bfs)
Catch That Cow Time Limit: 5000/2000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)To ...
- 2019-9-9-dotnet-获取本机-IP-地址方法
title author date CreateTime categories dotnet 获取本机 IP 地址方法 lindexi 2019-09-09 15:56:33 +0800 2019-0 ...
- [转]Jquery属性选择器(同时匹配多个条件,与或非)(附样例)
1. 前言 为了处理除了两项不符合条件外的选择,需要用到jquery选择器的多个条件匹配来处理,然后整理了一下相关的与或非的条件及其组合. 作为笔记记录. 2. 代码 1 2 3 4 5 6 7 8 ...
