Good Bye 2019（前五题题解）

这套也是后来补得。

我太菜了，第三题就卡着了。想了好久才做出来，要是参加了绝对掉分。

D题是人生中做完的第一道交互题，不容易。

比赛传送门

A.Card Game

题目大意：一共有n张互不相同的牌，玩家1有k1张牌，玩家2有k2张牌。两个人每次都会拿出一张牌，牌号大的人会得到这张牌，直到一方没牌。问第一个人能否会获胜。

这就是我们从小玩的比大小游戏。

在广大劳动人民的实践后得出来结论是有最大的牌的人获胜。

代码如下：

 #include <iostream>

 #include <cstdio>

 #include <algorithm>

 #include <cstring>

 #include <vector>

 #define rep(x, l, r) for(int x = l; x <= r; x++)

 #define repd(x, r, l) for(int x = r; x >= l; x--)

 #define clr(x, y) memset(x, y, sizeof(x))

 #define all(x) x.begin(), x.end()

 #define pb push_back

 #define mp make_pair

 #define MAXN

 #define fi first

 #define se second

 #define SZ(x) ((int)x.size())

 using namespace std;

 typedef long long ll;

 typedef vector<int> vi;

 typedef pair<int, int> pii;

 const int INF =  << ;

 const int p = ;

 int lowbit(int x){ return x & (-x);}

 int fast_power(int a, int b){ int x; for(x = ; b; b >>= ){ if(b & ) x = 1ll * x * a % p; a = 1ll * a * a % p;} return x % p;}

 int main(){

     int t;

     scanf("%d", &t);

     rep(times, , t){

         int n, k1, k2;

         scanf("%d%d%d", &n, &k1, &k2);

         int maxx1 = , maxx2 = ;

         rep(i, , k1){

             int x;

             scanf("%d", &x);

             maxx1 = max(maxx1, x);

         }

         rep(i, , k2){

             int x;

             scanf("%d", &x);

             maxx2 = max(maxx2, x);

         }

         if(maxx1 > maxx2) puts("YES");

         else puts("NO");

     }

     return ;

 }

-A

B.Interesting Subarray

题目大意：有一个数列a，让你找任意一个子段满足子段的最大值减最小值大于等于子段长度。

感觉这套的B题也比之前的难了点，看着屏幕愣了半天，可能最近脑子不对劲。

如果子段(l，r)满足条件，那么必定存在i，j满足a[i] - i < a[j] - j ，或者a[i] + i > a[j] + j。

那么只需记录下在所有的i，j( i <= j )，最小的a[i] - i和最大的a[i] + i，如果满足上面的条件就输出这一对。

代码如下:

 #include <iostream>

 #include <cstdio>

 #include <algorithm>

 #include <cstring>

 #include <vector>

 #define rep(x, l, r) for(int x = l; x <= r; x++)

 #define repd(x, r, l) for(int x = r; x >= l; x--)

 #define clr(x, y) memset(x, y, sizeof(x))

 #define all(x) x.begin(), x.end()

 #define pb push_back

 #define mp make_pair

 #define MAXN 200005

 #define fi first

 #define se second

 #define SZ(x) ((int)x.size())

 using namespace std;

 typedef long long ll;

 typedef vector<int> vi;

 typedef pair<int, int> pii;

 const int INF =  << ;

 const int p = ;

 int lowbit(int x){ return x & (-x);}

 int fast_power(int a, int b){ int x; for(x = ; b; b >>= ){ if(b & ) x = 1ll * x * a % p; a = 1ll * a * a % p;} return x % p;}

 int a[MAXN];

 int main(){

     int t;

     scanf("%d", &t);

     rep(times, , t){

         int n;

         scanf("%d", &n);

         rep(i, , n) scanf("%d", &a[i]);

         int s = INF, id = , ans = ;

         rep(i, , n){

             if(s < a[i] - i){

                 printf("YES\n%d %d\n", id, i);

                 ans = ;

                 break;

             }

             if(a[i] - i < s){

                 s = a[i] - i;

                 id = i;

             }

         }

         if(!ans){

             s = , id = ;

             rep(i, , n){

                 if(s > a[i] + i){

                     printf("YES\n%d %d\n", id, i);

                     ans = ;

                     break;

                 }

                 if(a[i] + i > s){

                     s = a[i] + i;

                     id = i;

                 }

             }

         }

         if(!ans) puts("NO");

     }

     return ;

 }

-B

C.Make Good

题目大意：给你一串数字，让你在其中插入最多3个数字，使得这些数字的总和等于异或的2倍，只要给出任何一种方案即可。

首先这串数字是和我们没关系了，我们需要的只是它们的异或以及和。

很显然，必定存在一种方案只放一个数字就能成立（不要问我为什么，程序员不需要证明）。

然后么将异或的乘个二，按照二进制来计算。

对于每一位，要是该位的为1，会对和产生1的贡献，对异或产生2的贡献，那么对于一个二进制位，要是这两个数不同，插入的数该位一定为1。

感觉解释的有点模糊……那就来个样例解释一下。

以下以[1,2,3,7]为例：

和：13 二进制：01101

异或：7 二进制：00111

异或的先乘个2也就是右移一位，为01110

0110 | 1

0111 | 0

两位置不同，答案该位为1，即加上1 << 0，变成1

和变成01110，异或变成01100，最后一位已经相同了，舍掉

011 | 1

011 | 0

不同，答案变成3，两数分别变成1000和0100，同样舍最后一位

10 | 0

01 | 0                    相同

1 | 0

0 | 1                      不同，答案变成11

| 1

| 1                         相同

插入后数列为 1， 2， 3， 7 ， 11符合条件

具体代码实现：

 #include <iostream>

 #include <cstdio>

 #include <algorithm>

 #include <cstring>

 #include <vector>

 #define rep(x, l, r) for(int x = l; x <= r; x++)

 #define repd(x, r, l) for(int x = r; x >= l; x--)

 #define clr(x, y) memset(x, y, sizeof(x))

 #define all(x) x.begin(), x.end()

 #define pb push_back

 #define mp make_pair

 #define MAXN

 #define fi first

 #define se second

 #define SZ(x) ((int)x.size())

 using namespace std;

 typedef long long ll;

 typedef vector<int> vi;

 typedef pair<int, int> pii;

 const int INF =  << ;

 const int p = ;

 int lowbit(int x){ return x & (-x);}

 int fast_power(int a, int b){ int x; for(x = ; b; b >>= ){ if(b & ) x = 1ll * x * a % p; a = 1ll * a * a % p;} return x % p;}

 int main(){

     int t;

     scanf("%d", &t);

     rep(times, , t){

         int n;

         scanf("%d", &n);

         ll s1 = , s2 = ;

         rep(i, , n){

             ll x;

             scanf("%lld", &x);

             s1 += x;

             s2 ^= x;

         }

         s2 <<= ;

         ll ans = ;

         for(int i = ; s1 != s2; i++){

             if((s1 & ) ^ (s2 & )){

                 s1 += ;

                 s2 ^= ;

                 ans += 1ll << i;

             }

             s1 >>= ;

             s2 >>= ;

         }

         printf("1\n%lld\n", ans);

     }

     return ;

 }

-D

D.Strange Device

题目大意：有一个长为n数列a，值已确定，但是你不知道。现在有个设备，你可以输入长为k的上升序列p₁,p₂,…,p_k，进行询问，它会回答a_p1，a_p2,...,a_pk中第m小的数在原数列的坐标和这个数的值。现在给你n和k，让你在最多询问n次后回答m的大小。

作为以往交互题直接跳的人，这题拿到一脸懵，后来还是看题解才有的思路。

我们只需要询问k+1次，第i次询问序列为{ x | 1 <= x <= k + 1, x <> i }

假设n = 4， k = 3，询问分别为

2 3 4

1 3 4

1 2 4

1 2 3

这样问有一个好处，第i次询问，若是i <= m，那么返回的必然是[a₁..a_{k +1}]中第m + 1小的数，否则返回的数必然是第m小的数。

那么在k+1次询问后，m+1小的数恰好返回了m次，于是我们答案就是返回的较大的一个数的次数。

代码如下：

 #include <iostream>

 #include <cstdio>

 #include <algorithm>

 #include <cstring>

 #include <vector>

 #include <map>

 #define rep(x, l, r) for(int x = l; x <= r; x++)

 #define repd(x, r, l) for(int x = r; x >= l; x--)

 #define clr(x, y) memset(x, y, sizeof(x))

 #define all(x) x.begin(), x.end()

 #define pb push_back

 #define mp make_pair

 #define MAXN

 #define fi first

 #define se second

 #define SZ(x) ((int)x.size())

 using namespace std;

 typedef long long ll;

 typedef vector<int> vi;

 typedef pair<int, int> pii;

 const int INF =  << ;

 const int p = ;

 int lowbit(int x){ return x & (-x);}

 int fast_power(int a, int b){ int x; for(x = ; b; b >>= ){ if(b & ) x = 1ll * x * a % p; a = 1ll * a * a % p;} return x % p;}

 map<int, int> f;

 int main(){

     int n, k;

     scanf("%d%d", &n, &k);

     int maxx = ;

     rep(i, , k + ){

         putchar('?');

         rep(j, , k + ){

             if(i == j) continue;

             printf(" %d", j);

         }

         puts("");

         fflush(stdout);

         int x, y;

         scanf("%d%d", &x, &y);

         f[y]++;

         maxx = max(maxx, y);

     }

     printf("! %d\n", f[maxx]);

     return ;

 }

-D

E.Divide Points

题目大意：给你n个点和它们的坐标，现在给它们两两连上边，如果在同一组为黄色，不同组为蓝色。现在让你给出任意一种分组方案，使得所有长度相同的边颜色相同。

相信大家看到这题目想的都是二分图啊，并查集啊……但我不一样，我想的是：这题目能做嘛……

大佬的做法真是高超，先放上题解里截来的图。

主要思路就是奇偶分类。

我们将点按照横纵坐标的奇偶性，分成4个集合。

其中点上的0,1表示坐标的奇偶性，边上的0,1表示长度平方的奇偶性。

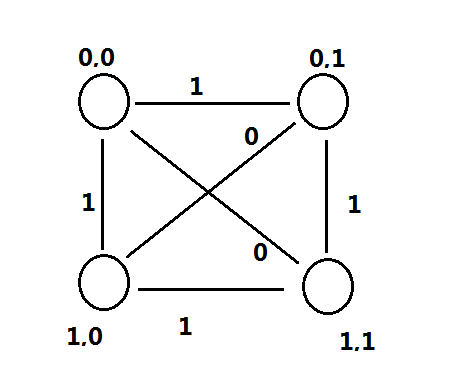
不难得出以上不同集合的点的关系，另外同一集合中的边当然也为0。

那么我们只要将(0,0)和(1,1)放入一组，(0,1)和(1,0)放入另一组，那么偶边（即长度平方为偶数的边）必定是同一组的两点，奇边必定是不同组的两点。当然这有个前提，就是每组都不能为空。

那若是有一组为空呢，图片就变成了这个样子

两个集合连起来也是偶边，自己集合连自己集合也是偶边，似乎无法连接了。

但是我们发现自己连自己横坐标差和纵坐标差都为偶数，和别的集合连得差都为偶数。

我们设同一集合的横坐标差为2k₁，纵坐标差为2k₂，不同集合的横坐标差为2k₁+1，纵坐标差是2k₂+1

根据距离公式d = √((x₁ - x₂) × (x₁ + x₂) + (y₁ - y₂) × (y₁ - y₂))进行计算（方便起见，直接算边长度的平方）。

同一集合相连 = (2k₁)² + (2k₂)² = 4(k₁² + k₂²)

不同集合相连 = (2k₁ + 1)² + (2k₂ + 1)² = 4(k₁² + k₂² + k₁ + k₂) + 2

很显然这两个是不会相等的。

那么如果不符合上一个情况，那么按x的奇偶性分组。

可是万一数据只有一个集合呢？

没事把数据缩小一倍就好了，到时候一定会有答案因为点坐标两两不同。

这样为什么可行呢？

因为同一个集合中的点的奇偶性都是相同的，那么我们将它们的最后一位舍弃也是符合原来的大小情况。

代码如下：

 #include <iostream>

 #include <cstdio>

 #include <algorithm>

 #include <cstring>

 #include <vector>

 #define rep(x, l, r) for(int x = l; x <= r; x++)

 #define repd(x, r, l) for(int x = r; x >= l; x--)

 #define clr(x, y) memset(x, y, sizeof(x))

 #define all(x) x.begin(), x.end()

 #define pb push_back

 #define mp make_pair

 #define MAXN 1005

 #define fi first

 #define se second

 #define SZ(x) ((int)x.size())

 using namespace std;

 typedef long long ll;

 typedef vector<int> vi;

 typedef pair<int, int> pii;

 const int INF =  << ;

 const int p = ;

 int lowbit(int x){ return x & (-x);}

 int fast_power(int a, int b){ int x; for(x = ; b; b >>= ){ if(b & ) x = 1ll * x * a % p; a = 1ll * a * a % p;} return x % p;}

 vi ans;

 int x[MAXN], y[MAXN], cnt[][];

 int main(){

     int n;

     scanf("%d", &n);

     rep(i, , n) scanf("%d%d", &x[i], &y[i]);

     while(){

         clr(cnt, );

         rep(i, , n) cnt[x[i] & ][y[i] & ]++;

         if(cnt[][] + cnt[][] >  && cnt[][] + cnt[][] > ){

             rep(i, , n)

                 if((x[i] & ) ^ (y[i] & )) ans.pb(i);

             printf("%d\n", SZ(ans));

             rep(i, , SZ(ans) - ) printf("%d ", ans[i]);

             puts("");

             return ;

         }

         if(cnt[][] + cnt[][] >  && cnt[][] + cnt[][] > ){

             rep(i, , n)

                 if(x[i] & ) ans.pb(i);

             printf("%d\n", SZ(ans));

             rep(i, , SZ(ans) - ) printf("%d ", ans[i]);

             puts("");

             return ;

         }

         rep(i, , n){

             x[i] >>= ;

             y[i] >>= ;

         }

     }

     return ;

 }

-E