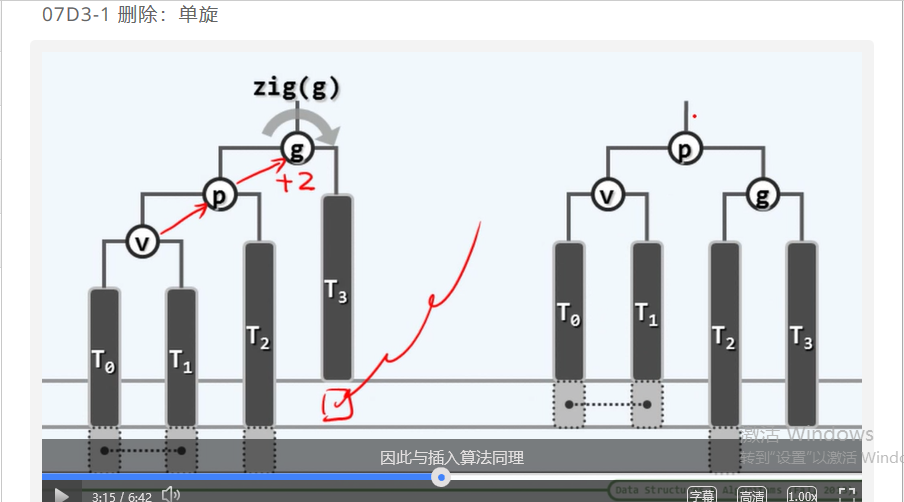
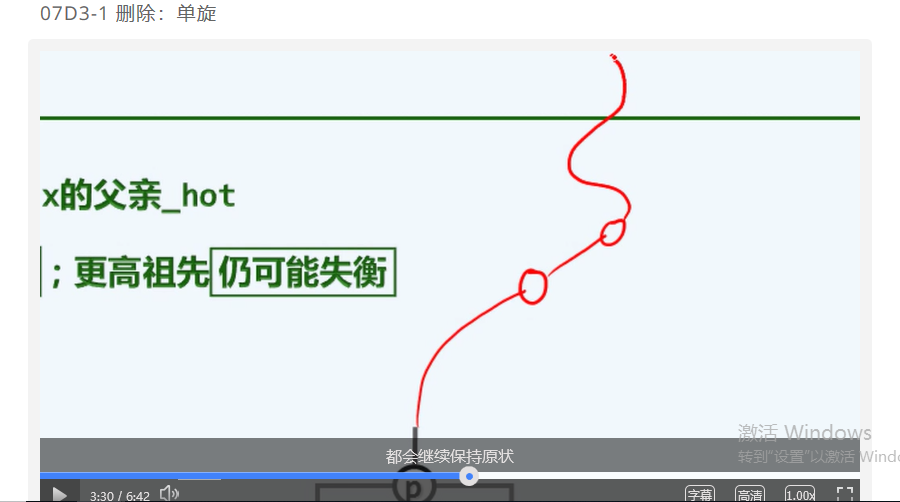
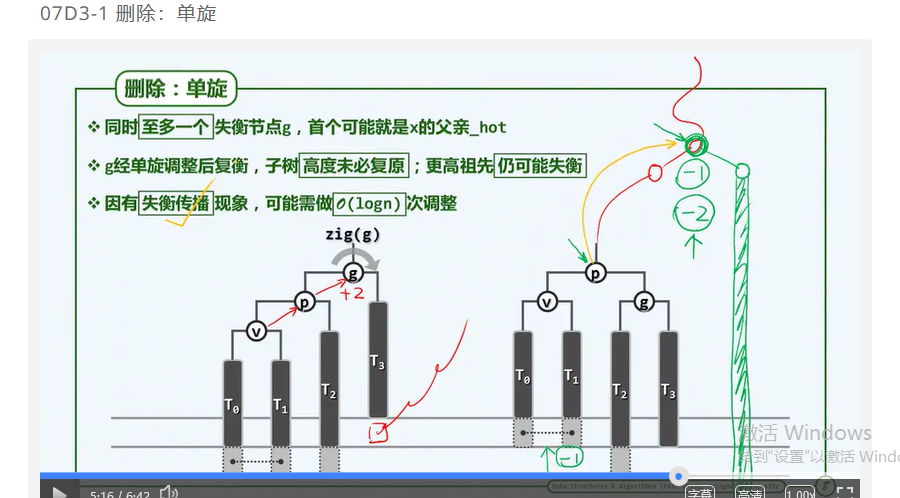
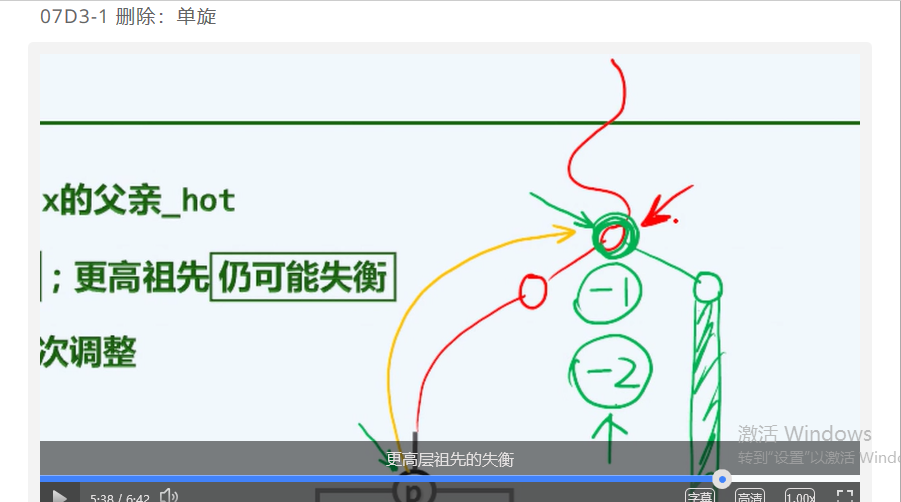
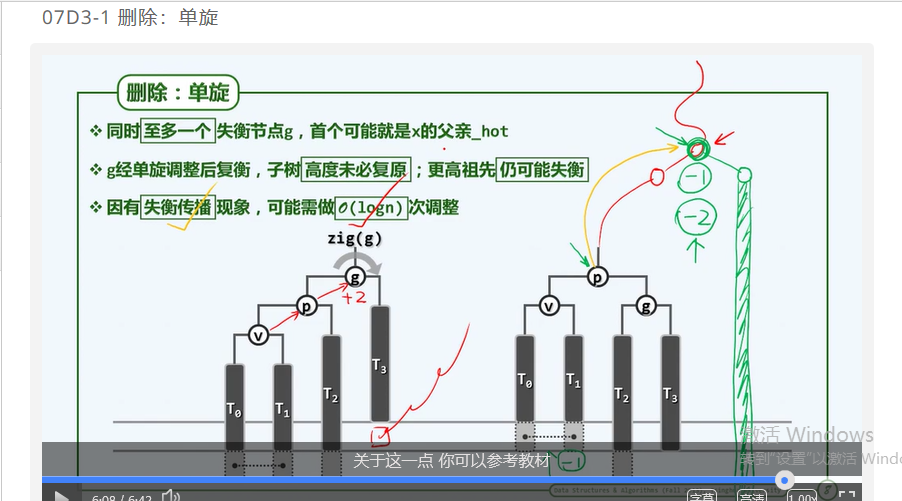
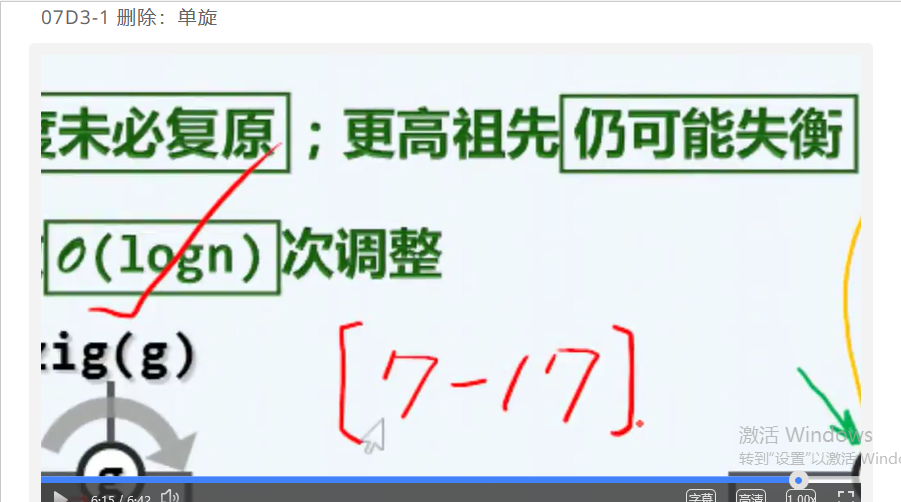
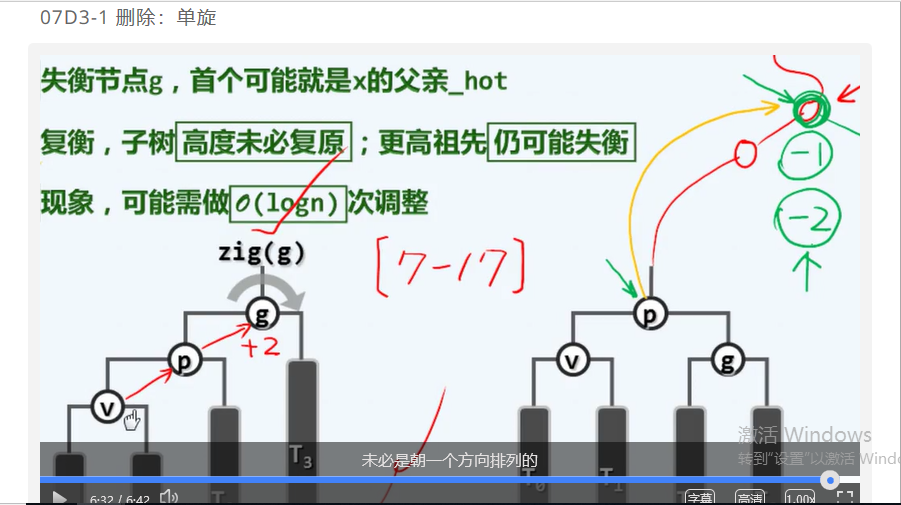
第七章 二叉搜索树 （d3）AVL树：删除
第七章 二叉搜索树 （d3）AVL树：删除的更多相关文章
- 从二叉搜索树到AVL树再到红黑树 B树
这几种树都属于数据结构中较为复杂的,在平时面试中,经常会问理解用法,但一般不会问具体的实现,所以今天来梳理一下这几种树之间的区别与联系,感谢知乎用户@Cailiang,这篇文章参考了他的专栏. 二叉查 ...
- 算法二叉搜索树之AVL树
最近学习了二叉搜索树中的AVL树,特在此写一篇博客小结. 1.引言 对于二叉搜索树而言,其插入查找删除等性能直接和树的高度有关,因此我们发明了平衡二叉搜索树.在计算机科学中,AVL树是最先发明的自平衡 ...
- 数据结构中的树(二叉树、二叉搜索树、AVL树)
数据结构动图展示网站 树的概念 树(英语:tree)是一种抽象数据类型(ADT)或是实作这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合.它是由n(n>=1)个有限节点组成一个具有 ...
- 【数据结构与算法Python版学习笔记】树——平衡二叉搜索树（AVL树）
定义 能够在key插入时一直保持平衡的二叉查找树: AVL树 利用AVL树实现ADT Map, 基本上与BST的实现相同,不同之处仅在于二叉树的生成与维护过程 平衡因子 AVL树的实现中, 需要对每个 ...
- 第七章 二叉搜索树（d4）AVL树：(3+4)-重构
- 第七章 二叉搜索树 （d2）AVL树：插入
- 第七章 二叉搜索树 （d1）AVL树：重平衡
- 第七章 二叉搜索树（b3）BST：删除
- 第七章 二叉搜索树（c）平衡与等价
随机推荐
- bzoj2048 书堆
Description Input 第一行正整数 N M Output 一行(有换行符),L,表示水平延伸最远的整数距离 (不大于答案的最大整数) 贪心地把最高的书尽量向右放可以得到最优解,因而最高的 ...
- shell 10流程控制
if 判断 if #shell #!/bin/sh a=5 if [[ $a > 3 ]];then echo "$a>3" fi #写成一行 if [[ $a < ...
- Appium+python自动化8-Appium Python API
Appium+python自动化8-AppiumPython API 前言: Appium Python API全集,不知道哪个大神整理的,这里贴出来分享给大家. 1.contexts conte ...
- html_常用技巧总结
============= 博客大全: 脚本之家:http://www.jb51.net/list/list_233_104.htm 红黑联盟: http://www.2cto.com/kf/yid ...
- Vue 路由的编程式导航与history模式
编程式导航 注意:官方文档写错了 通过javascript跳转 //第一种跳转方式 // this.$router.push({ path: 'news' }) // this.$router.pus ...
- RBF神经网络和BP神经网络的关系
作者:李瞬生链接:https://www.zhihu.com/question/44328472/answer/128973724来源:知乎著作权归作者所有.商业转载请联系作者获得授权,非商业转载请注 ...
- redis windows dll 下载
https://pecl.php.net/package/redis http://blog.csdn.net/leesin2011/article/details/72801629 http://w ...
- spark 应用程序部署工具 spark-submit
打包 Spark application 使用spark-submit启动Spark application spark-submit usage spark-submit option 运行模式相关 ...
- 代码： js日期
日期格式化 (new Date()).Format("yyyy-MM-dd hh:mm:ss.S") ==> 2015-11-16 08:09:04.423 (new Dat ...
- 42. linux下数据库服务启动
进到bin目录运行 emctl start dbconsole oracle@suse92:~> sqlplus /nolog SQL*Plus: Release 9.2.0.4.0 - Pro ...