洛谷P1387 最大正方形

题目描述

题目链接：https://www.luogu.org/problemnew/show/P1387

在一个n*m的只包含0和1的矩阵里找出一个不包含0的最大正方形，输出边长。

输入输出格式

输入格式：

输入文件第一行为两个整数n,m（1<=n,m<=100），接下来n行，每行m个数字，用空格隔开，0或1.

输出格式：

一个整数，最大正方形的边长

输入输出样例

输入样例#1：

4 4
0 1 1 1
1 1 1 0
0 1 1 0
1 1 0 1

输出样例#1：

2

算法解析：

来源：http://www.cnblogs.com/CXSheng/p/7801313.html

本题也可以参考洛谷题解

动态规划，求什么设什么。

设maxSize[i][j] = 以a[i][j]为右下角的最大正方形边长，

则maxSize[i][j] = k代表着a[i][j]左上方k*k区域内的数字都是1，

起初我想，如果a[i][j]是1，那么就可以把maxSize[i-1][j-1]代表的一大片矩形的边长扩大1.

即maxSize[i][j]=

①  0 ，a[i-1][j-1]==0 or 边界；

②  maxSize[i-1][j-1]+1 , a[i-1][j-1]!=0；

但是!这是片面的，因为我忽略了a[i][j]正上方和正左方是否存在0的情况。

如图：

假设我们要求maxSize[i][j]对应着最右下角的红点，

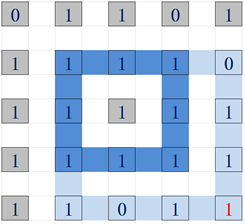
浅蓝色的圈是maxSize[i-1][j-1]对结果的影响；

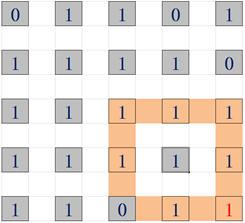
橙色的圈是a[i][j]正上方连续的1对结果的影响；

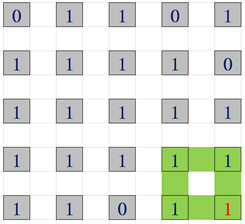
绿色的圈是a[i][j]正左方连续的1对结果的影响；

总图如下：

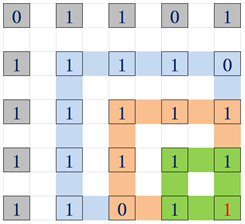
去三个值中最小的，记入maxSize[i][j]

综上可知，更新设定：

当a[i][j]为1时：

设maxSize[i][j] = 以a[i][j]为右下角的最大正方形边长，

LeftNum1[i][j] = a[i][j]（不包括）正左边连续1的个数，

UpNum1[i][j] = a[i][j]（不包括）正上方边连续1的个数，

于是maxSize[i][j] = min（maxSize[i-1][j-1]+1,leftNum1[i][j]+1,upNum1[i][j]+1）

注意边界情况即可。

 #include<stdio.h>
 #define MAXN 100
 #define MAXM 100
 int array[MAXN+][MAXM+]={};
 int maxSize[MAXN+][MAXM+]={};
 int leftNum1[MAXN+][MAXM+]={};
 int upNum1[MAXN+][MAXM+]={};
 int n,m;
 int Figure(int tempN,int tempM)
 {
     if(tempN-==||tempM-==||array[tempN-][tempM-]==)
         return ;
     int min=maxSize[tempN-][tempM-]+;
     if(leftNum1[tempN][tempM]+<min)
         min=leftNum1[tempN][tempM]+;
     if(upNum1[tempN][tempM]+<min)
         min=upNum1[tempN][tempM]+;
     return min;
 }
 void tPrint()
 {
 /*    int i,j;
     printf("\n");
     for(i=1;i<=n;i++)
     {
         for(j=1;j<=m;j++)
             //printf("%d ",[i][j]);
             printf("%d ",upNum1[i][j]);//==============
         printf("\n");
     }
     printf("\n");*/
 }
 int main()
 {
     int i,j;
     scanf("%d%d",&n,&m);
     int maxans=;
     for(i=;i<=n;i++)
         for(j=;j<=m;j++)
             scanf("%d",&array[i][j]);
     for(i=;i<=n;i++)
         for(j=;j<=m;j++)
         {
             if(j==||array[i][j]==)
                 leftNum1[i][j]=;
             else
             {
                 if(array[i][j-]==)
                     leftNum1[i][j]=;
                 else
                     leftNum1[i][j]=leftNum1[i][j-]+;
             }

             if(i==||array[i][j]==)
                 upNum1[i][j]=;
             else
             {
                 if(array[i-][j]==)
                     upNum1[i][j]=;
                 else
                     upNum1[i][j]=upNum1[i-][j]+;
             }
         }
     for(i=;i<=n;i++)
         for(j=;j<=m;j++)
         {
             maxSize[i][j]=Figure(i,j);
             if(maxSize[i][j]>maxans)
                 maxans=maxSize[i][j];
         }
     tPrint();
     printf("%d\n",maxans);
     return ;
 }

类似参考题目：

洛谷P1736 创意吃鱼法  题解