2013Hulu校园招聘笔试题

填空题：
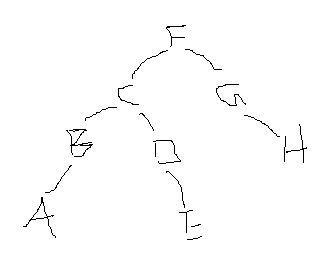
1、中序遍历二叉树，结果为ABCDEFGH，后序遍历结果为ABEDCHGF，先序遍历结果为?  FCBADEGH  如下图所示：

2、对字符串HELL0_HULU中的字符进行二进制编码，使得字符串的编码长度尽可能短，最短长度为？；（哈弗曼编码）1*4+1*4+1*3+3*2+2*2+2*2=25

3、对长度12的有序数组进行二分查找，目标等概率出现在数组的每个位置上，则平均比较次数为？37/12；(1*1 + 2*2 + 4*3 + 5*4)/12 = 37/12
4、一副扑克（去王），每个人随机的摸两张，则至少需要多少人摸牌，才能保证有两个人抽到同样的花色。

分析：，4+C(4,2)=10，抽屉原理

每个人摸到的两张牌的花色有10种情况:
两张红桃、两张黑桃、两张方块、两张梅花、红桃和黑桃、红桃和方块、红桃和梅花、黑桃和方块、黑桃和梅花、方块和梅花。
若10个人摸到的牌的花色分别是上述10种情况,则10个人中没有两个人摸到的牌的花色相同。
若有11个人摸牌,由抽屉原理可知至少有两个人摸到的牌的花色相同。

5、x个小球中有唯一一个球较轻，用天平秤最少称量y次能找出这个较轻的球，写出y和x的函数表达式y=f(x)

分析：y=log3(x)
6、3的方幂及不相等的3的方幂的和排列成递增序列1,3,4,9,10,12,13……，写出数列第300项

分析：设3的x次幂时为第300项，假设要求第3项那么x+C(x,2)=3，即：x^2+x-6=0，解得：x=2，同理得出x+C(x,2)=300，解得：x=24。。。。。。3^24左右吗

3^8+3^5+3^3+12
7、无向图G有20条边，有4个度为4的顶点，6个度为3的顶点，其余顶点度小于3，则G有多少个顶点？

20条边得出结点总数为40
去除4个4度，6个3度，还剩6
因为题上说其余结点度数都小于3，所以度数最大为2
所以最少还有3个结点，每个结点度数都为2
4＋6＋3＝13

8、桶中有M个白球，小明每分钟从桶中随机取出一个球，涂成红色（无论白或红都涂红）再放回，问小明将桶中球全部涂红的期望时间是？

分析：E(1)=1 //拿到第一个白球并将它涂红的期望时间
E(2)=M/M-1 //拿到第2个白球并将它涂红的期望时间
E(3)=M/M-2 //拿到第3个白球并将它涂红的期望时间
...
E(M)=M/1 //拿到第M个白球并将它涂红的期望时间
E(total)=E(1)+E(2)+...+E(M)=M(1+1/2+1/3+...+1/M)=M*(ln(M)+O(1))

9、煤矿有3000吨煤要拿到1000公里远的市场上卖，有一辆火车可以用来运煤，火车最多能装1000吨煤，且火车本身需要烧煤做动力，每走1公里消耗1吨煤，如何运煤才能使得运到市场的煤最多，最多是多少？533

如果你一开始就觉得不太可能的话，这是很正常的。不过我不知道你还会不会继续思考下去，如果你不想思考下去了，那么我很为你担忧，因为你可能并不是一个不善于思考的人，而是一个畏难的人，还有可能是一个容易放弃的人。这对于你做好 一个需要大量思考的工作的程序员来说可能并不适合。

我一开始也觉得不可能，后来想了一想，想到一个解法可以最多运送500吨煤到市场，方法如下：

装1000吨煤，走250公里，扔下500吨煤，回矿山。装1000吨煤，走到250公里处，拿起250吨煤继续向前到500公里处，扔下500吨煤，回矿山。此时火车上还有250吨，再加上在250公里处还有250吨煤，所以，火车是可以回矿山的。装上最后1000吨煤，走到500公里处，装上那里的500吨煤，然后一直走到目的。

于是，你最多可以运送500吨煤到市场（当然，火车也回不去了，因为那矿山没有煤了）

更好的一种思路是:
1.确定到底要运几次.
3次.推理过程略去。
所以包括往返两次和第三次直接到目的地。

2.确定每次火车的出发和返回的状态和目的：

2.1第一次出发满载1000，返回不剩煤。设第一次出发到达的地点距离起点x公里，目的：在路上留下头两次往返和第三次经过时足够支持火车走这段x公里的煤，所以5x=1000，x=200
2.2第二次出发满载1000，返回不剩煤。设第二次出发到达的地点距离起点x+y公里,目的：在路上留下第二次往返和第三次经过时足够支持火车走这段y公里的煤, 所以3y=1000，y约等于333
2.3第三次出发满载1000，直接到目的地。前200+333公里消耗的煤都补充上了，就是可以带到目的地的煤了，。

至于沿途放的煤，每次放的总量确定了，放的方法很多啊。

10、1,2,3,4…..n，n个数进栈，有多少种出栈顺序，写出递推公式（写出通项公式不得分）

令h(0)=1,h(1)=1，catalan数满足递推式[1]：
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)h(0) (n>=2)
例如：h(2)=h(0)*h(1)+h(1)*h(0)=1*1+1*1=2
h(3)=h(0)*h(2)+h(1)*h(1)+h(2)*h(0)=1*2+1*1+2*1=5
另类递推式[2]：
h(n)=h(n-1)*(4*n-2)/(n+1);
递推关系的解为：
h(n)=C(2n,n)/(n+1) (n=0,1,2,...)
递推关系的另类解为：
h(n)=c(2n,n)-c(2n,n+1)(n=0,1,2,...)

11、宇宙飞船有100,000位的存储空间，其中有一位有故障，现有一种Agent可以用来检测故障，每个Agent可以同时测试任意个位数，若都没有故障，则返回OK，若有一位有故障，则失去响应。如果有无限多个Agent可供使用，每个Agent进行一次检测需要耗费1小时，现在有2个小时时间去找出故障位，问最少使用多少个Agent就能找出故障。

首先 大家都知道n个agent一次最多测试2^n个位（经典老题：小白鼠测试毒药瓶），假设总共N个位那么第1个小时内可以用x个agent来测试2^x段（每个段含有 N/（2^x） 位），选出包含坏位的那个段，在第二小时内检出坏位 ，那么 （N/（2^x)) <= （2^x）,所以 x=log2(N) /2 的最小上限 。所以此题中 x = 9.

举例说明： 如果是64位（2^6），那么用3个agent就可以了。
第一次： 3个agent把64为分成8（2^3）段，每段8个位，
0-7位不连接，8-15位（1号段）连接1号agent（2^0），16-23位（2号段）连接2号agent(2^1),24-31位（3号段）连接1,2号agent(2^1+2^0)，......,56-63位（7号段）连接1,2，3号agent(2^2+2^1+2^0)，一个小时后根据没有返回的agent组合确定是哪一段坏了
第二次：通过3个agent把坏段（8位）中唯一的坏位检测出来

如果是128位（2^7），那么用4个agent就可以了。
第一次： 4个agent把128为分成16（2^4）段，每段8个位，
0-7位不连接，8-15位（1号段）连接1号agent（2^0），16-23位（2号段）连接2号agent(2^1),24-31位（3号段）连接1,2号agent(2^1+2^0)，......,56-63位（7号段）连接1,2，3号agent(2^2+2^1+2^0)，......,120-128位（15号段）连接1,2，3,4号agent(2^3+2^2+2^1+2^0)，一个小时后根据没有返回的agent组合确定是哪一段坏了
第二次：通过不小于3个的agent把坏段（8位）中唯一的坏位检测出来

大题：
1、n个数，找出其中最小的k个数，写出代码，要求最坏情况下的时间复杂度不能高于O(nlogk)

各种思路:

1. 对n个数排序，取前k个。这里假设不考虑计数排序、基数排序和桶排序等非比较为基础的算法，最先想到的快速排序(QuickSort)时间复杂度O(nlogn)，空间复杂度O(1)。

2. 用数组B保存前k个数，然后从第k+1个数开始，假设为第i个数，每次都找出数组B中的最大数，当第i个数小于数组B中的最大数则替换。这样的时间复杂度是O((n-k)*k)=O(nk)，空间复杂度O(k)。

3. 根据想法2我们可能很自然的发现其中找数组B最大数的时间复杂度可以简化，就是维护一个大小为k的最大堆(注意，确实是最大堆而不是最小堆，因为最大堆的元素在堆顶)。建堆时间复杂度O(k),然后从第k+1个数开始，假设为第i个数，当第i个数小于堆顶元素则替换并调整堆(logn)，因此总时间复杂度是O(k + (n-k)*logk) = O(n*logk)，空间复杂度O(k)。

4. 我们当然也可以将A中所有元素建立一个最小堆( 时间O(n) )，再取k次对顶元素并调整堆(k*logk)。这样时间复杂度O(n + k*logk)，空间复杂度O(n)。

5. 我们将A数组放入一个优先级队列，再进行k次pop()动作。其实这个想法本质和4是一样的，因为优先级队列就是利用堆实现的。O(n + k*logk)，空间复杂度O(n)。

6. 我们当然也可以不用大小为n的优先级队列，只需要用到k+1大小的(考虑空间复杂度)，先将前k个数push进这个优先级队列，而后从第k+1个数开始的每一个数，先push进队列再马上pop一个。时间复杂度待分析(不知道内部实现原理)，但是使用优先级队列的优势是代码可靠性高并且简单。

7. 根据快速排序的思想，随机从数组A中选取一个元素作为划分元素(枢纽元素)X，划分数组A为小于等于X和大于等于X的两部分：LA <= X <= UA，此时有以下三种情况: (1)如果LA的大小正好是k，那么LA就是我们要找的k个最小的元素；(2)如果LA的大小大于k，那么我们要找的k个元素肯定全部在LA内，因此继续对LA进行类似的划分；(3)如果LA的大小小于k，则LA内全部的元素都是我们要找的，并且还有部分元素(k-size(LA)-1个)在UA内，则我们继续对UA进行划分寻找剩下的k-size(LA)-1个元素。最坏情况时间复杂度O(n) (关于这个时间复杂度可以查询<算法导论>)。

2、写程序输出8皇后问题的所有排列，要求使用非递归的深度优先遍历。
3、有n个作业，a1,a2…..an，作业aj的处理时间为tj，产生的效益为pj，最后完成期限为dj，作业一旦被调度则不能中断，如果作业aj在dj前完成，则获得效益pj，否则无效益。给出最大化效益的作业调度算法。

分析：

先按照完成期限排序，然后用DP求解（其实就是稍微改变一下背包程序就可以了）。

DP[i,j]表示 j 时间之前做前i个任务可以获得的最大收益，

DP[i,j] = max(DP[i-1,j-t[i]] + P[i]，DP[i-1,j])，

如果j大于dj，则不用做状态转移了。

这样来看，状态转移O(1)，状态数量为O(n*m)，m为时间跨度。

 

分析： 
其实这个问题类似于01背包问题。
1.    将a1,a2,…,an按照dj值排序，从小到大。假设接下来的分析中，已经保证当i<j时，di<dj。添加d0=0。
2.    构建数组s[n][d[n]]，s[i][j]代表在j时间内，调度i个作业，所得最高效益值。初始时，令s[i][0] = 0（i = 0->n），s[0][j] = 0（j = 0->d[n]）。
3.    求s[i][j]的值，select[i][j]用于记录是否选择i。这里递归包含了一种思想：如果第i个作业被调度，那么最好使其在期限时正好结束，这样能够保证i之前的作业能够在更充裕的时间内被调度。

for i = ->n
    for j = ->d[i]
        //不调度i
        s[i][j] = s[i-][min(j, d[i-])]
        select[i][j] = false
        //调度i
        if j>t[i]
            if s[i][j] < s[i-][min(j-t[i], d[i-])]+p[i]
                s[i][j] = s[i-][min(j-t[i], d[i-])]+p[i]
                select[i][j] = true  

4.    最终s[n][d[n]]即为所求最高效益值。如果要求出所调度的作业序列，可以通过select取得。

注意d[i-1][j] 中j最多到达d[i-1], 所以要min(j-t[i], d[i-1])!!

 

 

http://s.yingjiesheng.com/m_hulu