java-信息安全（八）-迪菲-赫尔曼（DH）密钥交换【不推荐，推荐Oakley】

概述

信息安全基本概念：

• DH(Diffie–Hellman key exchange,迪菲-赫尔曼密钥交换)

DH

　　是一种安全协议,,一种确保共享KEY安全穿越不安全网络的方法，它是OAKLEY的一个组成部分。

　　这个机制的巧妙在于需要安全通信的双方可以用这个方法确定对称密钥。然后可以用这个密钥进行加密和解密。但是注意，这个密钥交换协议/算法只能用于密钥的交换，而不能进行消息的加密和解密。双方确定要用的密钥后，要使用其他对称密钥操作加密算法实际加密和解密消息。

　　Oakley算法是对Diffie-Hellman密钥交换算法的优化，它保留了后者的优点，同时克服了其弱点. Oakley算法具有五个重要特征： 它采用称为cookie程序的机制来对抗阻塞攻击. 它使得双方能够协商一个全局参数集合. 它使用了现时来保证抵抗重演攻击. 它能够交换Diffie-Hellman公开密钥. 它对Diffie-Hellman交换进行鉴别以对抗中间人的攻击.

DH算法具有两个吸引力的特征：

1. 仅当需要时才生成密钥，减小了将密钥存储很长一段时间而致使遭受攻击的机会；
2. 除对全局参数的约定外，密钥交换不需要事先存在的基础结构；

然而，该技术也存在许多不足：

1. 没有提供双方身份的任何信息；
2. 计算密集性，因此容易遭受阻塞性攻击，即对手请求大量的密钥。受攻击者花费了相对多的计算资源来求解无用的幂系数而不是在做真正的工作；
3. 没办法防止重演攻击；
4. 容易遭受中间人的攻击。第三方C在和A通信时扮演B；和B通信时扮演A。A和B都与C协商了一个密钥，然后C就可以监听和传递通信量。中间人的攻击按如下进行：

• B在给A的报文中发送他的公开密钥Y_B。
• C截获并解析该报文。C将B的公钥保存下来并给A发送报文，该报文具有B的用户ID但使用C的公钥Y_C，但仍按照好像是来自B的样子被发送出去。A收到C的报文后，将Y_C和B的用户ID存储在一块。类似地，C使用Y_C向B发送好像来自A的报文。
• B基于私钥X_B和Y_C计算共享密钥K_1，A基于私钥X_A和Y_C计算共享密钥K_2，C使用私钥X_C和Y_B计算K₁，并使用X_C和Y_A计算K₂。
• 从现在开始，C就可以转发A发给B的报文或转发B发给A的报文，在途中根据需要修改它们的密文。使得A和B都不知道他们在和C共享通信。

流程分析

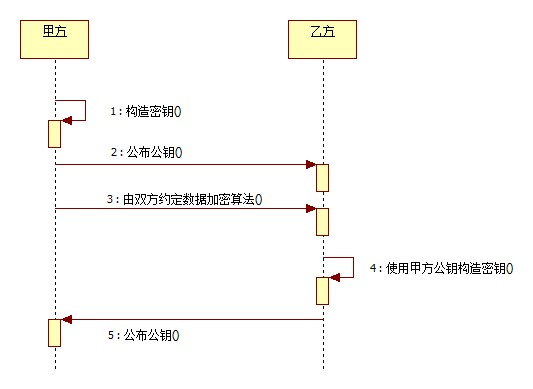
　　1.甲方构建密钥对儿，将公钥公布给乙方，将私钥保留；双方约定数据加密算法；乙方通过甲方公钥构建密钥对儿，将公钥公布给甲方，将私钥保留。

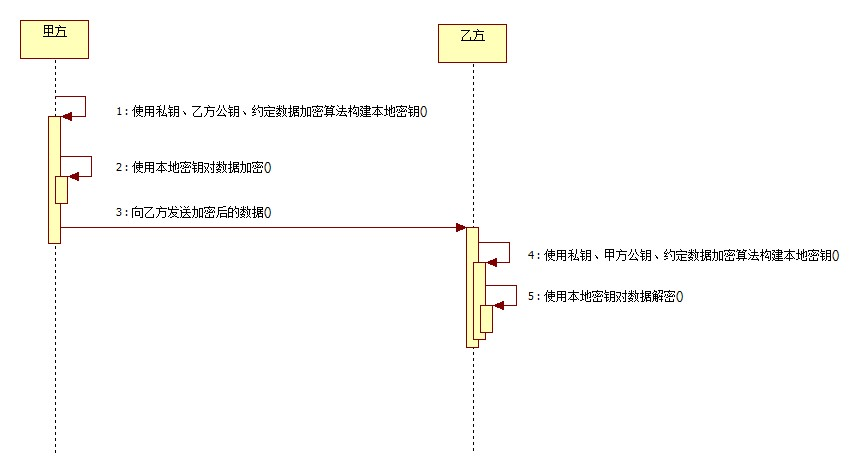
　　2.甲方使用私钥、乙方公钥、约定数据加密算法构建本地密钥，然后通过本地密钥加密数据，发送给乙方加密后的数据；乙方使用私钥、甲方公钥、约定数据加密算法构建本地密钥，然后通过本地密钥对数据解密。

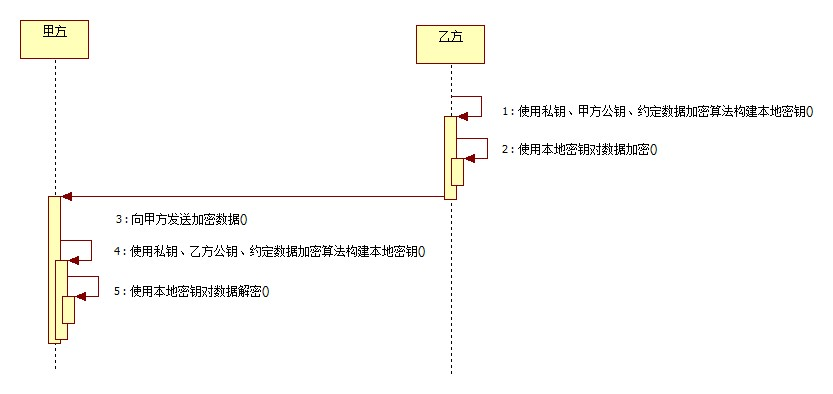
　　3.乙方使用私钥、甲方公钥、约定数据加密算法构建本地密钥，然后通过本地密钥加密数据，发送给甲方加密后的数据；甲方使用私钥、乙方公钥、约定数据加密算法构建本地密钥，然后通过本地密钥对数据解密。

代码实现

　　代码地址：https://github.com/bjlhx15/algorithm-sign.git

Oakley算法

是对Diffie-Hellman密钥交换算法的优化，它保留了后者的优点，同时克服了其弱点。

Oakley算法具有五个重要特征：

1、它采用称为cookie程序的机制来对抗阻塞攻击。

2、它使得双方能够协商一个全局参数集合。

3、它使用了现时来保证抵抗重演攻击。

4、它能够交换Diffie-Hellman公开密钥。

5、它对Diffie-Hellman交换进行鉴别以对抗中间人的攻击。

Oakley可以使用三个不同的鉴别方法：

1、数字签名：通过签署一个相互可以获得的散列代码来对交换进行鉴别；每一方都使用自己的私钥对散列代码加密。散列代码是在一些重要参数上生成的，如用户ID和现时。

2、公开密钥加密：通过使用发送者的私钥对诸如ID和现时等参数进行加密来鉴别交换。

3、对称密钥加密：通过使用某种共享密钥对交换参数进行对称加密，实现交换的鉴别。