已知大小分别为m、n的两个无序数组A、B和一个常数c，求满足A[i]+B[j]=c的所有A[i]和B[j]

方法一：枚举法。该方法是最容易、也是最简单的方法，枚举出数组A和数组B中所有的元素对，判断其和是否为c，如果是，则输出。

方法二：排序+二分查找法。首先，对两个数组中长度较大数组，不妨设为A，排序；然后，对于B中每个元素B[i]在A中二分查找c-B[i]，如果找到，直接输出。

方法三：排序+线性扫描法。首先，对A和B进行排序；然后用指针p从头扫描A，用指针q从尾扫描B，如果A[p]+B[q]==c，则输出A[p]+B[q]，且p++，q--；如果A[p]+B[q]>c，则q--；否则p++。
    代码如下：

#include "stdafx.h"
#include <stdio.h>
void sortArray(int a[], int n)
{
	if (a == NULL || n <= 0)
		printf("数组中无元素，排个毛啊。");
	else
	{
		int temp;
		for (int i = 0; i < n-1; i++)
		{
			for (int j = i + 1; j < n; j++)
			{
				if (a[i]>a[j])
				{
					a[i] = a[i] ^ a[j];
					a[j] = a[j] ^ a[i];
					a[i] = a[i] ^ a[j];
				}
			}
		}
	}
}
void findCouple(int a[], int b[], int An, int Bn,int sum)
{
	if (a == NULL || An <= 0 || b == NULL || Bn <= 0)
		printf("数组中无元素，找个毛啊。");
	else
	{
		for (int i = 0, j = Bn - 1; i < An, j >= 0;)
		{
			if (a[i] + b[j]>sum)
				j--;
			if (a[i] + b[j] == sum)
			{
				printf("%d,%d\n", a[i], b[j]);
				i++;
				j--;
			}
			if (a[i] + b[j] < sum)
				i++;
		}
	}
}
void main()
{
	int a[] = {1,3,1,5,2,0};
	int b[] = { 1, 4, 3, 1, 0, 1 };
	int An = sizeof(a) / sizeof(int);
	int Bn = sizeof(b) / sizeof(int);
	sortArray(a, An);
	sortArray(b, Bn);
	findCouple(a, b, An, Bn, 6);
	getchar();
}

　　效果如图：

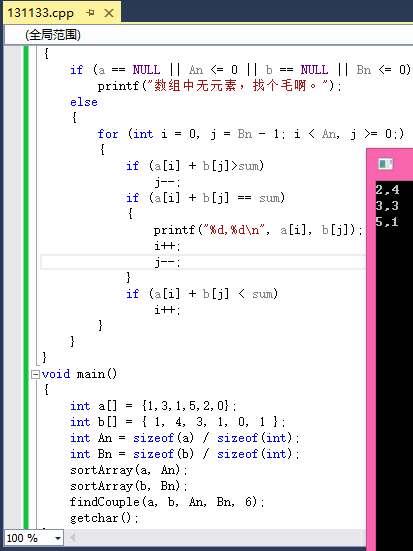
方法四：Hash法。首先，将两个数组中长度较小的数组，不妨设为A，保存到哈希表中，然后，对于B中每个元素B[i]，也采用相同的hash算法在哈希表中查找c-B[i]是否存在，如果存在，则输出.时间复杂度为O(m+n)，空间复杂度为O(min{m,n})。但这种算法有个问题，就是会出现重复。

代码如下：

#include "stdafx.h"
#include <iostream>
#include <map>
using namespace std;
void print_pairs_with_sum2(int A[], int B[], int m, int n, int sum)
{
	map<int, bool> hash_table;
	int *psmaller = A;
	int *pbigger = B;
	int nsmaller = (m >= n) ? n : m;
	int nbigger = (m >= n) ? m : n;
	if (m > n)
	{
		psmaller = B;
		pbigger = A;
	}
	for (int i = 0; i < nsmaller; i++)
	{
		hash_table.insert(pair<int, bool>(psmaller[i], true));
	}
	for (int i = 0; i < nbigger; i++)
	{
		if (hash_table.find(sum - pbigger[i])!= hash_table.end())
		{
			cout << "(" << pbigger[i] << "," << sum - pbigger[i] << ")" << endl;
		}
	}
}
void main()
{
	int a[] = { 1, 5, 4, 3, 2, 0 };
	int b[] = { 1, 4, 3, 1, 0, 1 ,};
	int m = sizeof(a) / sizeof(int);
	int n = sizeof(b) / sizeof(int);
	print_pairs_with_sum2(a, b, m, n, 6);
	getchar();
}

　　效果如图：