笔记 Bioinformatics Algorithms Chapter1

Chapter1 WHERE IN THE GENOME DOES DNA REPLICATION BEGIN 

 

一、

·聚合酶启动结构域会结合上游序列的一些位点，这些位点有多个，且特异，并且分布在两条链上。通过计算，找到出现频率最高的k-mer可能为为聚合酶结合位点：dnaA BOX。

但是如何定位Ori的大概位置呢？

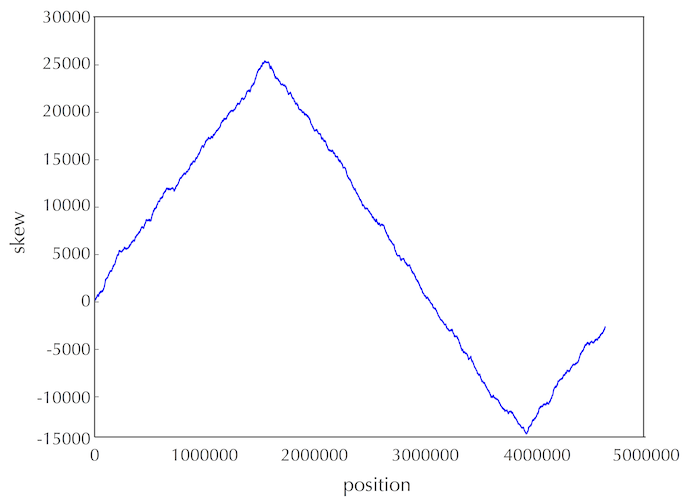
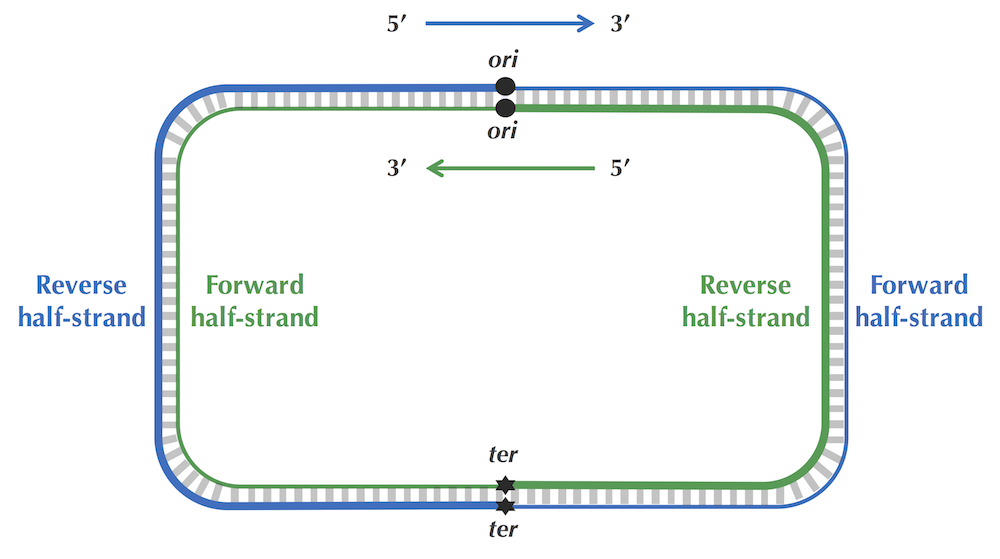
·DNA链复制的不对称性，其导致突变速率的不对称，使得有（forward链C->T，脱氨基）的趋势。由此，依据skew增的处于forward链，skew减的处于reverse链。（skew = G - C ，逢G+1 逢C-1）图中最低点代表Ori区域。

由此可以大致推测出ori的位置，然后在此位置内（100bp），寻找出现频率大的pattern，作为可能的dnaA box。

·由于k-mer之间，会有碱基的若干差异，故应使用能容错的计数方法。

二、

提出问题：The Clump Finding Problem

Find every k-mer that forms a clump in the genome.

ComputingFrequencies(Text, k) #一种遍历一次计算频率的‘桶’方法
        for i ← 0 to 4k − 1
            FrequencyArray(i) ← 0
        for i ← 0 to |Text| − k
            Pattern ← Text(i, k)
            j ← PatternToNumber(Pattern) #hash
            FrequencyArray(j) ← FrequencyArray(j) + 1
        return FrequencyArray

ComputingFrequencies(Text, k)这是一种计算kmer频率的方法

FindingFrequentWordsBySorting(Text , k) #排序法
        FrequentPatterns ← an empty set
        for i ← 0 to |Text| − k
            Pattern ← Text(i, k)
            Index(i) ← PatternToNumber(Pattern)
            Count(i) ← 1
        SortedIndex ← Sort(Index)
        for i ← 1 to |Text| − k
            if SortedIndex(i) = SortedIndex(i − 1)
                Count(i) = Count(i − 1) + 1
        maxCount ← maximum value in the array Count
        for i ← 0 to |Text| − k
            if Count(i) = maxCount
                Pattern ← NumberToPattern(SortedIndex(i), k)
                add Pattern to the set FrequentPatterns
        return FrequentPatterns
       

FindingFrequentWordsBySorting(Text , k)这是另一种计算kmer频率的方法

一种容错的频率计算方法

ClumpFinding(Genome, k, L, t)
        FrequentPatterns ← an empty set
        for i ← 0 to 4k − 1
            Clump(i) ← 0
        for i ← 0 to |Genome| − L
            Text ← the string of length L starting at position i in Genome
            FrequencyArray ← ComputingFrequencies(Text, k)
            for index ← 0 to 4k − 1
                if FrequencyArray(index) ≥ t
                    Clump(index) ← 1
        for i ← 0 to 4k − 1
            if Clump(i) = 1
                Pattern ← NumberToPattern(i, k)
                add Pattern to the set FrequentPatterns
        return FrequentPatterns

我们不用每次挪动一位搜寻窗就重新计算kmer频率，搜寻窗每挪一位，原来的第一个kmer将少一个，结尾后一个kmer将多一个

BetterClumpFinding(Genome, k, t, L)
        FrequentPatterns ← an empty set
        for i ← 0 to 4k − 1
            Clump(i) ← 0
        Text ← Genome(0, L)
        FrequencyArray ← ComputingFrequencies(Text, k)
        for i ← 0 to 4k − 1
            if FrequencyArray(i) ≥ t
                Clump(i) ← 1
        for i ← 1 to |Genome| − L
            FirstPattern ← Genome(i − 1, k)
            index ← PatternToNumber(FirstPattern)
            FrequencyArray(index) ← FrequencyArray(index) − 1
            LastPattern ← Genome(i + L − k, k)
            index ← PatternToNumber(LastPattern)
            FrequencyArray(index) ← FrequencyArray(index) + 1
            if FrequencyArray(index) ≥ t
                Clump(index) ← 1
        for i ← 0 to 4k − 1
            if Clump(i) = 1
                Pattern ← NumberToPattern(i, k)
                add Pattern to the set FrequentPatterns
        return FrequentPatterns