HGOI 20181101题解
/*
又是爆0的一天(不知道今年高考难不难,反正今天(信息学)真的难!)
*/

solution:对于两个数相加,有一个显然的结论就是要么不进位(相对于位数大的),要么(进最多一位)
然后对于整个数组先排序,然后枚举每一个数,在它的前面找到和他相加进1位的点,讨论不变位和进一位累加求和即可
由于数列有序对于最左边的p满足f(a[p]+a[now])=f(a[now])+1对于他的右边所有的数都符合进一位的条件,这样可以二分查找找到最左端的点
# pragma GCC optimze()
# include<bits/stdc++.h>
# define int long long
using namespace std;
const int MAXN=1e6+;
int n,a[MAXN];
inline int read()
{
int X=,w=;char c=;
while (!(c>=''&&c<='')) w|=c=='-',c=getchar();
while (c>=''&&c<='') X=(X<<)+(X<<)+(c^),c=getchar();
return w?-X:X;
}
int fun(int x)
{
int ret=;
while (x){ ret++; x/=;}
return ret;
}
int find(int sl,int sr,int id)
{
int l=sl,r=sr,ans=-;
int tmp=fun(a[id])+;
while (l<=r) {
int mid=(l+r)/;
if (fun(a[mid]+a[id])==tmp) r=mid-,ans=mid;
else l=mid+;
}
return ans;
}
signed main()
{
n=read();
for (int i=;i<=n;i++) a[i]=read();
sort(a+,a++n);
int ans=;
for (int i=;i<=n;i++) {
int p=find(,i-,i),tmp=fun(a[i]);
if (p==-) ans+=tmp*(i-);
else ans+=(tmp+)*(i-p)+tmp*(p-);
}
cout<<ans<<endl;
return ;
}

solution:这个题有一个结论,就是对于全集U={所有人}的2n个子集,存在tot个满足下面关系的子集
子集中所有的权重加起来不足m,但是从其他不选的人随便拿一个放入子集权重都能大于等于m,最终统计出的tot就是答案
也就是最少需要锁的个数。
上面的结论是我们构造出来的,然后我们需要证明这个结论。
现在首先是两个性质的事情,
数学上我们定义:
- 证明条件:通过所有的证明条件推出一个结论的条件全集。
- 必要条件:是证明条件的子集,所有的必要条件的全集就是证明条件,无论是什么证明方法,都需要的条件。
- 充分条件:证明条件是充分条件的子集,也就是满足充分条件的一定满足必要条件。
(如证明一个图形是直角三角形,必要条件可以是:这个图形是三角形,充分条件可以是:这个图形是等腰RT三角形)
有这样的结论:
- 所有有这样的关系:必要条件⊆证明条件⊆充分条件
- 如果一个条件集既是必要条件又是充分条件,那么这个条件必然是证明条件。
- 我们证明必要条件就是证明满足这样的条件不一定可以构造出合法答案(找到反例)
- 我们证明充分条件就是在充分条件下,构造一种方法让其条件合法
回到题目,我们来证明上面的必要性和充分性,
- 必要性:由于上面任一子集的权值和都不足m,那么他们都至少缺一把锁不能开启,若锁的个数不足所有合法子集数把锁,那么由鸽巢原理可知,必然有两个子集缺的是同一把锁,然后如果我们把这两个子集拼起来,那么他们的权值和已经大于m了却不能打开全部的锁,与题意矛盾,故证明必要性。(可知锁至少是tot个)
- 充分性:(如果锁恰好是tot那么一定存在一种合法的分配方式让他们满足题设)假设我们将每一把锁(tot个)上都写一个居民的子集,然后令一个居民拥有除了这个居民对应的一把钥匙,然后任取一个集合和这个居民配对显然可以开启所有的锁,所有其充分性得证。
- 所以我们提出的条件是充分必要条件,所有就是证明条件,证必。
# include <bits/stdc++.h>
# define int long long
using namespace std;
const int MAXN=;
int a[MAXN],t[MAXN];
int ans,n,m;
bool check()
{
int sum=;
for (int i=;i<=n;i++) if (t[i]) sum+=a[i];
if (sum>=m) return false;
for (int i=;i<=n;i++)
if (t[i]==&&sum+a[i]<m) return false;
return true;
}
void dfs(int dep)
{
if (dep==n+) { if (check()) ans++; return;}
t[dep]=;dfs(dep+);
t[dep]=;dfs(dep+);
}
signed main()
{
scanf("%d%d",&n,&m);
for (int i=;i<=n;i++) scanf("%d",&a[i]);
memset(t,,sizeof(t));
ans=;
dfs();
cout<<ans<<endl;
return ;
}

solution:
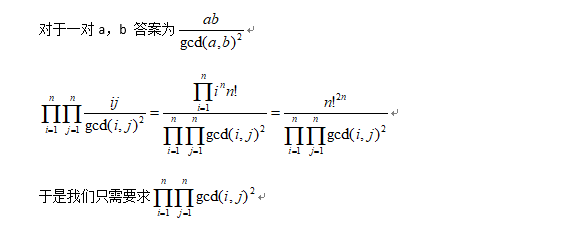



HGOI 20181101题解的更多相关文章
- HGOI 20181028 题解
HGOI 20181028(复赛备考) /* 真是暴力的一天,最后一题MLE?由于数组开得太大了!!! 270滚粗 考场上好像智商高了很多?!(假的) */ sol:暴力求解,然后没有数据范围吐槽一下 ...
- HGOI 20190310 题解
/* 又是又双叒叕WA的一天... 我太弱鸡了... 今天上午打了4道CF */ Problem 1 meaning 给出q组询问,求下列函数的值$ f(a) = \max\limits_{0 < ...
- HGOI 20190303 题解
/* 记一串数字真难. 5435 今天比赛又是hjcAK的一天. 今天开题顺序是312,在搞T1之前搞了T3 昨天某谷月赛真是毒瘤. 但是讲评的同学不错,起码T4看懂了... 构造最优状态然后DP的思 ...
- HGOI 20180224 题解
/* The Most Important Things: ljc chat with fyh on QQTa说期末考Ta数学74分感觉不好但是我觉得fyh是地表最强的鸭~~(of course en ...
- HGOI 20190218 题解
/* 又是AK局... hjc又双叒叕AK了... Hmmm...我侥幸 */ Problem A card 给出无序序列a[]可以选择一个数插入到合适的位置作为一次操作,至少多少次操作后可以把序列变 ...
- HGOI 20190217 题解
/* for me,开训第一天 /beacuse 文化课太差被抓去补文化课了... 看一眼题 : AK局? 但是,Wa on test #10 in problem C 290! (就差那么一咪咪) ...
- HGOI 20181103 题解
problem:把一个可重集分成两个互异的不为空集合,两个集合里面的数相乘的gcd为1(将集合中所有元素的质因数没有交集) solution:显然本题并不是那么容易啊!考场上想了好久.. 其实转化为上 ...
- HGOI 20191108 题解
Problem A 新婚快乐 一条路,被$n$个红绿灯划分成$n+1$段,从前到后一次给出每一段的长度$l_i$,每走$1$的长度需要$1$分钟. 一开始所有红绿灯都是绿色的,$g$分钟后所有红绿灯变 ...
- HGOI 20191107 题解
Problem A 树状数组 给出下列$C++$代码: 设区间加操作$modify(l,r)$为调用两次$update(r,1)$和$update(l-1,-1)$ 设$f(l,r)$表示在初始$cn ...
随机推荐
- SqlServer执行大的数据库脚本出错解决方法
如果执行线上项目拷下来sqlserver的.sql的数据库脚本文件,如果文件较大时,那么就会报错内存不足之类的. 这时可以在命令提示符使用命令来执行脚本文件.切记,执行前先改一下数据库存放位置! 命令 ...
- WPF之Manipulation
原文:WPF之Manipulation 需求:现,在窗口下有一个StackPanel控件. 1.可以拖动. 2.可以展开及收缩(不仅仅可以拖动还可以点击) 3.窗口向坐标轴一样分四个象限,在不同的区域 ...
- EZ 2018 01 14 2018noip第四次膜你赛
这次惨烈的炸了个精光(只有20),然后对我的OI想法造成了巨大的转折. (以上有点作,其实我只是再也不用vector存图了而已(用邻接表)) 难度很不均匀,而且题型很狗(还有结论题???) T1 坑人 ...
- mfc CImageList和CListCtrl
知识点: CImageList类的运用 CListCtrl添加图标 一.CImageList CImageList*SetImageList(CImageList*pImageList,int nIm ...
- 解决 配置springmvc拦截所有请求后请求静态资源404的问题
<servlet-mapping> <servlet-name>spring-servlet</servlet-name> <url-pattern>/ ...
- [CF1067D]Computer Game[凸包/斜率优化+倍增+矩阵乘法]
题意 你有 \(n\) 个任务,初始收益为 \(a\) ,共 \(t\) 轮游戏,每轮可以选择完成一个任务(可以做多次),完成之后可以给任意任务升级,升级之后的任务收益为 \(b\) ,每个任务还有完 ...
- 使用不同的方法计算TF-IDF值
摘要 这篇文章主要介绍了计算TF-IDF的不同方法实现,主要有三种方法: 用gensim库来计算tfidf值 用sklearn库来计算tfidf值 用python手动实现tfidf的计算 总结 之所以 ...
- 对html第一次尝试
1.对于写文档 修改后缀为html,双击进入为网页模式. 2.编写网页 1)新建 2)基本格式 <!DOCTYPE html><!-- ...
- JMeter采用NON GUI模式时如何记录并查看错误
在GUI模式下执行JMeter测试时,我们可以通过添加View Results Tree组件来查看JMeter请求的各类详情.那如果在正式测试场景中,当我们采用NON GUI模式时,遇到了断言或其他错 ...
- C# List left join
public class Test1 { public int ID { get; set; } public string Name { get; set; } } public class Tes ...
