[ML学习笔记] 决策树与随机森林（Decision Tree&Random Forest）

[ML学习笔记] 决策树与随机森林（Decision Tree&Random Forest）

##决策树

决策树算法以树状结构表示数据分类的结果。每个决策点实现一个具有离散输出的测试函数，记为分支。

一棵决策树的组成：根节点、非叶子节点（决策点）、叶子节点、分支

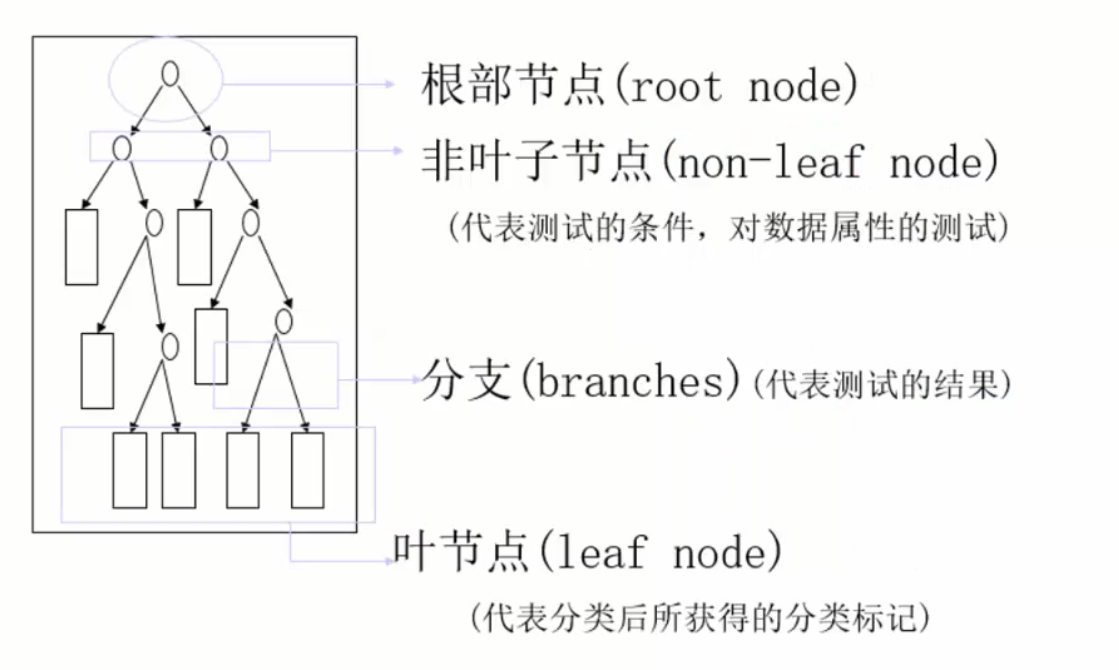
算法分为两个步骤：1. 训练阶段（建模） 2. 分类阶段（应用）

###熵的概念

设用P(X)代表X发生的概率，H(X)代表X发生的不确定性，则有：P(X)越大，H(X)越小；P(X)越小，H(X)越大。

信息熵的一句话解释是：消除不确定性的程度。熵 =$ -\sum_{i=1}^nP_i\log(P_i)$

当熵较小时表示集合较纯，分类效果较好。因此，构造树的基本想法是随着树深度的增加，节点的熵迅速降低，降低的速度越快越好，这样才有望得到一棵高度最矮的决策树。

###如何划分

为了满足上述基本想法，想要选取一个划分标准来为当前集合分类，需要定义一个指标来评判分类效果。

常见的有以下三种指标：

ID3：信息增益（划分前熵值 - 划分后熵值）

C4.5：信息增益率（信息增益 / 划分前的熵值）

CART：Gini系数

最传统的做法就是选取信息增益最大的特征作为划分节点（ID3），但它在一些情况下不适用，比如当存在某些特征的取值很多、每个取值对应的样本数据很少（如id值，会将N个用户划分为N类），此时虽然信息增益大，但其实和样本的划分关系不大（泛化能力弱）。因此引入信息增益率（信息增益 / 划分前的熵值）。

CART分类使用基尼指数（Gini）来选择最好的数据分割的特征，Gini描述的是纯度，与信息熵的含义相似。Gini系数 \(Gini(p)=\sum_{k=1}^Kp_k(1-p_k)=1-\sum_{k=1}^Kp^2\) （同熵一样，值较小时分类效果好）。

引入评价函数：\(C(T)=\sum_{t\in leaf}N_t*H(t)\) ，\(H(t)\)表示熵值或Gini系数值，\(N_t\)表示叶节点中的样本数 （评价函数值越小越好）。

###其他

如何处理连续型的属性：离散化，将连续型属性的值分为不同的区间，依据是比较各个分裂点得到Gain值的大小。

缺失数据的考虑：忽略，即在计算增益时仅考虑那些具有属性值的记录。

当决策树太高、分支太多时很容易过拟合（在训练集上划分为100% 但在测试集上效果不好），于是引入剪枝操作：

• 预剪枝：在构建决策树的过程中，提前停止。如限制深度、限制当前集合的样本个数的最低阈值。
• 后剪枝：在决策树构建好后才开始剪枝。如重新定义评价函数 \(C_\alpha(T)=C(T)+\alpha\cdot\mid T_{leaf}\mid\)（限制叶子节点个数，手动设置\(\alpha\)以控制影响程度），在建树完成之后对每个节点比较剪枝和不剪枝的效果。

##随机森林

随机森林就是通过集成学习的思想将多棵树集成的一种算法，它的基本单元是决策树，本质是一种集成学习（Ensemble Learning）方法。

从直观角度来解释，每棵决策树都是一个分类器，那么对于一个输入样本，N棵树会有N个分类结果。而随机森林集成了所有的分类投票结果，将投票次数最多的类别指定为最终的输出，这就是一种最简单的 Bagging 思想。

随机森林体现了两方面的随机：

• 样本随机 不使用全部数据集，而是随机放回采样（有一定概率避免选到异常点，使得树的效果更好）
• 特征随机 不使用全部特征，而是随机选取一部分特征（有一定概率避开使用传统信息增益出问题的特征）

详细可参看 [Machine Learning & Algorithm] 随机森林（Random Forest）

##sklearn库中的决策树算法

使用sklearn自带的决策树方法简单代码如下：

    from sklearn import tree

    mode = tree.DecisionTreeClassifier(criterion='gini')

    mode.fit(X,Y)
    y_test = mode.predict(x_test)

参数解释：

1.criterion gini or entropy 选择基尼系数或熵值作为评判标准

2.splitter best or random 在连续的特征中需要做切分 前者是在所有特征中找最好的切分点 后者是在部分特征中（数据量大的时候）

3.max_features None（所有），log2，sqrt，N 当候选特征较多时需要作出选择 特征小于50的时候一般使用所有的

4.max_depth 指定最大深度（预剪枝时使用） 数据少或者特征少的时候可以不管这个值，如果模型样本量多，特征也多的情况下，可以尝试限制下

5.min_samples_split 如果某节点的样本数少于min_samples_split，则不会继续再尝试选择最优特征来进行划分如果样本量不大，不需要管这个值。如果样本量数量级非常大，则推荐增大这个值。（预剪枝时使用）

6.min_samples_leaf 这个值限制了叶子节点最少的样本数，如果某叶子节点数目小于样本数，则会和兄弟节点一起被剪枝，如果样本量不大，不需要管这个值，大些如10W可是尝试下5

7.min_weight_fraction_leaf 这个值限制了叶子节点所有样本权重和的最小值，如果小于这个值，则会和兄弟节点一起被剪枝默认是0，就是不考虑权重问题。一般来说，如果有较多样本有缺失值，或者分类树样本的分布类别偏差很大，就会引入样本权重

8.max_leaf_nodes 通过限制最大叶子节点数，可以防止过拟合，默认是"None”，即不限制最大的叶子节点数。如果加了限制，算法会建立在最大叶子节点数内最优的决策树。如果特征不多，可以不考虑这个值，但是如果特征分成多的话，可以加以限制具体的值可以通过交叉验证得到。

9.class_weight 指定样本各类别的的权重，主要是为了防止训练集某些类别的样本过多导致训练的决策树过于偏向这些类别。这里可以自己指定各个样本的权重如果使用“balanced”，则算法会自己计算权重，样本量少的类别所对应的样本权重会高。

10.min_impurity_split 这个值限制了决策树的增长，如果某节点的不纯度(基尼系数，信息增益，均方差，绝对差)小于这个阈值则该节点不再生成子节点。即为叶子节点 。