第四章 PCA降维
目录
1. PCA降维
PCA:主成分分析(Principe conponents Analysis)
2. 维度的概念
一般认为时间的一维,而空间的维度,众说纷纭。霍金认为空间是10维的。
3. 为什么要进行降维?
维度灾难:当维度超过一定值的时候,分类器效果呈现明显下降。
PCA旨在找到数据中的主成分,并利用这些主成分表征原始数据,从而达到降维的目的。举一个简单的例子,在三维空间中有一系列数据点,这些点分布在一个过原点的平面上。如果我们用自然坐标系x,y,z三个轴来表示数据,就需要使用三个维度。而实际上,这些点只出现在一个二维平面上,如果我们通过坐标系旋转变换使得数据所在平面与x,y平面重合,那么我们就可以通过x,y两个维度表达原始数据,并且没有任何损失,这样就完成了数据的降维。而x,y两个轴所包含的信息就是我们要找到的主成分。
4. 目标
提取最有价值的信息(基于方差)
5. 降维后的数据的意义?
降维后物理意义变得模糊,但是不影响我们去后续做分类、预测等的结果。
6. PCA推导过程

7. 结论
- 我们要找最大的方差也就是协方差矩阵最大的特征值;
- 最佳投影方向就是最大特征值对应的特征向量
- 次佳投影方向位于最佳投影方向的正交空间中,是第二大特征值对应的特征向量
求解步骤:
- 对样本数据进行中心化处理
- 求协方差矩阵
- 对协方差矩阵进行特征值分解,将特征值从到小排列
- 取特征值前d大对应的特征向量w1, w2, ..., wd。通过映射关系将n维样本映射到d维空间。
降维后的信息占比定义为:
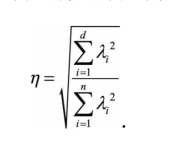
第四章 PCA降维的更多相关文章
- 第十四章:降维:奇异值分解SVD
- 机器学习实战基础(二十三):sklearn中的降维算法PCA和SVD(四) PCA与SVD 之 PCA中的SVD
PCA中的SVD 1 PCA中的SVD哪里来? 细心的小伙伴可能注意到了,svd_solver是奇异值分解器的意思,为什么PCA算法下面会有有关奇异值分解的参数?不是两种算法么?我们之前曾经提到过,P ...
- PRML读书会第四章 Linear Models for Classification(贝叶斯marginalization、Fisher线性判别、感知机、概率生成和判别模型、逻辑回归)
主讲人 planktonli planktonli(1027753147) 19:52:28 现在我们就开始讲第四章,第四章的内容是关于 线性分类模型,主要内容有四点:1) Fisher准则的分类,以 ...
- 《机器学习实战》学习笔记第十四章 —— 利用SVD简化数据
相关博客: 吴恩达机器学习笔记(八) —— 降维与主成分分析法(PCA) <机器学习实战>学习笔记第十三章 —— 利用PCA来简化数据 奇异值分解(SVD)原理与在降维中的应用 机器学习( ...
- R in action读书笔记(19)第十四章 主成分和因子分析
第十四章:主成分和因子分析 本章内容 主成分分析 探索性因子分析 其他潜变量模型 主成分分析(PCA)是一种数据降维技巧,它能将大量相关变量转化为一组很少的不相关变量,这些无关变量称为主成分.探索性因 ...
- 【机器学习】--主成分分析PCA降维从初识到应用
一.前述 主成分分析(Principal Component Analysis,PCA), 是一种统计方法.通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分. ...
- Python机器学习笔记 使用scikit-learn工具进行PCA降维
之前总结过关于PCA的知识:深入学习主成分分析(PCA)算法原理.这里打算再写一篇笔记,总结一下如何使用scikit-learn工具来进行PCA降维. 在数据处理中,经常会遇到特征维度比样本数量多得多 ...
- PCA降维笔记
PCA降维笔记 一个非监督的机器学习算法 主要用于数据的降维 通过降维, 可以发现更便 于人类理解的特征 其他应用:可视化:去噪 PCA(Principal Component Analysis)是一 ...
- sklearn pca降维
PCA降维 一.原理 这篇文章总结的不错PCA的数学原理. PCA主成分分析是将原始数据以线性形式映射到维度互不相关的子空间.主要就是寻找方差最大的不相关维度.数据的最大方差给出了数据的最重要信息. ...
随机推荐
- c语言spline
#define NRANSI #include "nrutil.h" void spline(float x[], float y[], int n, float yp1, flo ...
- 根据方法名获取方法Body Content
利用 MethodBody类的GetILAsByteArray方法可以获取到返回字节数组的MSIL的body.然后再去解析此字节数组, 可以得到MSIL,然后你再去解析MSIL,你就可以得到你想到so ...
- AngularJS 无限滚动加载数据控件 ngInfiniteScroll
在开发中我们可能会遇到滚动鼠标到浏览器底部实现数据的加载,js和jquery实现都不复杂都是既然AngularJS提供现成的我们怎么不用昵. ng-infinite-scroll.js这个组件则可以实 ...
- C#-ado.net学习笔记-会有更新
ado.net 通用类对象.在本地内存暂存数据 托管类对象.让本地通用类对象连接数据库,让本地通用类对象和数据库同步 连接数据库 new connection(connectstring) comma ...
- C#-VS程序集
程序集即代码组,可以是单个文件或多个文件,按一个整体部署,但可指定自身调用其他程序集的版本. 推出原因 为解决dll地狱而推出,也可解决其他问题.dll地狱,a应用使用dll版本1,b应用使用dll版 ...
- shell脚本-成长之路
我对shell脚本的认识,除了执行过同事写的shell 脚本外,其他一无所知,为了让自己强大,我决定自己研究shell脚本,也许在你看来很简答,没必要说这么多废话,但是我希望在我的技术log里记录下来 ...
- SSM_CRUD新手练习(2)配置文件
配置之前现需要引入依赖的jar包: *Spring *SpringMvc *Mybatis *数据库连接池,驱动包 *其他(jstl,Servlet ,Junit..) 1.poxm.xml < ...
- PAT甲级 1130. Infix Expression (25)
1130. Infix Expression (25) 时间限制 400 ms 内存限制 65536 kB 代码长度限制 16000 B 判题程序 Standard 作者 CHEN, Yue Give ...
- 关于QT建立项目中遇到的相关问题的处理办法
关于QT建立项目中遇到的相关问题的处理办法 1.在QTCreater中新建一个空的工程时,第一次运行会抱一个错误,如下: -1: error: LNK1123: 转换到 COFF 期间失败: 文件无效 ...
- hdu 4704 Sum 【费马小定理】
题目 题意:将N拆分成1-n个数,问有多少种组成方法. 例如:N=4,将N拆分成1个数,结果就是4:将N拆分成2个数,结果就是3(即:1+3,2+2,3+1)--1+3和3+1这个算两个,则这个就是组 ...
