P1251 餐巾计划 (网络流)

题意:餐厅每天会需要用Ri块新的餐巾 用完后也会产生Ri块旧的餐巾

　　 每天购买新的餐巾单价p元 每天产出的旧餐巾可以送到快洗部花费每张c1元 在i + v1天可以使用

　　 也可以花费c2元每张送到慢洗部 在i + v2天可以使用 问n天的最小花费

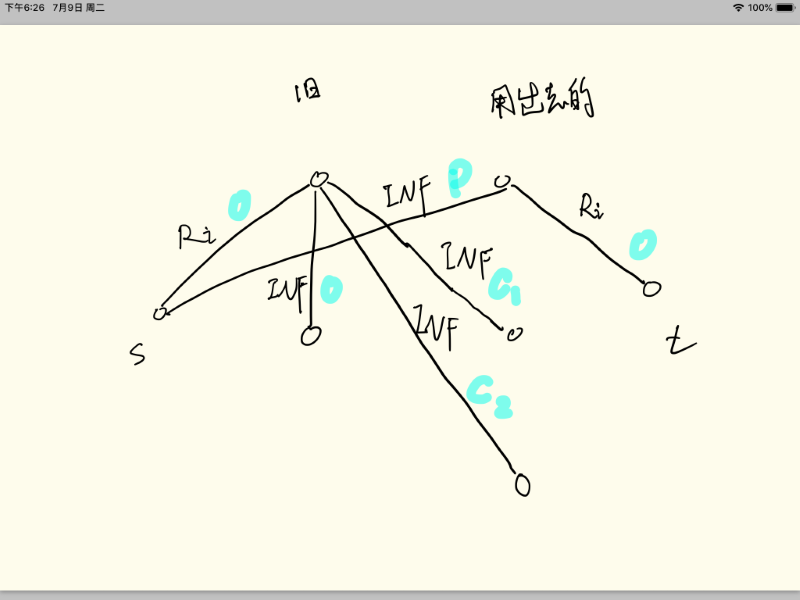
题解:把每天拆点 分为用出去的 和得到的旧餐巾

　　 s -> 用出去的  表示每天可以买新的

　　 用出去的-> t 表示每天一定会用Ri张纸巾

　　 s-> 旧 表示每天一定会产生Ri块旧的纸巾

　　 特判一下后 旧的按题意可以送去快洗和慢洗 然后今天没用完的旧的 明天也可以用

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;

int n, v1, c1, v2, c2, p;
int cnt, s, t;
int q[2005];
ll mincost, maxflow;

struct node {
    int to, nex, val, cost;
}E[25005];
int head[4005];
int cur[4005];

void addedge(int x, int y, int va, int cos) {
    E[++cnt].to = y; E[cnt].nex = head[x]; head[x] = cnt; E[cnt].val = va; E[cnt].cost = cos;
    E[++cnt].to = x; E[cnt].nex = head[y]; head[y] = cnt; E[cnt].val = 0; E[cnt].cost = -cos;
}

int inque[4005];
int dis[4005];
int vis[4005];
bool spfa() {
    for(int i = 0; i <= (n << 1 | 1); i++) dis[i] = INF, inque[i] = 0, cur[i] = head[i], vis[i] = 0;
    queue<int> que;
    que.push(s);
    dis[s] = 0;
    inque[s] = 1;

    while(!que.empty()) {
        int u = que.front();
        que.pop();
        inque[u] = 0;

        for(int i = head[u]; i; i = E[i].nex) {
            int v = E[i].to;
            if(E[i].val > 0 && dis[v] > dis[u] + E[i].cost) {
                dis[v] = dis[u] + E[i].cost;
                if(!inque[v]) {
                    que.push(v);
                    inque[v] = 1;
                }
            }
        }
    }
    if(dis[t] != INF) return true;
    return false;
}

int dfs(int x, int flow) {
    if(x == t) {
        vis[t] = 1;
        return flow;
    }

    vis[x] = 1;
    int used = 0;
    int rflow = 0;
    for(int i = cur[x]; i; i = E[i].nex) {
        cur[x] = i;
        int v = E[i].to;
        if(E[i].val > 0 && dis[v] == dis[x] + E[i].cost && (!vis[v] || v == t)) {
            if(rflow = dfs(v, min(flow - used, E[i].val))) {
                used += rflow;
                E[i].val -= rflow;
                E[i ^ 1].val += rflow;
                mincost += 1LL * rflow * E[i].cost;
                if(used == flow) break;
            }
        }
    }
    return used;
}

void dinic() {
    while(spfa()) {
        vis[t] = 1;
        while(vis[t]) {
            vis[t] = 0;
            dfs(s, INF);
        }
    }
}

int main() {
    mincost = maxflow = 0;
    cnt = 1;
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) scanf("%d", &q[i]), maxflow += 1LL * q[i];
    s = 0; t = 1;
    scanf("%d%d%d%d%d", &p, &v1, &c1, &v2, &c2);

    for(int i = 1; i <= n; i++) {
        addedge(s, i << 1, q[i], 0);
        addedge(i << 1 | 1, t, q[i], 0);
        addedge(s, i << 1 | 1, INF, p);
        if(i + v1 <= n) addedge(i << 1, (i + v1) << 1 | 1, INF, c1);
        if(i + v2 <= n) addedge(i << 1, (i + v2) << 1 | 1, INF, c2);
        if(i + 1 <= n) addedge(i << 1, (i + 1) << 1, INF, 0);
    }
    dinic();
    printf("%lld\n", mincost);
    return 0;
}