Arrays.sort() ----- TimSort

Arrays.sort()

Arrays.sort()对于基本类型使用的是DualPivotQuicksort双轴快速排序，而对于非基本类型使用的是TimSort，一种源自合并排序和插入排序的混合稳定算法。

算法

1. 划分run

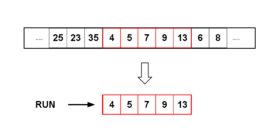
   1. 找出数组中按升序排序的区域（arr[i]<=arr[i+1]）或者按严格降序排序的区域(arr[i]>arr[i+1]),这块区域就叫run。

   2. 翻转严格降序的区域，严格降序就是为了这步不破坏稳定性。

   3. run长度如果小于minRun，将binarySort扩展到minRun。
      
      minRun，每块run的最小长度。定义引用wiki上的一段话：

      Because merging is most efficient when the number of runs is equal to, or slightly less than, a power of two, and notably less efficient when the number of runs is slightly more than a power of two, Timsort chooses minrun to try to ensure the former condition.

      大意是说合并只有在run的个数在等于或者稍小于2^n才最有效，TimSort用minRun来保证。
      
      

2. 压栈
   
   栈保存run的起始位置和长度

3. 合并
   
   合并是为了是合并的run长度达到接近。
   
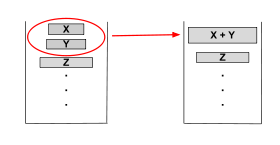
   为了追求平衡的合并，Timsort考虑了堆栈顶部的三个run，X，Y，Z，并维护不变量：
   
   1.| Z | > | Y | + | X |
   
   2.| Y | > | X |
   
   如果违反了不变量，则Y与X或Z中的较小者合并，并再次检查不变量。
   
   

4. 重复以上步骤直到数组都划分完成

5. 合并栈上剩下的run

jdk1.8源码

static <T> void sort(T[] a, int lo, int hi, Comparator<? super T> c,
                     T[] work, int workBase, int workLen) {
    assert c != null && a != null && lo >= 0 && lo <= hi && hi <= a.length;

    int nRemaining  = hi - lo;
    if (nRemaining < 2)
        return;

	//数组长度小于32，直接用二分插入排序
    if (nRemaining < MIN_MERGE) {
        int initRunLen = countRunAndMakeAscending(a, lo, hi, c);
        binarySort(a, lo, hi, lo + initRunLen, c);
        return;
    }

    TimSort<T> ts = new TimSort<>(a, c, work, workBase, workLen);
	//计算minRun
    int minRun = minRunLength(nRemaining);
    do {
        //1.1-1.2 获取run的长度，并翻转严格降序run
        int runLen = countRunAndMakeAscending(a, lo, hi, c);

        //1.3 如果长度小于minRun，扩展run
        if (runLen < minRun) {
            int force = nRemaining <= minRun ? nRemaining : minRun;
            binarySort(a, lo, lo + force, lo + runLen, c);
            runLen = force;
        }

        //2. 压栈
        ts.pushRun(lo, runLen);
		//3. 合并run
        ts.mergeCollapse();

        // Advance to find next run
        lo += runLen;
        nRemaining -= runLen;
    } while (nRemaining != 0);//4.重复步骤1-3

    //5.合并剩下的run
    assert lo == hi;
    ts.mergeForceCollapse();
    assert ts.stackSize == 1;
}

countRunAndMakeAscending 获取run的长度并翻转严格降序run

private static <T> int countRunAndMakeAscending(T[] a, int lo, int hi,
                                                Comparator<? super T> c) {
    assert lo < hi;
    int runHi = lo + 1;
    if (runHi == hi)
        return 1;

    // Find end of run, and reverse range if descending
    if (c.compare(a[runHi++], a[lo]) < 0) { // Descending
        while (runHi < hi && c.compare(a[runHi], a[runHi - 1]) < 0)
            runHi++;
        reverseRange(a, lo, runHi);
    } else {                              // Ascending
        while (runHi < hi && c.compare(a[runHi], a[runHi - 1]) >= 0)
            runHi++;
    }

    return runHi - lo;
}

binarySort 二分插入排序

private static <T> void binarySort(T[] a, int lo, int hi, int start,
                                   Comparator<? super T> c) {
    assert lo <= start && start <= hi;
    if (start == lo)
        start++;
    for ( ; start < hi; start++) {
        T pivot = a[start];

        // Set left (and right) to the index where a[start] (pivot) belongs
        int left = lo;
        int right = start;
        assert left <= right;
        /*
         * Invariants:
         *   pivot >= all in [lo, left).
         *   pivot <  all in [right, start).
         */
        while (left < right) {
            int mid = (left + right) >>> 1;
            if (c.compare(pivot, a[mid]) < 0)
                right = mid;
            else
                left = mid + 1;
        }
        assert left == right;

        /*
         * The invariants still hold: pivot >= all in [lo, left) and
         * pivot < all in [left, start), so pivot belongs at left.  Note
         * that if there are elements equal to pivot, left points to the
         * first slot after them -- that's why this sort is stable.
         * Slide elements over to make room for pivot.
         */
        int n = start - left;  // The number of elements to move
        // Switch is just an optimization for arraycopy in default case
        switch (n) {
            case 2:  a[left + 2] = a[left + 1];
            case 1:  a[left + 1] = a[left];
                     break;
            default: System.arraycopy(a, left, a, left + 1, n);
        }
        a[left] = pivot;
    }
}

minRunLength 计算minRun

如果数组长度为2^n，minRun为16（MIN_MERGE/2）；

否则取长度的高4位，奇数补1，MIN_MERGE/2<=minRun<MIN_MERGE。

private static int minRunLength(int n) {
    assert n >= 0;
    int r = 0;      // Becomes 1 if any 1 bits are shifted off
    while (n >= MIN_MERGE) {
        r |= (n & 1);
        n >>= 1;
    }
    return n + r;
}

pushRun 压栈

runBase存run的起始位置

runLen存run的长度

runBase[i]+runLen[i]=runBase[i+1]

private void pushRun(int runBase, int runLen) {
    this.runBase[stackSize] = runBase;
    this.runLen[stackSize] = runLen;
    stackSize++;
}

mergeCollapse 合并

//判断数组尾部，即刚入栈的三个run是否符合上述的不变量。不满足即合并。
private void mergeCollapse() {
    while (stackSize > 1) {
        int n = stackSize - 2;
        if (n > 0 && runLen[n-1] <= runLen[n] + runLen[n+1]) {
            if (runLen[n - 1] < runLen[n + 1])
                n--;
            mergeAt(n);
        } else if (runLen[n] <= runLen[n + 1]) {
            mergeAt(n);
        } else {
            break; // Invariant is established
        }
    }
}

合并时相对归并排序做了很多优化，如:

1.先找出第二个数组第一个元素在第一个数组中的位置，小于这个位置的不用排序，直接合并；

2.再找出第一个数组最后一个元素再第二个数组中的位置，大于这个位置的不用排序，直接合并；

3.查找位置会用到Galloping mode

private void mergeAt(int i) {
    assert stackSize >= 2;
    assert i >= 0;
    assert i == stackSize - 2 || i == stackSize - 3;

    int base1 = runBase[i];
    int len1 = runLen[i];
    int base2 = runBase[i + 1];
    int len2 = runLen[i + 1];
    assert len1 > 0 && len2 > 0;
    assert base1 + len1 == base2;

    //如果合并的是数组倒数第二和第三个run，将最后一个向前移动
    runLen[i] = len1 + len2;
    if (i == stackSize - 3) {
        runBase[i + 1] = runBase[i + 2];
        runLen[i + 1] = runLen[i + 2];
    }
    stackSize--;

    //1.先找出第二个数组第一个元素在第一个数组中的位置，小于这个位置的不用排序
    int k = gallopRight(a[base2], a, base1, len1, 0, c);
    assert k >= 0;
    base1 += k;
    len1 -= k;
    if (len1 == 0)
        return;

    //2. 再找出第一个数组最后一个元素再第二个数组中的位置，大于这个位置的不用排序
    len2 = gallopLeft(a[base1 + len1 - 1], a, base2, len2, len2 - 1, c);
    assert len2 >= 0;
    if (len2 == 0)
        return;

    // Merge remaining runs, using tmp array with min(len1, len2) elements
    if (len1 <= len2)
        mergeLo(base1, len1, base2, len2);
    else
        mergeHi(base1, len1, base2, len2);
}

Galloping mode

1.先找到arr[i(n-1)]<key<=arr[i(n)],i(n)=2^n+1。即比较key与第1，3，5，7...个数据。

2.再在i(n-1)~i(n)的范围内二分查找key。

private static <T> int gallopLeft(T key, T[] a, int base, int len, int hint,
                                  Comparator<? super T> c) {
    assert len > 0 && hint >= 0 && hint < len;
    int lastOfs = 0;
    int ofs = 1;
    if (c.compare(key, a[base + hint]) > 0) {
        // Gallop right until a[base+hint+lastOfs] < key <= a[base+hint+ofs]
        int maxOfs = len - hint;
        while (ofs < maxOfs && c.compare(key, a[base + hint + ofs]) > 0) {
            lastOfs = ofs;
            ofs = (ofs << 1) + 1;
            if (ofs <= 0)   // int overflow
                ofs = maxOfs;
        }
        if (ofs > maxOfs)
            ofs = maxOfs;

        // Make offsets relative to base
        lastOfs += hint;
        ofs += hint;
    } else { // key <= a[base + hint]
        // Gallop left until a[base+hint-ofs] < key <= a[base+hint-lastOfs]
        final int maxOfs = hint + 1;
        while (ofs < maxOfs && c.compare(key, a[base + hint - ofs]) <= 0) {
            lastOfs = ofs;
            ofs = (ofs << 1) + 1;
            if (ofs <= 0)   // int overflow
                ofs = maxOfs;
        }
        if (ofs > maxOfs)
            ofs = maxOfs;

        // Make offsets relative to base
        int tmp = lastOfs;
        lastOfs = hint - ofs;
        ofs = hint - tmp;
    }
    assert -1 <= lastOfs && lastOfs < ofs && ofs <= len;

    /*
     * Now a[base+lastOfs] < key <= a[base+ofs], so key belongs somewhere
     * to the right of lastOfs but no farther right than ofs.  Do a binary
     * search, with invariant a[base + lastOfs - 1] < key <= a[base + ofs].
     */
    lastOfs++;
    while (lastOfs < ofs) {
        int m = lastOfs + ((ofs - lastOfs) >>> 1);

        if (c.compare(key, a[base + m]) > 0)
            lastOfs = m + 1;  // a[base + m] < key
        else
            ofs = m;          // key <= a[base + m]
    }
    assert lastOfs == ofs;    // so a[base + ofs - 1] < key <= a[base + ofs]
    return ofs;
}

真正合并数组也会用到Galloping mode，当一个数组连续小于某个数的次数达到一定阈值，会切换为Galloping mode，找到连续小于这个值的数量。

private void mergeLo(int base1, int len1, int base2, int len2) {
    assert len1 > 0 && len2 > 0 && base1 + len1 == base2;

    // Copy first run into temp array
    T[] a = this.a; // For performance
    T[] tmp = ensureCapacity(len1);
    int cursor1 = tmpBase; // Indexes into tmp array
    int cursor2 = base2;   // Indexes int a
    int dest = base1;      // Indexes int a
	//将较小的数组放入临时数组
    System.arraycopy(a, base1, tmp, cursor1, len1);

    // Move first element of second run and deal with degenerate cases
    a[dest++] = a[cursor2++];
    if (--len2 == 0) {
        System.arraycopy(tmp, cursor1, a, dest, len1);
        return;
    }
    if (len1 == 1) {
        System.arraycopy(a, cursor2, a, dest, len2);
        a[dest + len2] = tmp[cursor1]; // Last elt of run 1 to end of merge
        return;
    }

    Comparator<? super T> c = this.c;  // Use local variable for performance
    //出现多少次连续事件切换到Galloping mode的阈值
	int minGallop = this.minGallop;    //  "    "       "     "      "
outer:
    while (true) {
        int count1 = 0; // 连续第一个run小于第二个run的次数
        int count2 = 0; // 连续第二个run小于第一个run的次数

        //用顺序插入排序
        do {
            assert len1 > 1 && len2 > 0;
            if (c.compare(a[cursor2], tmp[cursor1]) < 0) {
                a[dest++] = a[cursor2++];
                count2++;
                count1 = 0;
                if (--len2 == 0)
                    break outer;
            } else {
                a[dest++] = tmp[cursor1++];
                count1++;
                count2 = 0;
                if (--len1 == 1)
                    break outer;
            }
        } while ((count1 | count2) < minGallop);//达到阈值，切换到Galloping mode

        //达到阈值后，用Galloping mode获取到小于该值的个数，减少copy次数
        do {
            assert len1 > 1 && len2 > 0;
            count1 = gallopRight(a[cursor2], tmp, cursor1, len1, 0, c);
            if (count1 != 0) {
                System.arraycopy(tmp, cursor1, a, dest, count1);
                dest += count1;
                cursor1 += count1;
                len1 -= count1;
                if (len1 <= 1) // len1 == 1 || len1 == 0
                    break outer;
            }
            a[dest++] = a[cursor2++];
            if (--len2 == 0)
                break outer;

            count2 = gallopLeft(tmp[cursor1], a, cursor2, len2, 0, c);
            if (count2 != 0) {
                System.arraycopy(a, cursor2, a, dest, count2);
                dest += count2;
                cursor2 += count2;
                len2 -= count2;
                if (len2 == 0)
                    break outer;
            }
            a[dest++] = tmp[cursor1++];
            if (--len1 == 1)
                break outer;
            minGallop--;
        } while (count1 >= MIN_GALLOP | count2 >= MIN_GALLOP);
        if (minGallop < 0)
            minGallop = 0;
        minGallop += 2;  // Penalize for leaving gallop mode
    }  // End of "outer" loop
    this.minGallop = minGallop < 1 ? 1 : minGallop;  // Write back to field

    if (len1 == 1) {
        assert len2 > 0;
        System.arraycopy(a, cursor2, a, dest, len2);
        a[dest + len2] = tmp[cursor1]; //  Last elt of run 1 to end of merge
    } else if (len1 == 0) {
        throw new IllegalArgumentException(
            "Comparison method violates its general contract!");
    } else {
        assert len2 == 0;
        assert len1 > 1;
        System.arraycopy(tmp, cursor1, a, dest, len1);
    }
}

时间复杂度和空间复杂度

在部分排序的数组上运行时，需要远远少于n lg（n）的比较，同时在随机数组上运行时性能堪比传统的mergesort。像所有合并排序一样，这种类型是稳定的，并运行O（n log n）时间（最坏情况）。在最坏的情况下，这种类型需要临时存储空间来存放n / 2个对象引用; 在最好的情况下，它只需要很小的恒定空间。

参考资料

https://en.wikipedia.org/wiki/Timsort#cite_note-python_timsort-8

https://www.jianshu.com/p/10aa41b780f2