机器学习实战---决策树CART简介及分类树实现
https://www.cnblogs.com/pinard/p/6053344.html
一:CART算法简介
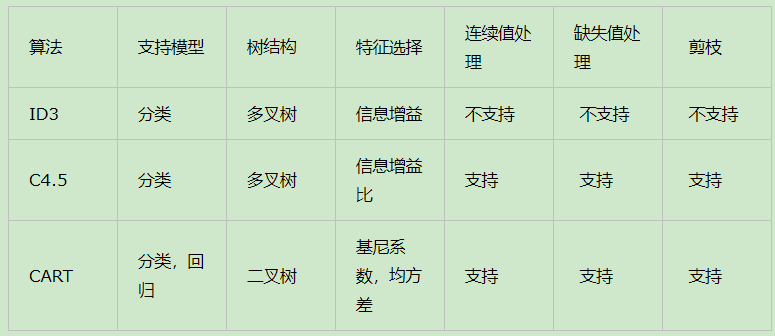
(一)CART、ID3、C4.5比较
CART算法的全称是Classification And Regression Tree,采用的是Gini指数(选Gini指数最小的特征s)作为分裂标准,同时它也是包含后剪枝操作。
ID3算法和C4.5算法虽然在对训练样本集的学习中可以尽可能多地挖掘信息,但其生成的决策树分支较大,规模较大。
为了简化决策树的规模,提高生成决策树的效率,就出现了根据GINI系数来选择测试属性的决策树算法CART。
(二)CART分类与回归
CART分类与回归树本质上是一样的,构建过程都是逐步分割特征空间,预测过程都是从根节点开始一层一层的判断直到叶节点给出预测结果。
只不过分类树给出离散值,而回归树给出连续值(通常是叶节点包含样本的均值),
另外分类树基于Gini指数选取分割点,而回归树基于平方误差选取分割点。
(三)基尼指数
1.ID3、C4.5
在ID3算法中我们使用了信息增益来选择特征,信息增益大的优先选择。在C4.5算法中,采用了信息增益比来选择特征,以减少信息增益容易选择特征值多的特征的问题。但是无论是ID3还是C4.5,都是基于信息论的熵模型的,这里面会涉及大量的对数运算。
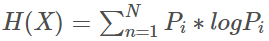
2.能不能简化模型同时也不至于完全丢失熵模型的优点呢?
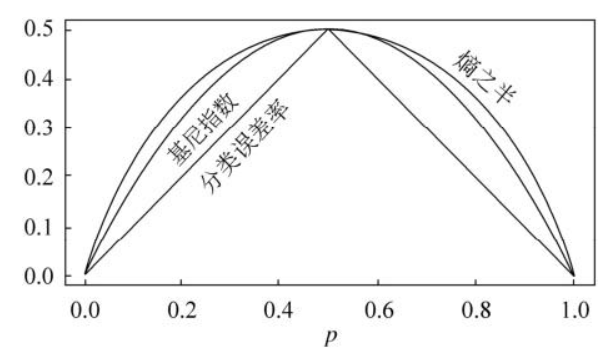
CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。
3.基尼指数定义
假设有数据集 ,且
有
个分类,那么可定义基尼指数为:
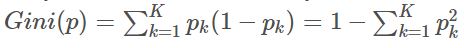
从公式可以看到,基尼指数的意义是:从数据集D中随机抽取两个样本,其类别不同的概率。直觉地,基尼指数越小,则数据集D的纯度越高。
如果训练数据集D根据特征A是否取某一可能值a被分割为D1和D2两部分,则在特征A的条件下,集合D的基尼指数定义为:
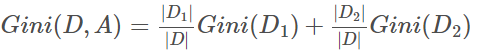
基尼指数Gini(D)表示集合D的不确定性,基尼指数Gini(D,A)表示经过A=a分割后集合D的不确定性。基尼指数越大,样本的不确定性也就越大。
相对于用信息增益/信息增益率来作为决策指标(含log操作),基尼指数的运算量比较小,也很易于理解,这是cart算法使用基尼指数的主要目的。
二:CART分类树算法对于连续特征和离散特征处理的改进
(一)连续特征
对于CART分类树连续值的处理问题,其思想和C4.5是相同的,都是将连续的特征离散化。
唯一的区别在于在选择划分点时的度量方式不同,C4.5使用的是信息增益比,则CART分类树使用的是基尼系数。
具体的思路如下,比如m个样本的连续特征A有m个,从小到大排列为a1,a2,...,am,则CART算法取相邻两样本值的平均数,一共取得m-1个划分点。
其中第i个划分点Ti表示为:Ti=(ai+ai+1)/2。
对于这m-1个点,分别计算以该点作为二元分类点时的基尼系数。
选择基尼系数最小的点作为该连续特征的二元离散分类点。
比如取到的基尼系数最小的点为at,则小于at的值为类别1,大于at的值为类别2,这样我们就做到了连续特征的离散化。
要注意的是,与ID3或者C4.5处理离散属性不同的是,如果当前节点为连续属性,则该属性后面还可以参与子节点的产生选择过程。
(二)离散值
对于CART分类树离散值的处理问题,采用的思路是不停的二分离散特征。
回忆下ID3或者C4.5,如果某个特征A被选取建立决策树节点,如果它有A1,A2,A3三种类别,我们会在决策树上一下建立一个三叉的节点。这样导致决策树是多叉树。但是CART分类树使用的方法不同,他采用的是不停的二分。
还是这个例子,CART分类树会考虑把A分成{A1}和{A2,A3}, {A2}和{A1,A3}, {A3}和{A1,A2}三种情况,找到基尼系数最小的组合,比如{A2}和{A1,A3},然后建立二叉树节点,一个节点是A2对应的样本,另一个节点是{A1,A3}对应的节点。
同时,由于这次没有把特征A的取值完全分开,后面我们还有机会在子节点继续选择到特征A来划分A1和A3。这和ID3或者C4.5不同,在ID3或者C4.5的一棵子树中,离散特征只会参与一次节点的建立。
三:分类算法逻辑


四:决策树分类代码实现
https://www.cnblogs.com/ssyfj/p/13229743.html
(一)实现求解基尼指数
import numpy as np def calcGini(data_y): #根据基尼指数的定义,根据当前数据集中不同标签类出现次数,获取当前数据集D的基尼指数
m = data_y.size #获取全部数据数量
labels = np.unique(data_y) #获取所有标签值类别(去重后)
gini = 1.0 #初始基尼系数 for i in labels: #遍历每一个标签值种类
y_cnt = data_y[np.where(data_y==i)].size / m #出现概率
gini -= y_cnt** #基尼指数 return gini
测试:
print(calcGini(np.array([,,,,,,,,])))

(二)实现数据集切分
def splitDataSet(data_X,data_Y,fea_axis,fea_val): #根据特征、和该特征下的特征值种类,实现切分数据集和标签
#根据伪算法可以知道,我们要将数据集划分为2部分:特征值=a和特征值不等于a
eqIdx = np.where(data_X[:,fea_axis]==fea_val)
neqIdx = np.where(data_X[:,fea_axis]!=fea_val) return data_X[eqIdx],data_Y[eqIdx],data_X[neqIdx],data_Y[neqIdx]
(三)实现选取最优特征和特征值划分
def chooseBestFeature(data_X,data_Y): #遍历所有特征和特征值,选取最优划分
m,n = data_X.shape
bestFeature = -
bestFeaVal = -
minFeaGini = np.inf for i in range(n): #遍历所有特征
fea_cls = np.unique(data_X[:,i]) #获取该特征下的所有特征值
# print("{}---".format(fea_cls))
for j in fea_cls: #遍历所有特征值
newEqDataX,newEqDataY,newNeqDataX,newNeqDataY=splitDataSet(data_X,data_Y,i,j) #进行数据集切分 feaGini = #计算基尼指数
feaGini += newEqDataY.size/m*calcGini(newEqDataY) + newNeqDataY.size/m*calcGini(newNeqDataY)
if feaGini < minFeaGini:
bestFeature = i
bestFeaVal = j
minFeaGini = feaGini
return bestFeature,bestFeaVal #返回最优划分方式
(四)创建CART决策树
def createTree(data_X,data_Y,fea_idx): #创建决策树
y_labels = np.unique(data_Y)
#.如果数据集中,所有实例都属于同一类,则返回
if y_labels.size == :
return data_Y[] #.如果特征集为空,表示遍历了所有特征,使用多数投票进行决定
if data_X.shape[] == :
bestFea,bestCnt = ,
for i in y_labels:
cnt = data_Y[np.where(data_Y==i)].size
if cnt > bestCnt:
bestFea = i
bestCnt = cnt
return bestFea #按照基尼指数,选择特征,进行继续递归创建树
bestFeature, bestFeaVal = chooseBestFeature(data_X,data_Y)
# print(bestFeature,bestFeaVal)
feaBestIdx = fea_idx[bestFeature]
my_tree = {feaBestIdx:{}}
#获取划分结果
newEqDataX,newEqDataY,newNeqDataX,newNeqDataY = splitDataSet(data_X,data_Y,bestFeature,bestFeaVal)
#删除我们选择的最优特征
newEqDataX = np.delete(newEqDataX,bestFeature,)
newNeqDataX = np.delete(newNeqDataX,bestFeature,) fea_idx = np.delete(fea_idx,bestFeature,) my_tree[feaBestIdx]["{}_{}".format(,bestFeaVal)] = createTree(newEqDataX,newEqDataY,fea_idx)
my_tree[feaBestIdx]["{}_{}".format(,bestFeaVal)] = createTree(newNeqDataX,newNeqDataY,fea_idx) return my_tree
(五)测试函数
def preDealData(filename):
df = pd.read_table(filename,'\t',header = None)
columns = ["age","prescript","astigmatic","tearRate"] # df.columns = ["age","prescript","astigmatic","tearRate","Result"] #https://zhuanlan.zhihu.com/p/60248460 #数据预处理,变为可以处理的数据 #https://blog.csdn.net/liuweiyuxiang/article/details/78222818
new_df = pd.DataFrame()
for i in range(len(columns)):
new_df[i] = pd.factorize(df[i])[] ##factorize函数可以将Series中的标称型数据映射称为一组数字,相同的标称型映射为相同的数字。
data_X = new_df.values
data_Y = pd.factorize(df[df.shape[]-])[] #factorize返回的是ndarray类型
data_Y = np.array([data_Y]).T return data_X,data_Y,columns data_X,data_Y,fea_names = preDealData("lenses.txt")
fea_Idx = np.arange(len(fea_names)) print(createTree(data_X,data_Y,fea_Idx))
step 1:特征0-特征3
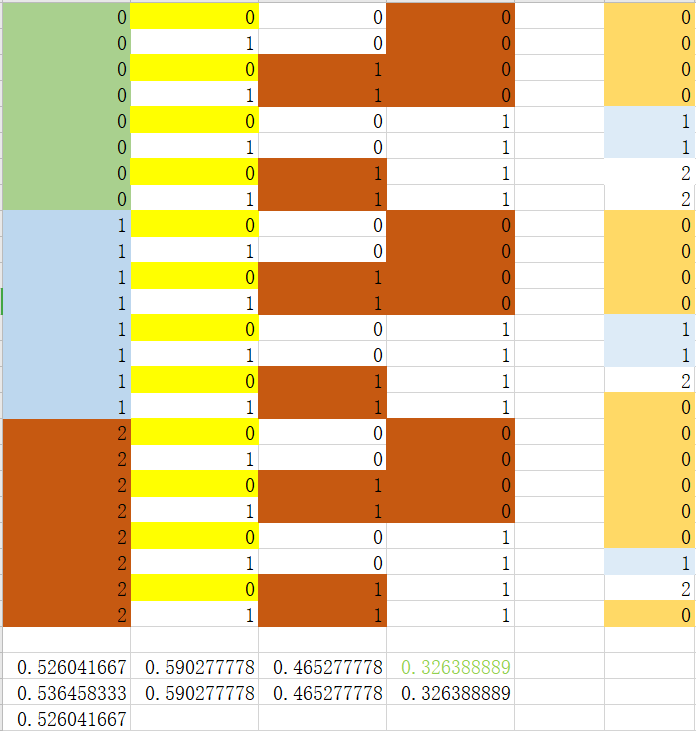
划分后:可以看到选取特征3中特征值为0或者1时,基尼指数值最小,当特征3中特征值为0时,全部是同一类别,所以不再进行下一步处理。后面只处理特征值为1的数据集
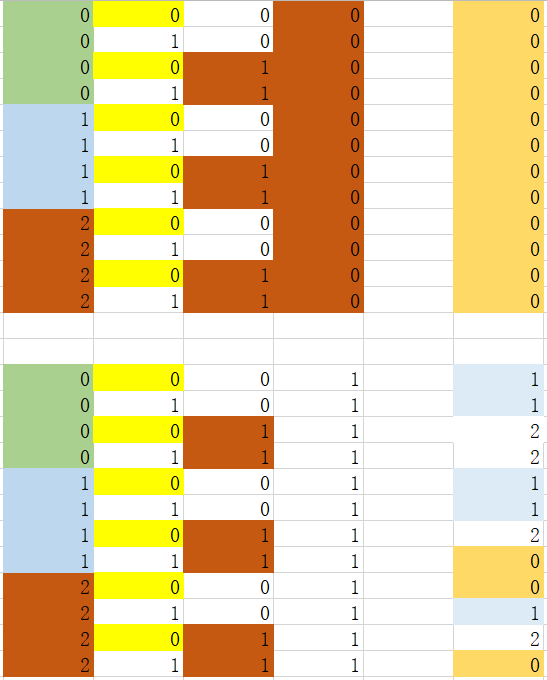
step 2:处理了特征3,还有特征0-特征2
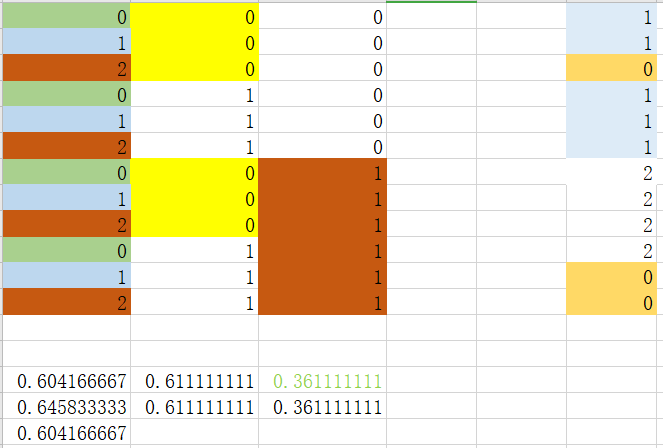
划分后:可以看到选取特征2中的特征值为0或者1时,出现基尼指数值最小。以此为划分依据,分两种情况讨论
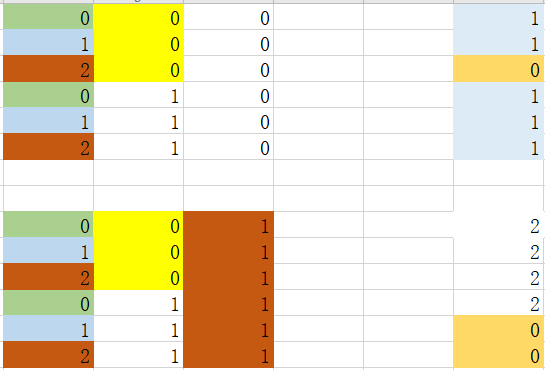
step 3_1:处理特征2中值为0的数据集
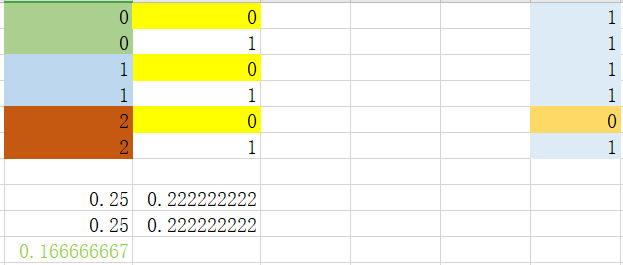
可以看到选取特征0中特征值为2作为最优划分依据,因为基尼指数最小。
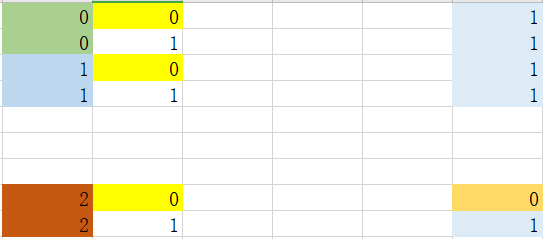
可以看到选取特征值为2时,需要进一步划分。当特征值为非2时(0_2),结果为1,不需要进行下一步处理
step 3_1_1:处理特征0中值为2的数据集

可以看到,对于特征1中的特征值0或者1都是纯净数据,不需要进一步划分。
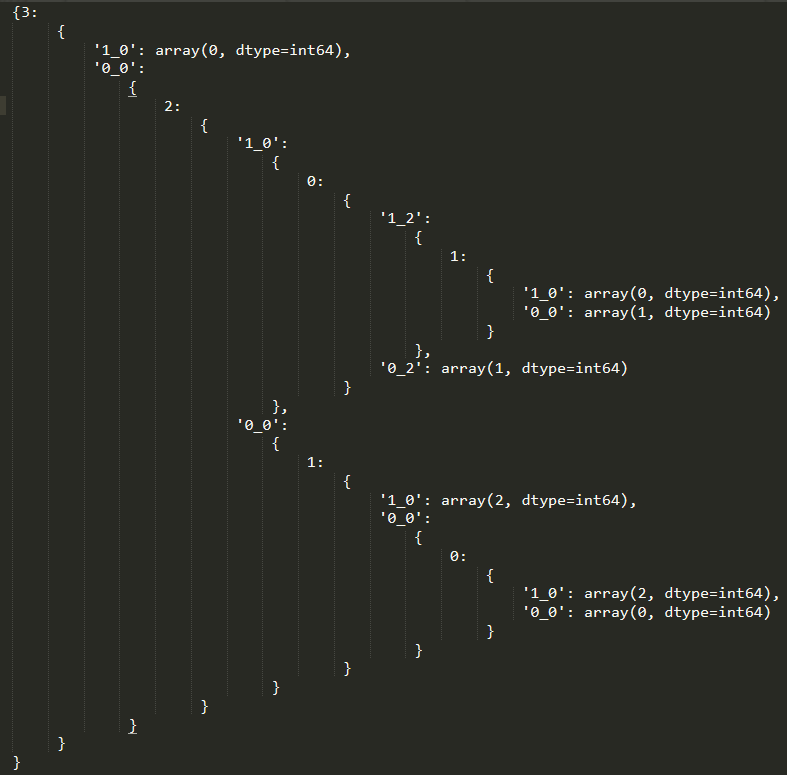
以上推导满足下面决策:

注意:其中x_y表示是否选取特征值y。比如图中1_2,表示选取特征0下,特征值选取2的数据集划分。1_y表示选取这个特征值,0_y表示选取非该特征值下的其他数据集
step 3_2:处理特征2中值为1的数据集

计算基尼指数:
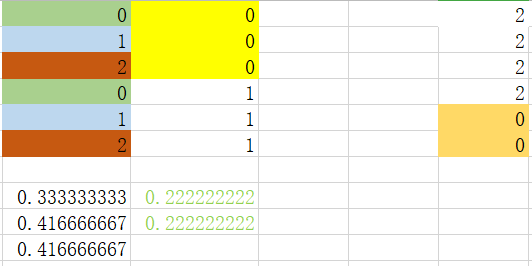
根据最小基尼指数,我们选取特征1中,特征值为0进行划分数据集,由于特征1中特征值为0时数据为纯净数据,不需要进一步划分。对于特征值为1,我们需要进行下一步划分
step 3_2_1:划分特征1中特征值为1 的数据集
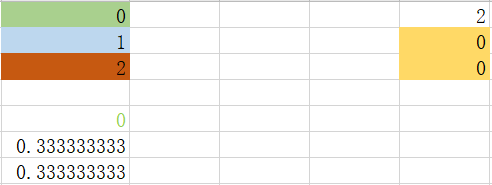
根据最小基尼指数值,我们选取特征0中,特征值为0进行数据集划分。此时特征值为0或者非0情况下,都是纯净数据,不需要下一步划分。于是达到下面情况:
(六)全部代码


import numpy as np
import pandas as pd # 创建数据集
def createDataSet():
dataSet = [[, ],
[, ],
[, ],
[, ],
[, ]]
labels = [, , , , ]
features_names = ['水下', '脚蹼'] # 特征名称 return dataSet, labels, features_names def calcGini(data_y): #根据基尼指数的定义,根据当前数据集中不同标签类出现次数,获取当前数据集D的基尼指数
m = data_y.size #获取全部数据数量
labels = np.unique(data_y) #获取所有标签值类别(去重后)
gini = 1.0 #初始基尼系数 for i in labels: #遍历每一个标签值种类
y_cnt = data_y[np.where(data_y==i)].size / m #出现概率
gini -= y_cnt** #基尼指数 return gini def splitDataSet(data_X,data_Y,fea_axis,fea_val): #根据特征、和该特征下的特征值种类,实现切分数据集和标签
#根据伪算法可以知道,我们要将数据集划分为2部分:特征值=a和特征值不等于a
eqIdx = np.where(data_X[:,fea_axis]==fea_val)
neqIdx = np.where(data_X[:,fea_axis]!=fea_val) return data_X[eqIdx],data_Y[eqIdx],data_X[neqIdx],data_Y[neqIdx] def chooseBestFeature(data_X,data_Y): #遍历所有特征和特征值,选取最优划分
m,n = data_X.shape
bestFeature = -
bestFeaVal = -
minFeaGini = np.inf for i in range(n): #遍历所有特征
fea_cls = np.unique(data_X[:,i]) #获取该特征下的所有特征值
# print("{}---".format(fea_cls))
for j in fea_cls: #遍历所有特征值
newEqDataX,newEqDataY,newNeqDataX,newNeqDataY=splitDataSet(data_X,data_Y,i,j) #进行数据集切分 feaGini = #计算基尼指数
feaGini += newEqDataY.size/m*calcGini(newEqDataY) + newNeqDataY.size/m*calcGini(newNeqDataY)
if feaGini < minFeaGini:
bestFeature = i
bestFeaVal = j
minFeaGini = feaGini
return bestFeature,bestFeaVal #返回最优划分方式 def createTree(data_X,data_Y,fea_idx): #创建决策树
y_labels = np.unique(data_Y)
#.如果数据集中,所有实例都属于同一类,则返回
if y_labels.size == :
return data_Y[] #.如果特征集为空,表示遍历了所有特征,使用多数投票进行决定
if data_X.shape[] == :
bestFea,bestCnt = ,
for i in y_labels:
cnt = data_Y[np.where(data_Y==i)].size
if cnt > bestCnt:
bestFea = i
bestCnt = cnt
return bestFea #按照基尼指数,选择特征,进行继续递归创建树
bestFeature, bestFeaVal = chooseBestFeature(data_X,data_Y)
# print(bestFeature,bestFeaVal)
feaBestIdx = fea_idx[bestFeature]
my_tree = {feaBestIdx:{}}
#获取划分结果
newEqDataX,newEqDataY,newNeqDataX,newNeqDataY = splitDataSet(data_X,data_Y,bestFeature,bestFeaVal)
#删除我们选择的最优特征
newEqDataX = np.delete(newEqDataX,bestFeature,)
newNeqDataX = np.delete(newNeqDataX,bestFeature,) fea_idx = np.delete(fea_idx,bestFeature,) my_tree[feaBestIdx]["{}_{}".format(,bestFeaVal)] = createTree(newEqDataX,newEqDataY,fea_idx)
my_tree[feaBestIdx]["{}_{}".format(,bestFeaVal)] = createTree(newNeqDataX,newNeqDataY,fea_idx) return my_tree def preDealData(filename):
df = pd.read_table(filename,'\t',header = None)
columns = ["age","prescript","astigmatic","tearRate"] # df.columns = ["age","prescript","astigmatic","tearRate","Result"] #https://zhuanlan.zhihu.com/p/60248460 #数据预处理,变为可以处理的数据 #https://blog.csdn.net/liuweiyuxiang/article/details/78222818
new_df = pd.DataFrame()
for i in range(len(columns)):
new_df[i] = pd.factorize(df[i])[] ##factorize函数可以将Series中的标称型数据映射称为一组数字,相同的标称型映射为相同的数字。
data_X = new_df.values
data_Y = pd.factorize(df[df.shape[]-])[] #factorize返回的是ndarray类型
data_Y = np.array([data_Y]).T return data_X,data_Y,columns data_X,data_Y,fea_names = preDealData("lenses.txt")
print(data_X)
print(data_Y)
# data_x,data_y,fea_names = createDataSet()
fea_Idx = np.arange(len(fea_names)) # data_X,data_Y,fea_names = createDataSet()
# data_X = np.array(data_X)
# data_Y = np.array(data_Y)
#
# fea_Idx = np.arange(len(fea_names)) print(createTree(data_X,data_Y,fea_Idx))
除了计算基尼指数,其他大多同ID3算法一致。
(七)测试数据集


young myope no reduced no lenses
young myope no normal soft
young myope yes reduced no lenses
young myope yes normal hard
young hyper no reduced no lenses
young hyper no normal soft
young hyper yes reduced no lenses
young hyper yes normal hard
pre myope no reduced no lenses
pre myope no normal soft
pre myope yes reduced no lenses
pre myope yes normal hard
pre hyper no reduced no lenses
pre hyper no normal soft
pre hyper yes reduced no lenses
pre hyper yes normal no lenses
presbyopic myope no reduced no lenses
presbyopic myope no normal no lenses
presbyopic myope yes reduced no lenses
presbyopic myope yes normal hard
presbyopic hyper no reduced no lenses
presbyopic hyper no normal soft
presbyopic hyper yes reduced no lenses
presbyopic hyper yes normal no lenses
机器学习实战---决策树CART简介及分类树实现的更多相关文章
- 机器学习实战---决策树CART回归树实现
机器学习实战---决策树CART简介及分类树实现 一:对比分类树 CART回归树和CART分类树的建立算法大部分是类似的,所以这里我们只讨论CART回归树和CART分类树的建立算法不同的地方.首先,我 ...
- matlab实现cart(回归分类树)
作为机器学习的小白和matlab的小白自己参照 python的 <机器学习实战> 写了一下分类回归树,这里记录一下. 关于决策树的基础概念就不过多介绍了,至于是分类还是回归..我说不清楚. ...
- 机器学习实战 -- 决策树(ID3)
机器学习实战 -- 决策树(ID3) ID3是什么我也不知道,不急,知道他是干什么的就行 ID3是最经典最基础的一种决策树算法,他会将每一个特征都设为决策节点,有时候,一个数据集中,某些特征属 ...
- 机器学习实战笔记(Python实现)-02-决策树
--------------------------------------------------------------------------------------- 本系列文章为<机器 ...
- [机器学习&数据挖掘]机器学习实战决策树plotTree函数完全解析
在看机器学习实战时候,到第三章的对决策树画图的时候,有一段递归函数怎么都看不懂,因为以后想选这个方向为自己的职业导向,抱着精看的态度,对这本树进行地毯式扫描,所以就没跳过,一直卡了一天多,才差不多搞懂 ...
- [机器学习实战] 决策树ID3算法
1. 决策树特点: 1)优点:计算复杂度不高,输出结果易于理解,对中间值的缺失不敏感,可以处理不相关特征数据. 2)缺点:可能会产生过度匹配问题. 3)适用数据类型:数值型和标称型. 2. 一般流程: ...
- 用决策树(CART)解决iris分类问题
首先先看Iris数据集 Sepal.Length--花萼长度 Sepal.Width--花萼宽度 Petal.Length--花瓣长度 Petal.Width--花瓣宽度 通过上述4中属性可以预测花卉 ...
- 《机器学习实战》学习笔记第九章 —— 决策树之CART算法
相关博文: <机器学习实战>学习笔记第三章 —— 决策树 主要内容: 一.CART算法简介 二.分类树 三.回归树 四.构建回归树 五.回归树的剪枝 六.模型树 七.树回归与标准回归的比较 ...
- 03机器学习实战之决策树CART算法
CART生成 CART假设决策树是二叉树,内部结点特征的取值为“是”和“否”,左分支是取值为“是”的分支,右分支是取值为“否”的分支.这样的决策树等价于递归地二分每个特征,将输入空间即特征空间划分为有 ...
随机推荐
- docker-mcr 助您全速下载 dotnet 镜像
2018 年五月之后,微软将后续发布的所有 docker image 都推送到了 MCR (Miscrosoft Container Registry),但在中国大陆,它的速度实在是令人发指,本文将介 ...
- Redis 数据结构 之 SDS
SDS(simple dynamic string),简单动态字符串.s同时它被称为 Hacking String.hack 的地方就在 sds 保存了字符串的长度以及剩余空间.sds 的实现在 sd ...
- Springboot项目整合Swagger2报错
SpringBoot2.2.6整合swagger2.2.2版本的问题,启动SpringBoot报如下错: Error starting ApplicationContext. To display t ...
- user is not in the sudoers file
使用用户账户使用sudo来运行一些特权命令时出现了如下错误(sudo是一个允许特定的用户组用另一个用户(典型的是root)的特权来运行一个命令): user is not in the sudoers ...
- Java并发编程-深入Java同步器AQS原理与应用-线程锁必备知识点
并发编程中我们常会看到AQS这个词,很多朋友都不知道是什么东东,博主经过翻阅一些资料终于了解了,直接进入主题. 简单介绍 AQS是AbstractQueuedSynchronizer类的缩写,这个不用 ...
- 深入浅出PyTorch(算子篇)
Tensor 自从张量(Tensor)计算这个概念出现后,神经网络的算法就可以看作是一系列的张量计算.所谓的张量,它原本是个数学概念,表示各种向量或者数值之间的关系.PyTorch的张量(torch. ...
- web之robots.txt
什么是roots协议 robots协议也叫robots.txt(统一小写)是一种存放于网站根目录下的ASCII编码的文本文件,它通常告诉网络搜索引擎的漫游器(又称网络蜘蛛),此网站中的哪些内容是不应被 ...
- 读取和写入blob类型数据
读写oracle blob类型 http://zyw090111.iteye.com/blog/607869 http://blog.csdn.net/jeryjeryjery/article/de ...
- Linux下Jmeter+nmon+nmon analyser实现性能监控及结果分析
一.概述 前段时间讲述了Jmeter利用插件PerfMon Metrics Collector来监控压测过程中服务器资源的消耗,一个偶然机会,我发现nmon这个 工具挺不错,和Jmeter插件比起来, ...
- dll备份注意事项
test.dll20161111和test.dll同目录的时候,会报错!因为这样跟test1.dll(只是重名民)的效果是一样的,都会报错的. 同目录的情况下,应该改成test.dll.ddd. 为了 ...
