1. 定义

红黑树也是二叉查找树，我们知道，二叉查找树这一数据结构并不难，而红黑树之所以难是难在它是自平衡的二叉查找树，在进行插入和删除等可能会破坏树的平衡的操作时，需要重新自处理达到平衡状态。红黑树是一种含有红黑结点并能自平衡的二叉查找树，又称黑色完美平衡。

动画演示：https://rbtree.phpisfuture.com/

2. 节点称呼

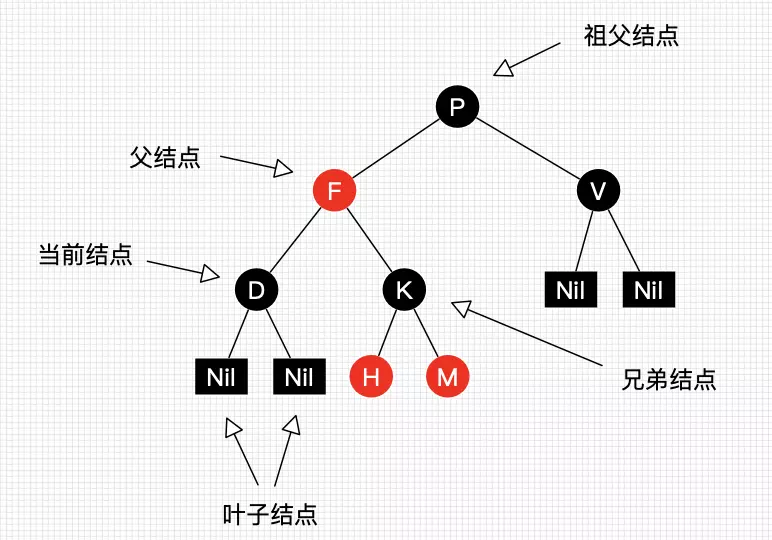
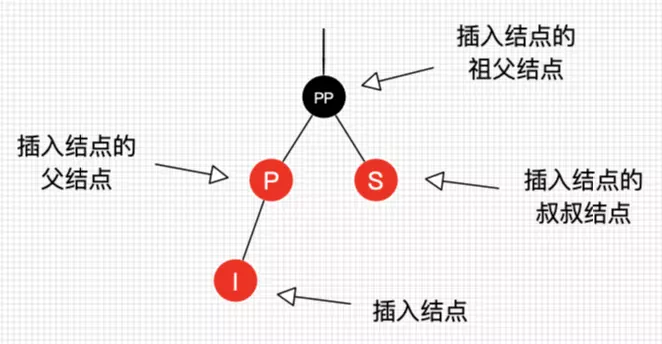
3. 性质

  • 每个节点要么是黑色，要么是红色。

  • 根节点一定是黑色。

  • 每个叶子节点（nil或null）都是黑色的。

  • 每个红节点的两个子节点一定是黑色的。（不可以同时存在两个相连的红结点，即：红节点的父结点与子结点都是黑的）

  • 从任意节点出发到每个叶子节点的路径都包含相同个数的黑色节点。

    1. * 如果一个结点存在黑子结点，那么该结点肯定有两个子结点。
    3. * 黑色完美平衡。

下面是一棵简单的红黑树，Nil（java中为null）是叶子节点并为黑色：

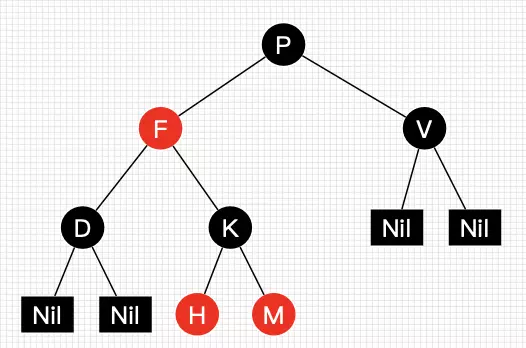
上图中的红黑树并不是完美平衡的二叉查找树，P节点的左边比右边高，但是左右黑色的层数是相等的，任意一个结点到叶子节点的黑色节点数都相同（性质5），也被成为黑色完美平衡。

4. 红黑树的自平衡

4.1 左旋

以某个结点作为支点(旋转结点)，其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子结点，其他结点保持不变。

4.2 右旋

以某个结点作为支点(旋转结点)，其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，其他结点保持不变。

4.3 变色

结点的颜色由红变黑或由黑变红。

5. 红黑树的查找

红黑树是一颗二叉平衡树，查找不会破坏平衡性，所以和二叉平衡术查找方式一致。

  • 从根节点开始查找，为空就返回null，为当前值就返回，否则继续向下查找。
  • 如果当前节点的key为要查找的节点的key，那么直接返回当前值。
  • 如果当前节点的key大于要查找的节点的key，那么继续向当前节点的左子节点查找。
  • 如果当前节点的key小于要查找的节点的key，那么继续向当前节点的右子节点查找。

6. 红黑树的插入

插入会破坏红黑树的黑色完美平衡，所以插入第一步要找到要插入的位置进行插入，第二步进行自平衡。

6.1 查找插入位置

所有插入操作都是在叶子结点进行的。

  • 插入节点的颜色肯定为红色。因为插入节点为黑色，就会破坏黑色完美平衡，使得到叶子节点的黑色数+1，而红色不会破坏。
  • 基本与红黑树的查找相同：

从根节点开始，如果根节点为空，则插入在根节点，否则根节点为当前节点。

  • 如果当前节点为null，则返回当前节点的父节点进行插入。
  • 如果当前节点的key等与插入节点的key，则更新当前节点的value。
  • 如果当前节点的key大于插入节点的key，则继续向当前节点的左子节点继续查找。
  • 如果当前节点的key小于插入节点的key，则继续向当前节点的右子节点继续查找。

6.2 插入的自平衡

插入主要指针指向插入结点，通过4. 红黑树的自平衡将红黑树达到的平衡即可

左旋

条件：当前节点的父节点是红色 & 当前节点的叔叔节点是黑色或者不存在 & 当前结点是其父节点的右子结点。

步骤：

  • 将父节点左旋
  • 将指针指向父结点

右旋

条件：当前节点的父节点是红色 & 当前节点的叔叔节点是黑色或者不存在 & 当前结点是其父节点的左子结点。

步骤：

  • 将父节点变为黑色
  • 将祖父结点变为红色
  • 将祖父结点右旋
  • 将指针指向祖父结点

变色

条件：当前节点的父节点是红色并且当前节点的叔叔节点也是红色。

步骤：

  • 当前结点是根结点直接变为黑色
  • 当前结点不是根结点
  • 将父节点与叔叔节点变为黑色
  • 将祖父结点变为红色
  • 将指针指向祖父结点

JDK1.8中插入自平衡的源码实现：

  1. private void fixAfterInsertion(Entry<K,V> x) {
  2.     x.color = RED;
  4.     while (x != null && x != root && x.parent.color == RED) {
  5.         // 插入的父节点是左子节点
  6.         if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
  7.             // y是插入节点的祖父节点的右子节点（叔叔节点）
  8.             Entry<K,V> y = rightOf(parentOf(parentOf(x)));
  9.             // y是红色
  10.             if (colorOf(y) == RED) {
  11.                 // 变色处理
  12.                 setColor(parentOf(x), BLACK);
  13.                 setColor(y, BLACK);
  14.                 setColor(parentOf(parentOf(x)), RED);
  15.                 // 指针指向插入节点的祖父节点
  16.                 x = parentOf(parentOf(x));
  17.             } else {
  18.             // y是黑色的
  19.                 // 插入节点是是父节点的右子节点
  20.                 if (x == rightOf(parentOf(x))) {
  21.                     // 父节点左旋
  22.                     x = parentOf(x);
  23.                     rotateLeft(x);
  24.                 }
  25.                 // 插入节点是是父节点的左节点
  26.                 setColor(parentOf(x), BLACK);
  27.                 setColor(parentOf(parentOf(x)), RED);
  28.                 // 祖父节点右旋
  29.                 rotateRight(parentOf(parentOf(x)));
  30.             }
  31.         } else {
  32.         // 插入的父节点是右子节点
  33.             // y是插入节点的祖父节点的左子节点（叔叔节点）
  34.             Entry<K,V> y = leftOf(parentOf(parentOf(x)));
  35.             // y是红色
  36.             if (colorOf(y) == RED) {
  37.                 // 变色处理
  38.                 setColor(parentOf(x), BLACK);
  39.                 setColor(y, BLACK);
  40.                 setColor(parentOf(parentOf(x)), RED);
  41.                 // 指针指向插入节点的祖父节点
  42.                 x = parentOf(parentOf(x));
  43.             } else {
  44.                 // 插入节点是是父节点的左子节点
  45.                 if (x == leftOf(parentOf(x))) {
  46.                     // 父亲节点右旋
  47.                     x = parentOf(x);
  48.                     rotateRight(x);
  49.                 }
  50.                 // 插入节点是是父节点的右子节点
  51.                 setColor(parentOf(x), BLACK);
  52.                 setColor(parentOf(parentOf(x)), RED);
  53.                 // 祖父节点左旋
  54.                 rotateLeft(parentOf(parentOf(x)));
  55.             }
  56.         }
  57.     }
  58.     root.color = BLACK;
  59. }

7. 红黑树删除

删除操作与插入差不多，查找、删除、自平衡。查找目标结点显然可以复用查找操作，当不存在目标结点时，忽略本次操作；当存在目标结点时，删除后就得做自平衡处理了。删除了结点后我们还需要找结点来替代删除结点的位置，不然子树跟父辈结点断开了，除非删除结点刚好没子结点，那么就不需要替代。

7.1 查找删除位置

基本与红黑树的查找相同：

  • 从根节点开始，如果根节点为空，则删除在根节点，否则根节点为当前节点。
  • 如果当前节点为null，则返回当前节点的父节点进行插入。
  • 如果当前节点的key等与删除节点的key，则找到当前节点。
  • 如果当前节点的key大于删除节点的key，则继续向当前节点的左子节点继续查找。
  • 如果当前节点的key小于删除节点的key，则继续向当前节点的右子节点继续查找。

7.2 删除结点

删除节点的可能情况：

JDK1.8中TreeMap删除可能性源代码实现：

  1. private void deleteEntry(Entry<K,V> p) {
  2.     modCount++;
  3.     size--;
  5.     // If strictly internal, copy successor's element to p and then make p
  6.     // point to successor.
  7.     // 如果删除节点有两个子节点
  8.     if (p.left != null && p.right != null) {
  9.         // 找到替代节点（很简单，自己看TreeMap源码）
  10.         Entry<K,V> s = successor(p);
  11.         p.key = s.key;
  12.         p.value = s.value;
  13.         p = s;
  14.     } // p has 2 children
  16.     // Start fixup at replacement node, if it exists.
  17.     // 如果有一个替换节点
  18.     Entry<K,V> replacement = (p.left != null ? p.left : p.right);
  20.     // 如果存在替换节点
  21.     if (replacement != null) {
  22.         // Link replacement to parent
  23.         replacement.parent = p.parent;
  24.         if (p.parent == null)
  25.             root = replacement;
  26.         else if (p == p.parent.left)
  27.             p.parent.left  = replacement;
  28.         else
  29.             p.parent.right = replacement;
  31.         // Null out links so they are OK to use by fixAfterDeletion.
  32.         p.left = p.right = p.parent = null;
  34.         // Fix replacement
  35.         if (p.color == BLACK)
  36.             fixAfterDeletion(replacement);
  37.     }
  38.     // 如果删除节点是根节点
  39.     else if (p.parent == null) { // return if we are the only node.
  40.         root = null;
  41.     } else {
  42.     // 没有子节点
  43.         if (p.color == BLACK)
  44.             fixAfterDeletion(p);
  46.         if (p.parent != null) {
  47.             if (p == p.parent.left)
  48.                 p.parent.left = null;
  49.             else if (p == p.parent.right)
  50.                 p.parent.right = null;
  51.             p.parent = null;
  52.         }
  53.     }
  54. }

7.3 删除后的自平衡

删除自平衡处理：

JDK1.8中TreeMap删除自平衡源代码实现：

  1. private void fixAfterDeletion(Entry<K,V> x) {
  2.     while (x != root && colorOf(x) == BLACK) {
  3.         // 删除节点是左子节点
  4.         if (x == leftOf(parentOf(x))) {
  5.             // sib是删除节点父节点的右子节点（兄弟节点）
  6.             Entry<K,V> sib = rightOf(parentOf(x));
  7.             // 兄弟节点是红色
  8.             if (colorOf(sib) == RED) {
  9.                 // 情况1.1处理
  10.                 setColor(sib, BLACK);
  11.                 setColor(parentOf(x), RED);
  12.                 rotateLeft(parentOf(x));
  13.                 sib = rightOf(parentOf(x));
  14.             }
  15.             // sib兄弟节点有两个黑色的子节点，情况2处理
  16.             if (colorOf(leftOf(sib))  == BLACK &&
  17.                 colorOf(rightOf(sib)) == BLACK) {
  18.                 // 变色
  19.                 setColor(sib, RED);
  20.                 // 指针指向删除节点的父节点
  21.                 x = parentOf(x);
  22.             } else {
  23.                 // 兄弟节点的右子节点是黑色
  24.                 if (colorOf(rightOf(sib)) == BLACK) {
  25.                     // 情况3.1.1处理
  26.                     setColor(leftOf(sib), BLACK);
  27.                     setColor(sib, RED);
  28.                     rotateRight(sib);
  29.                     sib = rightOf(parentOf(x));
  30.                 }
  31.                 // 情况3.1.2处理
  32.                 setColor(sib, colorOf(parentOf(x)));
  33.                 setColor(parentOf(x), BLACK);
  34.                 setColor(rightOf(sib), BLACK);
  35.                 rotateLeft(parentOf(x));
  36.                 // 跳出循环
  37.                 x = root;
  38.             }
  39.         } else { // symmetric
  40.         // 删除节点是右子节点
  41.             // sib是删除节点父节点的左子节点（兄弟节点）
  42.             Entry<K,V> sib = leftOf(parentOf(x));
  43.             // 兄弟节点是红色
  44.             if (colorOf(sib) == RED) {
  45.                 // 情况1.2处理
  46.                 setColor(sib, BLACK);
  47.                 setColor(parentOf(x), RED);
  48.                 rotateRight(parentOf(x));
  49.                 sib = leftOf(parentOf(x));
  50.             }
  51.             // sib兄弟节点有两个黑色的子节点，情况2处理
  52.             if (colorOf(rightOf(sib)) == BLACK &&
  53.                 colorOf(leftOf(sib)) == BLACK) {
  54.                 // 变色
  55.                 setColor(sib, RED);
  56.                 // 指针指向删除节点的父节点
  57.                 x = parentOf(x);
  58.             } else {
  59.                 // 兄弟节点的左子节点是黑色
  60.                 if (colorOf(leftOf(sib)) == BLACK) {
  61.                     // 情况3.2.1处理
  62.                     setColor(rightOf(sib), BLACK);
  63.                     setColor(sib, RED);
  64.                     rotateLeft(sib);
  65.                     sib = leftOf(parentOf(x));
  66.                 }
  67.                 // 情况3.2.2处理
  68.                 setColor(sib, colorOf(parentOf(x)));
  69.                 setColor(parentOf(x), BLACK);
  70.                 setColor(leftOf(sib), BLACK);
  71.                 rotateRight(parentOf(x));
  72.                 // 跳出循环
  73.                 x = root;
  74.             }
  75.         }
  76.     }
  78.     setColor(x, BLACK);
  79. }

参考

结语

欢迎关注微信公众号『码仔zonE』，专注于分享Java、云计算相关内容，包括SpringBoot、SpringCloud、微服务、Docker、Kubernetes、Python等领域相关技术干货，期待与您相遇！

彻底理解红黑树及JavaJDK1.8TreeMap源码分析的更多相关文章

  1. 《深入理解Spark：核心思想与源码分析》——SparkContext的初始化（叔篇）——TaskScheduler的启动

    <深入理解Spark:核心思想与源码分析>一书前言的内容请看链接<深入理解SPARK:核心思想与源码分析>一书正式出版上市 <深入理解Spark:核心思想与源码分析> ...

  2. 《深入理解Spark：核心思想与源码分析》（前言及第1章）

    自己牺牲了7个月的周末和下班空闲时间,通过研究Spark源码和原理,总结整理的<深入理解Spark:核心思想与源码分析>一书现在已经正式出版上市,目前亚马逊.京东.当当.天猫等网站均有销售 ...

  3. 《深入理解Spark：核心思想与源码分析》（第2章）

    <深入理解Spark:核心思想与源码分析>一书前言的内容请看链接<深入理解SPARK:核心思想与源码分析>一书正式出版上市 <深入理解Spark:核心思想与源码分析> ...

  4. 《深入理解Spark：核心思想与源码分析》一书正式出版上市

    自己牺牲了7个月的周末和下班空闲时间,通过研究Spark源码和原理,总结整理的<深入理解Spark:核心思想与源码分析>一书现在已经正式出版上市,目前亚马逊.京东.当当.天猫等网站均有销售 ...

  5. 《深入理解Spark：核心思想与源码分析》正式出版上市

    自己牺牲了7个月的周末和下班空闲时间,通过研究Spark源码和原理,总结整理的<深入理解Spark:核心思想与源码分析>一书现在已经正式出版上市,目前亚马逊.京东.当当.天猫等网站均有销售 ...

  6. 深入理解分布式调度框架TBSchedule及源码分析

    简介 由于最近工作比较忙,前前后后花了两个月的时间把TBSchedule的源码翻了个底朝天.关于TBSchedule的使用,网上也有很多参考资料,这里不做过多的阐述.本文着重介绍TBSchedule的 ...

  7. TreeMap源码分析，看了都说好

    概述 TreeMap也是Map接口的实现类,它最大的特点是迭代有序,默认是按照key值升序迭代(当然也可以设置成降序).在前面的文章中讲过LinkedHashMap也是迭代有序的,不过是按插入顺序或访 ...

  8. Java——HashMap底层源码分析

    1.简介 HashMap 根据键的 hashCode 值存储数据,大多数情况下可以直接定位到它的值,因而具有很快的访问速度,但遍历顺序却是不确定的. HashMap 最多只允许一条记录的key为 nu ...

  9. [JUC-5]ConcurrentHashMap源码分析JDK8

    在学习之前,最好先了解下如下知识: 1.ReentrantLock的实现和原理. 2.Synchronized的实现和原理. 3.硬件对并发支持的CAS操作及JVM中Unsafe对CAS的实现. 4. ...

随机推荐

  1. lua 优化

    彻底解析Android缓存机制——LruCache https://www.jianshu.com/p/b49a111147ee lua:部分常用操作的效率对比及代码优化建议(附测试代码) https ...

  2. HDU - 1272-小希的迷宫（连通图+环的判断）

    上次Gardon的迷宫城堡小希玩了很久(见Problem B),现在她也想设计一个迷宫让Gardon来走.但是她设计迷宫的思路不一样,首先她认为所有的通道都应该是双向连通的,就是说如果有一个通道连通了 ...

  3. 面试【JAVA基础】集合类

    1.ArrayList的扩容机制 每次扩容是原来容量的1.5倍,通过移位的方法实现. 使用copyOf的方式进行扩容. 扩容算法是首先获取到扩容前容器的大小.然后通过oldCapacity (oldC ...

  4. 9.深入k8s：调度器及其源码分析

    转载请声明出处哦~,本篇文章发布于luozhiyun的博客:https://www.luozhiyun.com 源码版本是1.19 这次讲解的是k8s的调度器部分的代码,相对来说比较复杂,慢慢的梳理清 ...

  5. require exports module.exports

    require 用于引入模块(js文件). JSON.或本地文件 自己写的模块必须是相对路径,省略了node就认为该自定义模块(js文件)是核心模块(内置模块或者第三方模块) node  有模块作用域 ...

  6. 在SQL中利用通项公式形成三角序列

    在前作 https://www.cnblogs.com/xiandedanteng/p/12735898.html中,我们可以用Java程序制成三角序列. 1, 2,2, 3,3,3, 4,4,4,4 ...

  7. RabbitMQ安装和运行

    RabbitMQ在Windows下安装和运行 1.下载Erlang: http://www.erlang.org/downloads/19.2 2.下载Windows版RabbitMq: http:/ ...

  8. python应用 曲线拟合 02

    前情提要 CsI 闪烁体晶体+PD+前放输出信号满足: $U(t) = \frac{N_f\tau_p}{\tau_p-\tau_f} \left[ e^{-\frac{t}{\tau_p}}-e^{ ...

  9. Django+pycharm+mysql 实现用户登录/注册（Django五）

    首先是让Django项目与mysql数据库初步建立连接 具体做法见:pycharm连接mysql(注意其中第二步MySQL驱动最好安装最新版的) 这里讲一下我在做这一步遇到的问题.一般Driver 那 ...

  10. virtualbox之紧虚拟主机与本地主机连接

    也就是手工配置IP地址.子网掩码.网关和DNS. 设置方法如下: vi /etc/sysconfig/network-scripts/ifcfg-eth0 编辑本地网卡的配置文件 主要查看下面这几项是 ...