20190531模拟赛总结&反思

T1:

来源：Codeforces -  Classroom Watch

Describe:

给出一个正整数 n，现在问存在多少个 x，使得  x在十进制下的每一位之和加上 x 等于 n。

Solution:

考场上一眼没看出来，之后又想了一会儿，想了一种比较常规的方法：

___

对于一个数 xyz （这里以三位数为例，另外位数同理），我们要让这个数与它各个数位上的和相加等于n，即：

100x+10y+z+x+y+z=101x+11y+2z=n

考后知道的确有dalao用了九重循环水过了，但我那个时候觉得效率太低，就觉得可以用深搜做，我开了这么一个数组：

num[11]={0,2,11,101,1001,10001,100001,1000001,10000001,100000001,1000000001}

对于当前递归到的每个数，从大到小减这些数，当该数组指针指向num[1]时，就进行判断当前枚举到的数能否被2整除，此外还有再判断剩下的数最大是否可能大于当前数，小于则之间返回。

然后，我就要写完这个方法时，时间已经过去了1个小时了...我突然想到，这个数既然是等于一个数加上各个数位上的数，那么这个数与原数之差绝对不会超过81，所以我们直接暴力就行。

我为了防止小的数可能出现一些特殊情况，我就在0-1000的范围内直接暴力，1000以上的数我再用上述做法。

悲剧的是...我再拆数的时候，对于每一个数本应该是temp = temp + x % 10，因为以前习惯性操作，我写成了temp = temp * 10 + x % 10...

虽然我再最后及时发现了，但是我只改了0-1000范围内的数，后面的因为我是粘贴了0-1000的做法，随意仍然是temp = temp * 10 + x % 10，然后就只拿到了20分。

以后对于粘贴上文内容还是得慎用！

Code:

#include<bits/stdc++.h>
using namespace std;

int n, ans[1000010], cnt = 0;

int main() {
  freopen("num.in", "r", stdin);
  freopen("num.out", "w", stdout);
    scanf("%d", &n);
    if (n <= 1000) {
    	for (int i = 1; i <= n; ++ i) {
    		int x = i;
    		int Temp = i;
    		while(x) {
    			Temp = Temp + x % 10;
    			x /= 10;
			}
			if (Temp == n) ans[++ cnt] = i;
		}
	}
	else {
		for (int i = n - 120; i <= n; ++ i) {
    		int x = i;
    		long long Temp = 0;
    		while(x) {
    			Temp = Temp * 10 + x % 10;
    			x /= 10;
			}
			if (Temp == n) ans[++ cnt] = i;
		}
	}
	printf("%d\n", cnt);
	for (int i = 1; i <= cnt; ++ i) printf("%d ", ans[i]); puts("");
	return 0;
}

T2:

应该是本校集训时候的出的题，就不放题面了。

给出三个数A,B,C，A-a=B-b=C-a-b=x，求出x.

Solution:

我们将这个等式拆开:

1.A-a=C-a-b,所以A=C-b;

2.B-b=C-a-b,所以B=C-a

3.A-a=B-b,所以A-B=a-b.

我们发现A+B-C=x，所以直接输出A-B+C即可。

Code:

#include<bits/stdc++.h>
using namespace std;

int T, A, B, C;

int main() {
  freopen("combo.in", "r", stdin);
  freopen("combo.out", "w", stdout);
	scanf("%d", &T);
	for (int i = 1; i <= T; ++ i) {
		scanf("%d%d%d", &A, &B, &C);
   		printf("%d\n", A + B - C);
	}
    return 0;
}

然后不知道什么原因，我在我考试的文件夹里只找到四个.in和.out，就是这题没有。所以...我freopen打错了...直接爆零...

我考完后改了过来就AC了...

虽然就算这道题按照满分来算了，我的分数也并不高，而且还有几个AK的大佬；对于之前的成绩来说，我最近的成绩的确处在下滑阶段，我却又只能看着这画面自叹不如？辛酸...

T3:

一个n*m的网格图，a[i][j]表示这个点上的高度，求表面积.

Solution:

我们只需计算左前或右后面的面积，乘两倍后同时加上两倍的n*m即可，我认为正常考试第二水的题。

Code:

#include<bits/stdc++.h>
using namespace std;

const int H = 110, W = 110;
int n, m, a[H][W];

int main() {
  freopen("surface.in", "r", stdin);
  freopen("surface.out", "w", stdout);
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; ++ i)
    	for (int j = 1; j <= m; ++ j)
    		scanf("%d", &a[i][j]);
    int Temp = 0;
    for (int i = 1; i <= n; ++ i)
    	for (int j = 1; j <= m; ++ j)
				Temp += max(a[i][j] - a[i][j - 1], 0) + max(a[i][j] - a[i - 1][j], 0);
	printf("%d\n", Temp * 2 + n * m * 2);
	return 0;
}

T4:

类比八皇后，在n*n的棋盘上，给出起始点和终止点，问起始点按1.向上两格向左一格;2.向上两格向右一格;3.向右两格;4.向下两格向右一格;5.向下两格向左一格;6.向左两格的方式进行移动，问到终止点的最少步数是多少。并说明路径，按以上顺序，分别是UL, UR, R, LR, LL, L。

Solution:

第一问广度优先搜索裸题，并在搜索时记录由谁转移而来，第二问通过该记录方式递归求出解，要注意递归时需将方向顺序倒置。

Code:

#include<bits/stdc++.h>
using namespace std;

const int N = 200;
int n, a, b, c, d;

int head, tail, q[40050][3], dis[N + 12][N + 21], pre[N + 10][N + 10][2];

void dfs(int x, int y) {
	if (x == a && y == b) return ;
	int x0 = pre[x][y][0], y0 = pre[x][y][1];
	dfs(x0, y0);
	if (x0 + 2 == x && y0 + 1 == y) printf("LR ");
	if (x0 + 2 == x && y0 - 1 == y) printf("LL ");
	if (x0 - 2 == x && y0 + 1 == y) printf("UR ");
	if (x0 - 2 == x && y0 - 1 == y) printf("UL ");
	if (x0 == x && y0 - 2 == y) printf("L ");
	if (x0 == x && y0 + 2 == y) printf("R ");
}

int main() {
  freopen("redqueen.in", "r", stdin);
  freopen("redqueen.out", "w", stdout);
    scanf("%d%d%d%d%d", &n, &a, &b, &c, &d);
    -- n;
    memset(dis, 0x3f, sizeof(dis));
    dis[a][b] = 0;
    q[tail = 1][0] = a, q[tail][1] = b;
    head = 0;
    while(head <= tail) {
    	int nx = q[++ head][0], ny = q[head][1];
    	if (dis[nx][ny] + 1 < dis[nx - 2][ny - 1] && nx - 2 >= 0 && ny - 1 >= 0) {
    		q[++ tail][0] = nx - 2;
    		q[tail][1] = ny - 1;
    		dis[nx - 2][ny - 1] = dis[nx][ny] + 1;
    		pre[nx - 2][ny - 1][0] = nx;
    		pre[nx - 2][ny - 1][1] = ny;
		}
    	if (dis[nx][ny] + 1 < dis[nx - 2][ny + 1] && nx - 2 >= 0 && ny + 1 <= n) {
    		q[++ tail][0] = nx - 2;
    		q[tail][1] = ny + 1;
    		dis[nx - 2][ny + 1] = dis[nx][ny] + 1;
    		pre[nx - 2][ny + 1][0] = nx;
    		pre[nx - 2][ny + 1][1] = ny;
		}
    	if (dis[nx][ny] + 1 < dis[nx][ny + 2] && ny + 2 <= n) {
    		q[++ tail][0] = nx;
    		q[tail][1] = ny + 2;
    		dis[nx][ny + 2] = dis[nx][ny] + 1;
    		pre[nx][ny + 2][0] = nx;
    		pre[nx][ny + 2][1] = ny;
		}
    	if (dis[nx][ny] + 1 < dis[nx + 2][ny + 1] && nx + 2 <= n && ny + 1 <= n) {
    		q[++ tail][0] = nx + 2;
    		q[tail][1] = ny + 1;
    		dis[nx + 2][ny + 1] = dis[nx][ny] + 1;
    		pre[nx + 2][ny + 1][0] = nx;
    		pre[nx + 2][ny + 1][1] = ny;
		}
    	if (dis[nx][ny] + 1 < dis[nx + 2][ny - 1] && nx + 2 <= n && ny - 1 >= 0) {
    		q[++ tail][0] = nx + 2;
    		q[tail][1] = ny - 1;
    		dis[nx + 2][ny - 1] = dis[nx][ny] + 1;
    		pre[nx + 2][ny - 1][0] = nx;
    		pre[nx + 2][ny - 1][1] = ny;
		}
    	if (dis[nx][ny] + 1 < dis[nx][ny - 2] && ny - 2 >= 0) {
    		q[++ tail][0] = nx;
    		q[tail][1] = ny - 2;
    		dis[nx][ny - 2] = dis[nx][ny] + 1;
    		pre[nx][ny - 2][0] = nx;
    		pre[nx][ny - 2][1] = ny;
		}
	}
	if (dis[c][d] == 0x3f3f3f3f) {
		puts("Impossible");
	}
	else {
		printf("%d\n", dis[c][d]);
		dfs(c, d);
		puts("");
	}
	return 0;
}

T5:

给出一个长度为n的序列a，并给出k,x，a[1]=1,a[n]=x，k为a[2...n-1]的取值范围，问序列中进行填数，使序列中相邻没有相同的数，求方案数%(1e9+7)的值。

Solution:

考场上推了一些，因为脑袋比较混，没有推出来，考后又推了一些，具体如下：

因为a[1]固定，所以a[2]有k-1种情况，a[2]固定，a[3]也有k-1种情况...a[n-2]有k-1种情况，而到了a[n-1]时，则需让a[n-1]既不等于a[n-2]，也不等于x.

显然我们需要考虑a[n-1]是某数的可能性，那么我们可以由a[n-2]的可能性推来（因为a[n-2]不像a[n-1]是特殊情况），在a[1...n-2]中，我们发现是有一定规律的，而2...k中的数所有的数不管目前i（i=1...n-2）是谁，每个数出现的可能性都是一样的，只有1有的次数有不同，所以我们可以把f[i]拆开（f[i]为1...k中所有数出现的方案数），一个为1的方案数，一个为2...k的方案数。

那我们将f[i]的值分开，即[i]为1的方案数和f[i]为2...k的方案数（2...k算一种），分别设为p,q。

i=1时,p=1,q=0;

i=2时,p=0,q=1;

i=3时,p=k-1,q=k-2.

我们发现t个1会产生t个2...k，t个2...k会产生t*(k-1)个1，t*(k-2)个2...k.

举个例子：

k=4时，

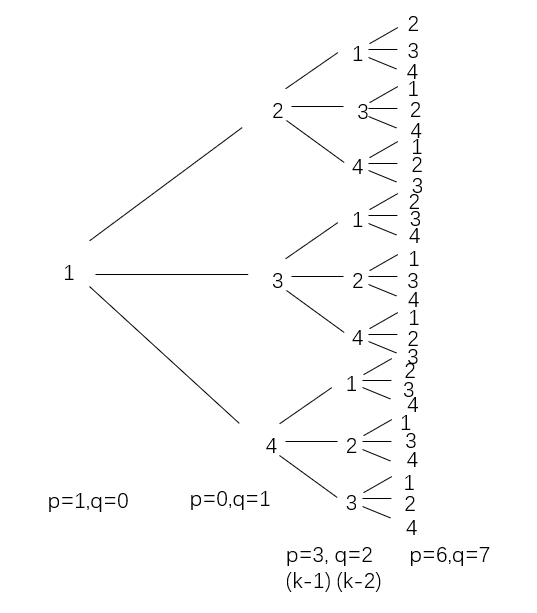
所以我们可以从3枚举至n-2，求出最后的p,q.

之后我们便可以对a[n-1]进行分类讨论了:

1. x=1:

当a[n-2]=1,a[n-1]可以取2...k中的任意数，则ans += p*(k-1) (2...k中有k-1个数);

当a[n-2]=2...k中的任意一数时，会产生k-2的贡献，因为2...k有k-1个数，则ans += q * (k - 2) * (k - 1);

2. x!==1:

当a[n-2]=1,a[n-1]可以取2...k中的任意不等于x的数，所以一个数产生的贡献为k-2，所以总贡献为q*(k-1)*(k-2);

当a[n-2]=2...k中的任意一数时，我们再进行讨论:

1.a[n-2]=x,会产生k-1的贡献，由于只有一个数，所以总贡献为q*(k-1).

2.a[n-2]!=x,每个数会产生k-2的贡献，这种情况有k-2个数，所以总贡献为q*(k-2)*(k-2).

但是这种做法不知道为什么在x=1的情况下通过了所有的数据点，但在x!=1时WA了好几个点，只有70分，至今不明白.

---

第二天：我们发现k是int类型的，那么(k-2)*(k-2)就爆int了，所以把k的类型改为long long就行...

Code:

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;

const int Mod = 1000000000 + 7;

int n, k, x;
ll ans = 0;

int main() {
  freopen("construct.in", "r", stdin);
  freopen("construct.out", "w", stdout);
    scanf("%d%d%d", &n, &k, &x);
	ll p = 0, q = 1;
	//p is the number of one, q is the number of the pair of 2...k
	for (int i = 3; i < n - 1; ++ i) {
		ll temp = p;
		p = q * (k - 1);
		p %= Mod;
		q *= (k - 2) % Mod;
		q += temp;
		q %= Mod;
	}
	if (x == 1) {
		ans += p * (k - 1);
		ans %= Mod;
		ans += q * (k - 2) % Mod * (k - 1);
		ans %= Mod;
	}
	else {
		ans += q * ((k - 2) % Mod * (k - 2) + k - 1);
		ans %= Mod;
		ans += p * (k - 2);
		ans %= Mod;
	}
	printf("%lld\n", ans % Mod);
	return 0;
}