dilated conv、deconv、fractional-strided conv

deconv的其中一个用途是做upsampling，即增大图像尺寸。

dilated convolution:

dilated conv，中文可以叫做空洞卷积或者扩张卷积。

首先是诞生背景，在图像分割领域，图像输入到CNN（典型的网络比如FCN[3]）中，FCN先像传统的CNN那样对图像做卷积再pooling，降低图像尺寸的同时增大感受野，但是由于图像分割预测是pixel-wise的输出，所以要将pooling后较小的图像尺寸upsampling到原始的图像尺寸进行预测（upsampling一般采用deconv反卷积操作）

之前的pooling操作使得每个pixel预测都能看到较大感受野信息。因此图像分割FCN中有两个关键，一个是pooling减小图像尺寸增大感受野，另一个是upsampling扩大图像尺寸。在先减小再增大尺寸的过程中，肯定有一些信息损失掉了，那么能不能设计一种新的操作，不通过pooling也能有较大的感受野看到更多的信息呢？答案就是dilated conv。

(a)图对应3x3的1-dilated conv，和普通的卷积操作一样，(b)图对应3x3的2-dilated conv，实际的卷积kernel size还是3x3，但是空洞为1，也就是对于一个7x7的图像patch，只有9个红色的点和3x3的kernel发生卷积操作，其余的点略过。也可以理解为kernel的size为7x7，但是只有图中的9个点的权重不为0，其余都为0。 可以看到虽然kernel size只有3x3，但是这个卷积的感受野已经增大到了7x7（如果考虑到这个2-dilated conv的前一层是一个1-dilated conv的话，那么每个红点就是1-dilated的卷积输出，所以感受野为3x3，所以1-dilated和2-dilated合起来就能达到7x7的conv）,(c)图是4-dilated conv操作，同理跟在两个1-dilated和2-dilated conv的后面，能达到15x15的感受野。对比传统的conv操作，3层3x3的卷积加起来，stride为1的话，只能达到(kernel-1)*layer+1=7的感受野，也就是和层数layer成线性关系，而dilated conv的感受野是指数级的增长。

 

dilated的好处是不做pooling损失信息的情况下，加大了感受野，让每个卷积输出都包含较大范围的信息。在图像需要全局信息或者语音文本需要较长的sequence信息依赖的问题中，都能很好的应用dilated conv，比如图像分割[3]、语音合成WaveNet[2]、机器翻译ByteNet[1]中。简单贴下ByteNet和WaveNet用到的dilated conv结构，可以更形象的了解dilated conv本身

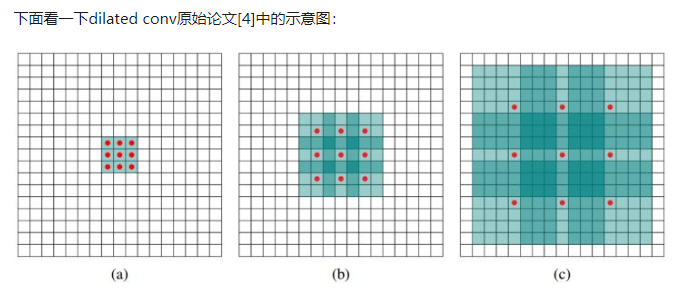
deconv的其中一个用途是做upsampling，即增大图像尺寸。而dilated conv并不是做upsampling，而是增大感受野。

可以形象的做个解释：

对于标准的k*k卷积操作，stride为s，分三种情况：

(1) s>1，即卷积的同时做了downsampling，卷积后图像尺寸减小；

(2) s=1，普通的步长为1的卷积，比如在tensorflow中设置padding=SAME的话，卷积的图像输入和输出有相同的尺寸大小；

(3) 0<s<1，fractionally strided convolution，相当于对图像做upsampling。比如s=0.5时，意味着在图像每个像素之间padding一个空白的像素后，stride改为1做卷积，得到的feature map尺寸增大一倍。

而dilated conv不是在像素之间padding空白的像素，而是在已有的像素上，skip掉一些像素，或者输入不变，对conv的kernel参数中插一些0的weight，达到一次卷积看到的空间范围变大的目的。

当然将普通的卷积stride步长设为大于1，也会达到增加感受野的效果，但是stride大于1就会导致downsampling，图像尺寸变小。大家可以从以上理解到deconv，dilated conv，pooling/downsampling，upsampling之间的联系与区别，欢迎留言沟通交流。

DCGAN[5]中使用deconv就更自然了，本身GAN就需要generative model，需要通过deconv从特定分布的输入数据中生成图片。GAN这种模式被Yann LeCun特别看好，认为是unsupervised learning的一个未来。

fractional-strided convolution：

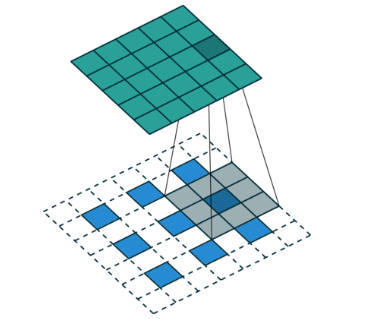
反卷积有时候也被叫做Fractionally Strided Convolution，翻译过来大概意思就是小数步长的卷积。对于步长 s>1的卷积，我们可能会想到其对应的反卷积步长 s′<1。

对于反卷积操作的小数步长我们可以理解为：在其输入特征单元之间插入 s−1 个0，插入0后把其看出是新的特征输入，然后此时步长 s′ 不再是小数而是为1。

详见网址：https://my.oschina.net/u/3702502/blog/1803358 http://www.mamicode.com/info-detail-2321005.html