零钱问题的动态规划解法——用 n 种不同币值的硬币凑出 m 元，最少需要多少硬币。

输入格式:
第一行输入需要凑的钱数 m 和硬币的种类 n （0<m<100，0<n<10），第二行输入 n 种硬币的具体币值，假设硬币供应量无限多。

输出格式:
输出最少需要的硬币个数

输入样例:
在这里给出一组输入。例如：

6 3
1 3 4
输出样例:
在这里给出相应的输出。例如：

2

代码实现：

package work5;

import java.util.Arrays;
import java.util.Scanner;

/**
* @author Noble4
*	maxValue[i][j]的意思是：拿的总金额为i，且正在拿面值为value[j]（当前最大值）的钱币的最少拿钱数目
*/
public class test6 {

public static void main(String[] args) {
int MAX_VALUE = 999;
Scanner sr = new Scanner(System.in);
//要凑的钱的总数
int c = sr.nextInt();
//钱的种类
int n = sr.nextInt();
//钱的价值
int[] value = new int[n];
for (int i = 0; i < n; i++) {
value[i] = sr.nextInt();
}
//对价值进行排序
Arrays.sort(value);
//构造最优解的网格
int[][] maxValue = new int[c+1][n];
for (int i = 0; i < c+1; i++) {
for (int j = 0; j < n; j++) {
maxValue[i][j] = MAX_VALUE;
}
}
// 填充网格
for (int i = 0; i <= c; i++) {
for (int j = 0; j < n; j++) {
if(i == 0) {
maxValue[i][j] = MAX_VALUE;
}else if(i<value[j]){//要凑钱数小于该种类钱面值时
if(j==0) {//如果这已经是最低面值的钱则表示此路不通
maxValue[i][j] = MAX_VALUE;
}else {//只能选择不拿
maxValue[i][j] = maxValue[i][j-1];
}
}else if(i%value[j] == 0) {//整除情况
maxValue[i][j] = i/value[j];
}else if(j == 0) {//如果这已经是最低面值且不能被整除则表示此路不通
maxValue[i][j] = MAX_VALUE;
}else {//可以选择拿该钱的情况
int item = (int) Math.floor(i/value[j]);
int result = MAX_VALUE;
for(int t = 0;t<=item;t++) {
int temp = maxValue[i-t*value[j]][j-1] + t;
if(temp<result) {
result = temp;
}
}
maxValue[i][j] = result;
}
}
}

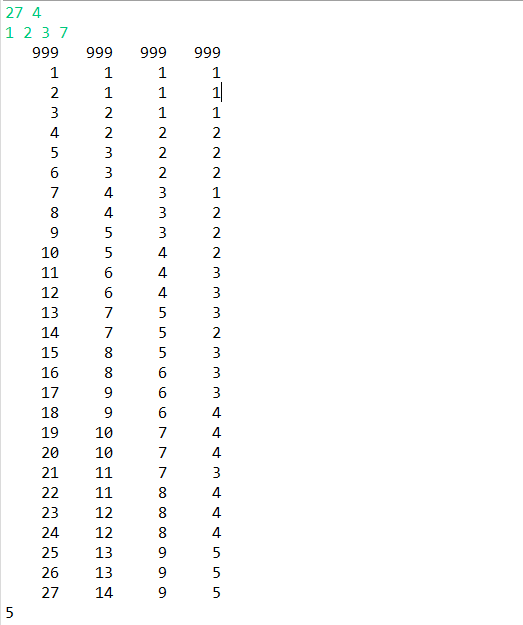
// 打印结果二维数组maxValue

for (int i = 0; i < c+1; i++) { for (int j = 0; j < n; j++) {
System.out.printf("%6d", maxValue[i][j]); } System.out.println(); }

System.out.println(maxValue[c][n-1]);
}
}

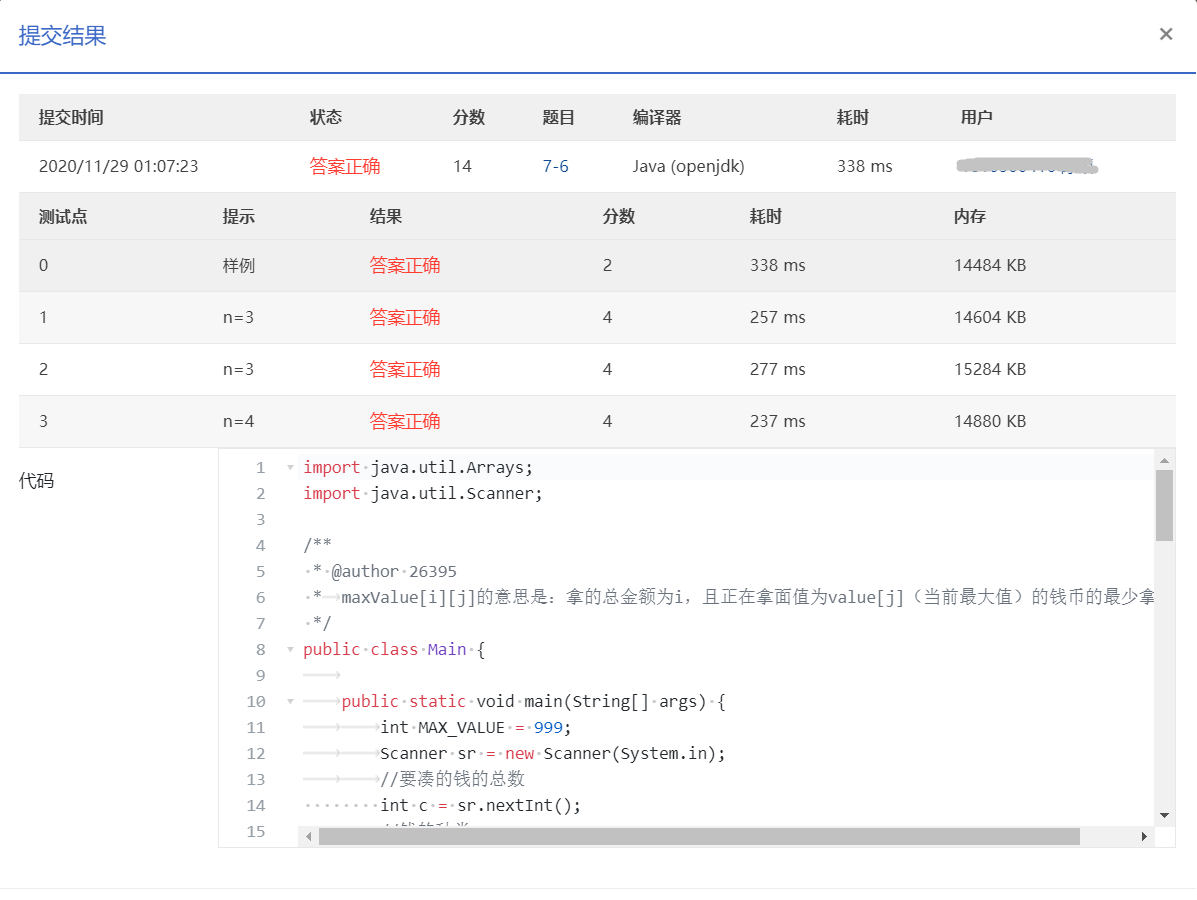
例程：

　　

BTA结果