前置技能：AC自动机

假设我们有了一个AC自动机，然后在上面进行字符串匹配。

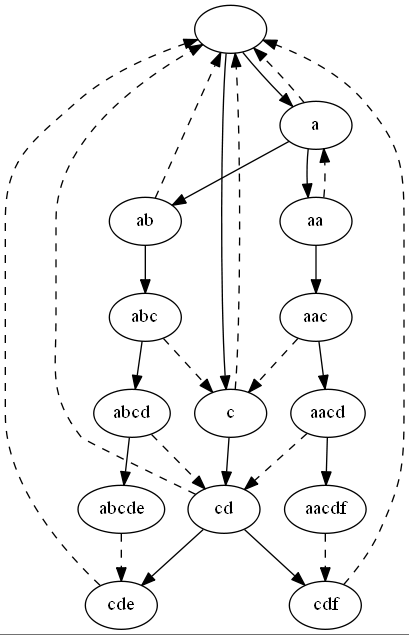
上面是一个有四个字符串的AC自动机（abcde、aacdf、cdf、cde），虚线是fail指针，实线是转移。

这是上一次讲AC自动机的时候的匹配代码：

int match(char* s)

{

    int cur=rot,ans=0;

    for(int i=0;s[i];i++)

    {

        int c=s[i]-'a'; cur=ch[cur][c];

        for(int f=cur;f!=rot;f=fail[f])

        ans+=cnt[f], cnt[f]=0;

    }

    return ans;

}

出题人嘿嘿一笑，给了你一个“aaaaaaaaaaaaaaaaaaa”。这样的字符串fail链长度为O(n)的，这就很尴尬了。

我们发现，如果我们把每个x与fail[x]连边，好像形成了一个树结构（fail[x]是x的父节点）。

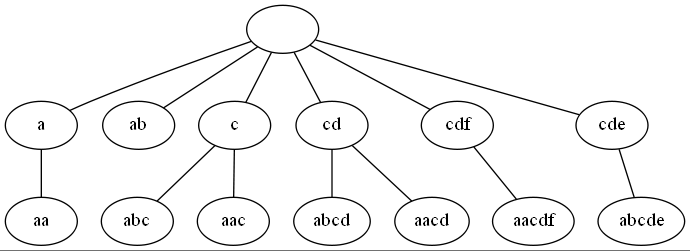
我们就是要查询一个点到根路径上的cnt之和！我们只要dfs一下预处理出来就行了。

我们来分析一下这个树结构是什么东西。

首先，这棵树是在一个trie的基础上产生的，所以这棵树上的每个点都是一个字符串的前缀，而且每个字符串的每个前缀在这棵树上都对应着一个点。

其次，由于fail指针，每个点父节点的字符串都是这个点字符串的后缀，并且树上没有更长的它的后缀。

例1 bzoj3172 单词

给出n个字符串，询问每个字符串在所有字符串中的出现次数之和。

在建ac自动机的时候，我们把经过的那条链的cnt值全部+1，那么我们就是要查询子树和。

为什么？例如有一个串abcde，匹配了123abcde123，那么AC自动机上123abcde就会在abcde的子树中。

#include <iostream>

#include <stdio.h>

#include <math.h>

#include <string.h>

#include <time.h>

#include <stdlib.h>

#include <string>

#include <bitset>

#include <vector>

#include <set>

#include <map>

#include <queue>

#include <algorithm>

#include <sstream>

#include <stack>

#include <iomanip>

using namespace std;

#define pb push_back

#define mp make_pair

typedef pair<int,int> pii;

typedef long long ll;

typedef double ld;

typedef vector<int> vi;

#define fi first

#define se second

#define fe first

#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}

#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}

#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}

#define es(x,e) (int e=fst[x];e;e=nxt[e])

#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])

#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}

#define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");}

using namespace std;

#define SZ 1000099

int rot=1,ch[SZ][27],fail[SZ],e=1;

ll cnt[SZ];

int M=0,fst[SZ],vb[SZ+SZ],nxt[SZ+SZ];

void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}

void adde(int a,int b){ad_de(a,b);ad_de(b,a);}

int insert(char* s)

{

    int cur=rot;

    for(int i=0;s[i];i++)

    {

        int c=s[i]-'a';

        if(!ch[cur][c]) ch[cur][c]=++e;

        cur=ch[cur][c]; ++cnt[cur];

    }

    return cur;

}

int qs[SZ],h=0,t=0;

void bfail()

{

    h=t=0; fail[rot]=rot;

    for(int i=0;i<26;i++)

    {

        if(!ch[rot][i])

        {

            ch[rot][i]=rot; continue;

        }

        fail[ch[rot][i]]=rot;

        qs[t++]=ch[rot][i];

    }

    while(h!=t)

    {

        int cur=qs[h++];

        for(int c=0;c<26;c++)

        {

            if(!ch[cur][c]) ch[cur][c]=ch[fail[cur]][c];

            else

            {

                fail[ch[cur][c]]=ch[fail[cur]][c];

                qs[t++]=ch[cur][c];

            }

        }

    }

}

int n,T,orz[SZ];

char str[SZ];

void dfs(int x,int f=0)

{

    for esb(x,e,b)

    {

        if(b==f) continue;

        dfs(b,x); cnt[x]+=cnt[b];

    }

}

int main()

{

    scanf("%d",&n);

    for(int i=1;i<=n;i++)

    {

        scanf("%s",str);

        orz[i]=insert(str);

    }

    bfail();

    for(int i=2;i<=e;i++)

        adde(i,fail[i]);

    dfs(1);

    for(int i=1;i<=n;i++)

        printf("%lld\n",cnt[orz[i]]);

}

例2 bzoj2434 阿狸的打字机

有一个打字机，上面有一个可以容纳字符串的凹槽。

打字机上有26个英文字母和'B'、'P'。输入字母，打字机的一个凹槽中会加入这个字母。按下'B'，打字机凹槽中会删掉最后一个字母。按下'P'，打字机会在纸上打印出凹槽中现有的所有字母并换行。按一下印有'B'的按键，打字机凹槽中最后一个字母会消失。

有m次询问，每次询问第x个打印的字符串在第y个打印的字符串中出现了多少次。

我们可以发现B就相当于回到trie上的父节点，P就相当于记录一下这个节点编号。

我们建出AC自动机和fail树。“第x个打印的字符串在第y个打印的字符串中出现了多少次”，如果树中只有第y个字符串那就是要统计x字符串这个点的子树和。

那么我们可以重新进行一次建树一样的操作，等到当前字符串为“第y个字符串”时再处理询问。我们只要在fail树上用dfs序+树状数组维护就行了。

#include <iostream>

#include <stdio.h>

#include <math.h>

#include <string.h>

#include <time.h>

#include <stdlib.h>

#include <string>

#include <bitset>

#include <vector>

#include <set>

#include <map>

#include <queue>

#include <algorithm>

#include <sstream>

#include <stack>

#include <iomanip>

using namespace std;

#define pb push_back

#define mp make_pair

typedef pair<int,int> pii;

typedef long long ll;

typedef double ld;

typedef vector<int> vi;

#define fi first

#define se second

#define fe first

#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}

#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}

#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}

#define es(x,e) (int e=fst[x];e;e=nxt[e])

#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])

#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}

#define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");}

using namespace std;

#define SZ 233333

int rot=1,ch[SZ][27],fail[SZ],fa[SZ],e=1;

int M=0,fst[SZ],vb[SZ+SZ],nxt[SZ+SZ];

void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}

void adde(int a,int b){ad_de(a,b);ad_de(b,a);}

char str[SZ];

int al(int& s) {if(!s) s=++e; return s;}

int n,rp[SZ];

void pre(char* s)

{

    int cur=rot;

    for(int i=0;s[i];i++)

    {

        if(s[i]=='B') cur=fa[cur];

        else if(s[i]=='P') rp[++n]=cur;

        else

        {

            char c=s[i]-'a';

            int nx=al(ch[cur][c]);

            fa[nx]=cur; cur=nx;

        }

    }

}

int qs[SZ],h=0,t=0;

void bfail()

{

    h=t=0; fail[rot]=rot;

    for(int i=0;i<26;i++)

    {

        if(!ch[rot][i])

        {

            ch[rot][i]=rot; continue;

        }

        fail[ch[rot][i]]=rot;

        qs[t++]=ch[rot][i];

    }

    while(h!=t)

    {

        int cur=qs[h++];

        for(int c=0;c<26;c++)

        {

            if(!ch[cur][c]) ch[cur][c]=ch[fail[cur]][c];

            else

            {

                fail[ch[cur][c]]=ch[fail[cur]][c];

                qs[t++]=ch[cur][c];

            }

        }

    }

    for(int i=2;i<=e;i++) adde(i,fail[i]);

}

int dfn[SZ],D=0,ls[SZ];

void dfs(int x,int f=0)

{

    dfn[x]=++D;

    for esb(x,e,b)

    {

        if(b==f) continue;

        dfs(b,x);

    }

    ls[x]=D;

}

int ss[SZ];

int sum(int x)

{

    int ans=0;

    for(;x>=1;x-=x&-x) ans+=ss[x];

    return ans;

}

void edt(int x,int y)

{

    for(;x<=D;x+=x&-x) ss[x]+=y;

}

int m,qa[SZ],qb[SZ],nq[SZ],fq[SZ],anss[SZ];

int main()

{

    scanf("%s",str); pre(str); bfail();

    scanf("%d",&m);

    for(int i=1;i<=m;i++)

    {

        scanf("%d%d",qa+i,qb+i);

        nq[i]=fq[qb[i]]; fq[qb[i]]=i;

    }

    dfs(rot);

    int cur=rot,ci=0;

    for(int i=0;str[i];i++)

    {

        if(str[i]=='B') edt(dfn[cur],-1), cur=fa[cur];

        else if(str[i]=='P')

        {

            ++ci;

            for(int q=fq[ci];q;q=nq[q])

                anss[q]=sum(ls[rp[qa[q]]])-sum(dfn[rp[qa[q]]]-1);

        }

        else

        {

            char c=str[i]-'a';

            int nx=ch[cur][c];

            fa[nx]=cur; cur=nx;

            edt(dfn[cur],1);

        }

    }

    for(int i=1;i<=m;i++) printf("%d\n",anss[i]);

}

例3 bzoj3881 Divljak

Alice有n个字符串s1...sn，Bob有一个字符串集合，一开始集合是空的。

若干个操作，每个操作是往集合里添加一个字符串或者给定x，查询集合中有多少个字符串包含sx。

注意这里要求的是有多少个包含，而不是出现了几次。

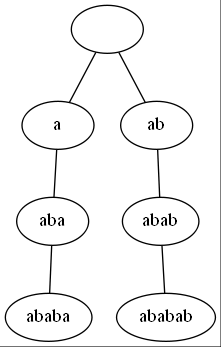
例如ababab和ab，如果算子树和的话就会被多算一次。

我们考虑上一题我们实际上干的事情是对于每个前缀对应的点，把根到这个点的路径全部+1。

那为了不重复统计，我们只要保证没有点被多次+1就行了。

上一题我们转化为了子树和，那么这一题转化为子树和只要在每个重复的lca处-1就行了，具体实现就类似虚树那样用一个栈来维护。

好像把虚树的板子抄下来就过了

#include <iostream>

#include <stdio.h>

#include <math.h>

#include <string.h>

#include <time.h>

#include <stdlib.h>

#include <string>

#include <bitset>

#include <vector>

#include <set>

#include <map>

#include <queue>

#include <algorithm>

#include <sstream>

#include <stack>

#include <iomanip>

using namespace std;

#define pb push_back

#define mp make_pair

typedef pair<int,int> pii;

typedef long long ll;

typedef double ld;

typedef vector<int> vi;

#define fi first

#define se second

#define fe first

#define FO(x) {freopen(#x".in","r",stdin);freopen(#x".out","w",stdout);}

#define Edg int M=0,fst[SZ],vb[SZ],nxt[SZ];void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}void adde(int a,int b){ad_de(a,b);ad_de(b,a);}

#define Edgc int M=0,fst[SZ],vb[SZ],nxt[SZ],vc[SZ];void ad_de(int a,int b,int c){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;vc[M]=c;}void adde(int a,int b,int c){ad_de(a,b,c);ad_de(b,a,c);}

#define es(x,e) (int e=fst[x];e;e=nxt[e])

#define esb(x,e,b) (int e=fst[x],b=vb[e];e;e=nxt[e],b=vb[e])

#define VIZ {printf("digraph G{\n"); for(int i=1;i<=n;i++) for es(i,e) printf("%d->%d;\n",i,vb[e]); puts("}");}

#define VIZ2 {printf("graph G{\n"); for(int i=1;i<=n;i++) for es(i,e) if(vb[e]>=i)printf("%d--%d;\n",i,vb[e]); puts("}");}

using namespace std;

#define SZ 2000099

int rot=1,ch[SZ][27],fail[SZ],e=1;

int M=0,fst[SZ],vb[SZ+SZ],nxt[SZ+SZ];

void ad_de(int a,int b){++M;nxt[M]=fst[a];fst[a]=M;vb[M]=b;}

void adde(int a,int b){ad_de(a,b);ad_de(b,a);}

int insert(char* s)

{

    int cur=rot;

    for(int i=0;s[i];i++)

    {

        int c=s[i]-'a';

        if(!ch[cur][c]) ch[cur][c]=++e;

        cur=ch[cur][c];

    }

    return cur;

}

int qs[SZ],h=0,t=0;

void bfail()

{

    h=t=0; fail[rot]=rot;

    for(int i=0;i<26;i++)

    {

        if(!ch[rot][i])

        {

            ch[rot][i]=rot; continue;

        }

        fail[ch[rot][i]]=rot;

        qs[t++]=ch[rot][i];

    }

    while(h!=t)

    {

        int cur=qs[h++];

        for(int c=0;c<26;c++)

        {

            if(!ch[cur][c]) ch[cur][c]=ch[fail[cur]][c];

            else

            {

                fail[ch[cur][c]]=ch[fail[cur]][c];

                qs[t++]=ch[cur][c];

            }

        }

    }

}

#define S 22

int n,T,up[SZ][S],dep[SZ],orz[SZ];

int dfn[SZ],ls[SZ],D=0;

char str[SZ];

void dfs(int x,int f=0)

{

    dfn[x]=++D; up[x][0]=f;

    for(int i=1;i<=S-1;i++)

        up[x][i]=up[up[x][i-1]][i-1];

    for esb(x,e,b)

    {

        if(b==f) continue;

        dep[b]=dep[x]+1;

        dfs(b,x);

    }

    ls[x]=D;

}

int jump(int x,int d)

{

    for(int i=S-1;i>=0;i--)

    {

        if(up[x][i]&&dep[up[x][i]]>=d)

            x=up[x][i];

    }

    return x;

}

int lca(int a,int b)

{

    if(dep[a]>dep[b])swap(a,b);

    //dep[a]<=dep[b]

    b=jump(b,dep[a]);

    if(a==b) return a;

    for(int i=S-1;i>=0;i--)

    {

        if(up[a][i]==up[b][i]) continue;

        a=up[a][i]; b=up[b][i];

    }

    return up[a][0];

}

int bs[SZ];

int sum(int x)

{

    int ans=0;

    for(;x>=1;x-=x&-x) ans+=bs[x];

    return ans;

}

int sum(int l,int r)

{return sum(r)-sum(l-1);}

void edt(int x,int y)

{

    for(;x<=D;x+=x&-x) bs[x]+=y;

}

int ss[SZ],sn=0,vfa[SZ];

bool cmpdfn(int a,int b)

{

    if(a!=b) return dfn[a]<dfn[b];

    return a<b;

}

int st[SZ],stn=0;

int vs[SZ],vn=0;

void inss(char* s)

{

    int l=strlen(s),cur=1;

    sn=stn=vn=0; ss[++sn]=1;

    for(int i=0;i<l;i++)

    {

        cur=ch[cur][s[i]-'a'];

        ss[++sn]=cur;

    }

    sort(ss+1,ss+1+sn,cmpdfn);

    sn=unique(ss+1,ss+1+sn)-ss-1;

    for(int i=1;i<=sn;i++) vs[++vn]=ss[i];

    for(int i=1;i<=sn;i++)

    {

        int x=ss[i];

        if(!stn) {st[++stn]=x; vfa[x]=0; continue;}

        int lc=lca(x,st[stn]);

        while(stn&&dep[st[stn]]>dep[lc])

        {

            if(dep[st[stn-1]]<=dep[lc])

                vfa[st[stn]]=lc;

            --stn;

        }

        if(st[stn]!=lc)

        {

            vs[++vn]=lc;

            vfa[lc]=st[stn];

            st[++stn]=lc;

        }

        vfa[x]=lc; st[++stn]=x;

    }

    for(int i=1;i<=vn;i++)

    {

        int v=vs[i];

        if(!vfa[v]) continue;

        edt(dfn[v],1);

        edt(dfn[vfa[v]],-1);

    }

}

int main()

{

    scanf("%d",&n);

    for(int i=1;i<=n;i++)

    {

        scanf("%s",str);

        orz[i]=insert(str);

    }

    bfail();

    for(int i=2;i<=e;i++) adde(i,fail[i]);

    dfs(1);

    int q; scanf("%d",&q);

    while(q--)

    {

        int g,x;

        scanf("%d",&g);

        if(g==1)

        scanf("%s",str), inss(str);

        else

        scanf("%d",&x),

        printf("%d\n",sum(dfn[orz[x]],ls[orz[x]]));

    }

}

fail树的更多相关文章

  1. BZOJ 2434: [Noi2011]阿狸的打字机 [AC自动机 Fail树 树状数组 DFS序]

    2434: [Noi2011]阿狸的打字机 Time Limit: 10 Sec  Memory Limit: 256 MBSubmit: 2545  Solved: 1419[Submit][Sta ...

  2. BZOJ 3172: [Tjoi2013]单词 [AC自动机 Fail树]

    3172: [Tjoi2013]单词 Time Limit: 10 Sec  Memory Limit: 512 MBSubmit: 3198  Solved: 1532[Submit][Status ...

  3. 【Codeforces163E】e-Government AC自动机fail树 + DFS序 + 树状数组

    E. e-Government time limit per test:1 second memory limit per test:256 megabytes input:standard inpu ...

  4. 【BZOJ-3881】Divljak AC自动机fail树 + 树链剖分+ 树状数组 + DFS序

    3881: [Coci2015]Divljak Time Limit: 20 Sec  Memory Limit: 768 MBSubmit: 508  Solved: 158[Submit][Sta ...

  5. 【BZOJ 2434】【NOI 2011】阿狸的打字机 fail树

    完全不会啊,看题解还看了好久,我是蒟蒻$QAQ$ $zyf$的题解挺好的:http://blog.csdn.net/clove_unique/article/details/51059425 $fai ...

  6. BZOJ2434 [Noi2011]阿狸的打字机（AC自动机 + fail树 + DFS序 + 线段树）

    题目这么说的: 阿狸喜欢收藏各种稀奇古怪的东西,最近他淘到一台老式的打字机.打字机上只有28个按键,分别印有26个小写英文字母和'B'.'P'两个字母.经阿狸研究发现,这个打字机是这样工作的: 输入小 ...

  7. 【BZOJ-2434】阿狸的打字机 AC自动机 + Fail树 + DFS序 + 树状数组

    2434: [Noi2011]阿狸的打字机 Time Limit: 10 Sec  Memory Limit: 256 MBSubmit: 2022  Solved: 1158[Submit][Sta ...

  8. NOI2011阿狸的打字机（fail树+DFS序）

    Description 阿狸喜欢收藏各种稀奇古怪的东西,最近他淘到一台老式的打字机.打字机上只有28个按键,分别印有26个小写英文字母和'B'.'P'两个字母. 经阿狸研究发现,这个打字机是这样工作的 ...

  9. AC自动机 & Fail树 专题练习

    Fail树就是AC自动机建出来的Fail指针构成的树. [bzoj3172][xsy1713]单词 题意 给定一些单词,求每个单词在所有单词里面的出现次数. 分析 构建Fail树,记录每个单词最后一个 ...

随机推荐

  1. Hawk 4.3 转换器

    转换器是最为常用的一种类型,当然它的使用也是最复杂的. 转换器有三种子类型: A:单文档->单文档:例如仅将某一列的字符提取出来 B:单文档->多文档:典型的如从爬虫转换,每一行url都可 ...

  2. [入门级] 基于 visual studio 2010 mvc4 的图书管理系统开发初步 （二）

    [入门级] 基于 visual studio 2010 mvc4 的图书管理系统开发初步 (二) Date  周六 10 一月 2015 By 钟谢伟 Category website develop ...

  3. 你真的会玩SQL吗？你所不知道的 数据聚合

    你真的会玩SQL吗?系列目录 你真的会玩SQL吗?之逻辑查询处理阶段 你真的会玩SQL吗?和平大使 内连接.外连接 你真的会玩SQL吗?三范式.数据完整性 你真的会玩SQL吗?查询指定节点及其所有父节 ...

  4. Linux系统修改PATH环境变量方法

    在Linux安装一些软件通常要添加路径环境变量PATH.PATH环境变量通俗的讲就是把程序的路径"备案"到系统中,这样执行这些程序时就不需要输入完整路径,直接在bash输入程序名就 ...

  5. 分享：使用 TypeScript 编写的 JavaScript 游戏代码

    <上篇博客>我写出了我一直期望的 JavaScript 大型程序的开发模式,以及 TS(TypeScript) 的一些优势.博客完成之后,我又花了一天时间试用 TS,用它来重构之前编写的一 ...

  6. Basic Tutorials of Redis(5) - Sorted Set

    The last post is mainly about the unsorted set,in this post I will show you the sorted set playing a ...

  7. 在Ubuntu|CentOS上安装Shutter截图工具及快捷键设置

    简介 Shutter前身叫GScrot,它是一款相当棒的截图软件. 通过Shutter,你可以截取包括选定区域.全屏幕.窗口.窗口内的控件甚至网页的图像.通过内置的强大插件机制,你可以在截图后,对图像 ...

  8. SQL Server 中怎么查看一个字母的ascii编码或者Unicode编码

    参考文章:微信公众号文章 在sql中怎么查看一个字符的ascii编码,so easy !! select ASCII('a') SELECT CHAR(97) charNum SELECT UNICO ...

  9. IdentityServer4 ASP.NET Core的OpenID Connect OAuth 2.0框架学习保护API

    IdentityServer4 ASP.NET Core的OpenID Connect OAuth 2.0框架学习之保护API. 使用IdentityServer4 来实现使用客户端凭据保护ASP.N ...

  10. Spring在web应用中获得Bean的方法

    一:使用ApplicationContext获得Bean 首先新建一个类,该类必须实现ApplicationContextAware接口,改接口有一个方法,public void setApplica ...