机器学习之Logistic 回归算法
声明:本篇博文是学习《机器学习实战》一书的方式路程,系原创,若转载请标明来源。
1 Logistic 回归算法的原理
1.1 需要的数学基础
我在看机器学习实战时对其中的代码非常费解,说好的利用偏导数求最值怎么代码中没有体现啊,就一个简单的式子:θ= θ - α Σ [( hθ(x(i))-y(i) ) ] * xi 。经过查找资料才知道,书中省去了大量的理论推导过程,其中用到了线性函数、sigmoid 函数、偏导数、最大似然函数、梯度下降法。下面让我们一窥究竟,是站在大神的肩膀描述我自己的见解。
1.2 Logistic 回归的引入
Logistic 回归是概率非线性模型,用于处理二元分类结果,名为回归实为分类。下面给出一个二元分类的例子,如下图所示:
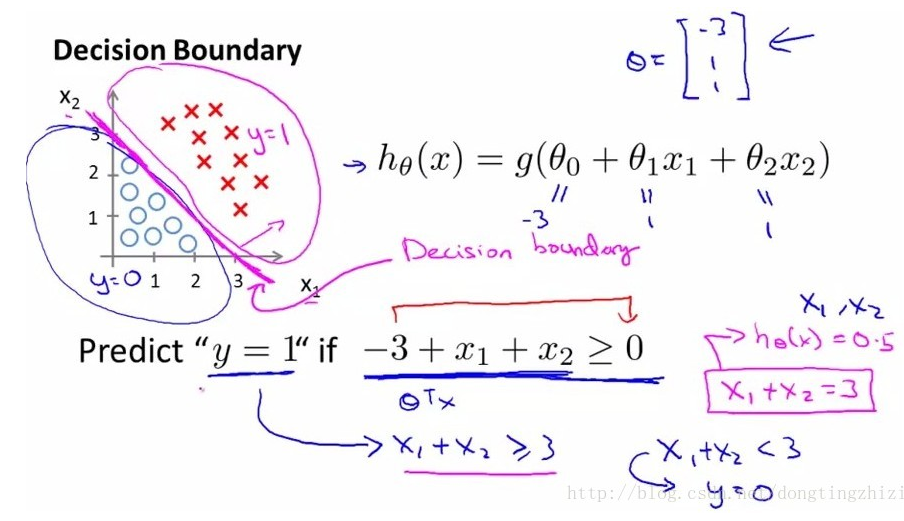
图中数据分成两类,打叉的一类用 y = 1 表示,另一类为圆圈用 y= 0 表示。现在我们要对数据进行分类,要找到一个分类函数(边界线),我们很容易得出一个线性函数对其分类:0 = θ0 + θ1x1 + θ2x2 。但我们想要的函数应该是,能接受所有的输入然后预测类别。例如:在两个分类的情况下,函数输出 0 或 1。因此,我们就需要引入Sigmoid 函数,这个函数的性质可以满足要求。Sigmoid 函数:
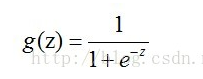
Sigmoid 函数的值域为(0,1),且具有良好的从0 到 1 的跳跃性,如在两个不同的坐标尺度下的函数图形:
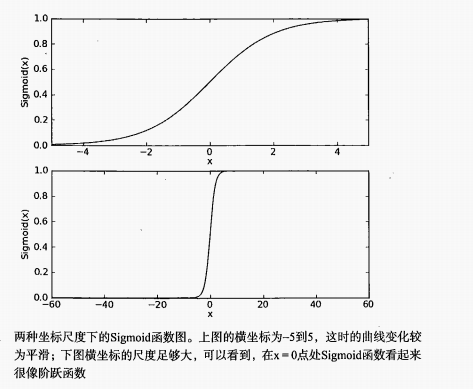
所以,我们把线性方程和Sigmoid 函数结合起来就能解决问题。即 :分类预测函数 hθ (x) = g( θ0 + θ1x1 + θ2x2) .我们就可以对样本数据进行分类,如下图所示:

对于线性的分类边界,如下形式:
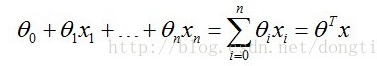
分类预测函数,如下形式:
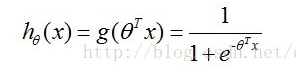
其中,θT 是向量 θ (θ0, θ1,... ,θn) 的转置,向量 x ( x0 , x1 ,... , xn),n -1为数据的维度,x0 =1,这是便于计算。
1.3 分类预测函数问题的转化成求θ
通过上面的分析,我们得出了分类预测函数 hθ(x) , 但其中向量 x 是已知的(x 是未知类别号的对象数据),向量 θ 未知,即我们把求分类函数问题转化成求向量 θ 。因为Sigmoid 函数的取值区间(0,1),那我们可以看做概率 P(y = 1 | xi ; θ)= hθ(x) , 表示在 xi 确定的情况下,类别 y = 1 的概率。由此,我们也可以得出在 xi 确定的情况下,类别 y = 0 的概率 P(y = 0 | xi ; θ)= 1 - P(y = 1 | xi ; θ)= 1 - hθ(x) . 即 :
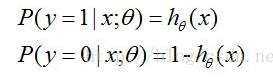
我们可以将这两个式子合并得:
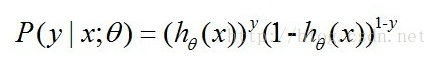
其中的 y = 0 或 1 .
这时候我们可以利用最大似然函数对向量 θ 求值,可以理解为选取的样本数据的概率是最大的,那么样本数为 m 的似然函数为:
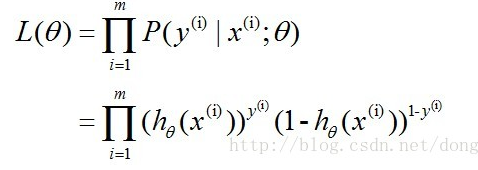
通过对数的形式对似然函数进行变化,对数似然函数:

这里的最大似然函数的值就是我们所要求的向量 θ , 而求解的方法利用梯度下降法。
1.4 梯度下降法求解θ
在用梯度下降法时,我们将会利用Sigmoid 函数的一个性质: g, (z) = g(z)[ 1- g(z) ] 。
构造一个Cost函数(损失函数),该函数表示预测的输出(h)与训练数据类别(y)之间的偏差,可以是二者之间的差(h-y)或者是其他的形式。综合考虑所有训练数据的“损失”,将Cost求和或者求平均,记为J(θ)函数,表示所有训练数据预测值与实际类别的偏差。
损失函数:
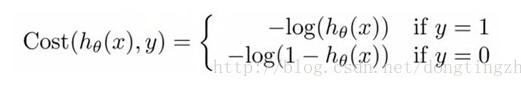
J(θ)代价函数:
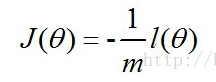

其中,x(i) 每个样本数据点在某一个特征上的值,即特征向量x的某个值,y(i) 是类别号,m 是样本对象个数。
梯度下降法含义:
梯度下降法,就是利用负梯度方向来决定每次迭代的新的搜索方向,使得每次迭代能使待优化的目标函数逐步减小。梯度其实就是函数的偏导数。
这里对用梯度下降法对 J (θ) 求最小值,与求似然函数的最大值是一样的。则 J(θ) 最小值的求解过程:
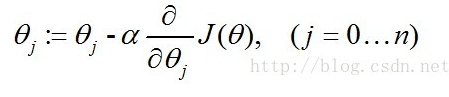
其中 α 是步长。
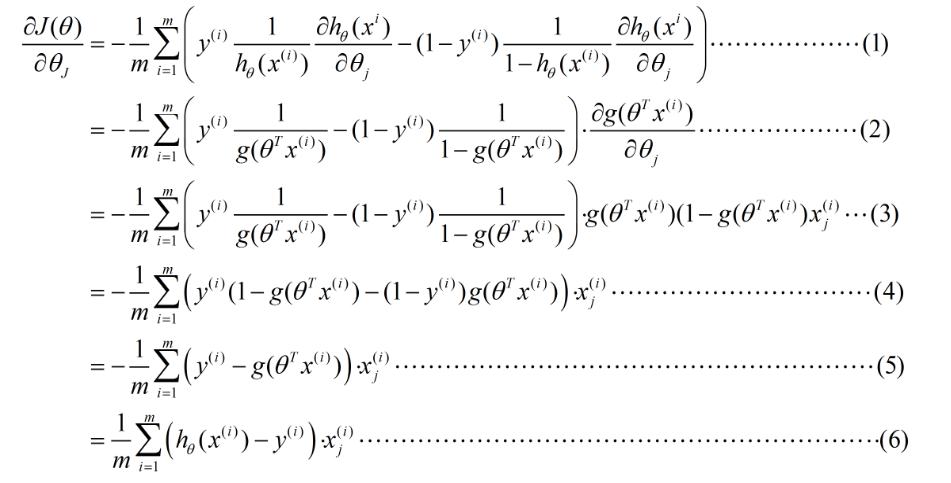
则可以得出:
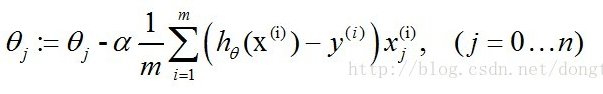
因为 α 是个常量,所以一般情况可以把 1/m 省去,省去不是没有用1/m ,只是看成 α 和1/m 合并成 α 。
最终式子为:
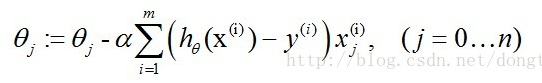
这就是一开始,我对代码中公式困惑的地方。在这里我在补充一点,以上的梯度下降法可以认为是批量梯度下降法(Batch Gradient Descent),由于我们有m个样本,这里求梯度的时候就用了所有m个样本的梯度数据。下面介绍随机梯度下降法(Stochastic Gradient Descent):
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的m个样本的数据,而是仅仅选取一个样本j来求梯度。随机梯度下降法,和4.1的批量梯度下降法是两个极端,一个采用所有数据来梯度下降,一个用一个样本来梯度下降。自然各自的优缺点都非常突出。对于训练速度来说,随机梯度下降法由于每次仅仅采用一个样本来迭代,训练速度很快,而批量梯度下降法在样本量很大的时候,训练速度不能让人满意。对于准确度来说,随机梯度下降法用于仅仅用一个样本决定梯度方向,导致解很有可能不是最优。对于收敛速度来说,由于随机梯度下降法一次迭代一个样本,导致迭代方向变化很大,不能很快的收敛到局部最优解。公式为:
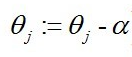
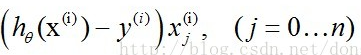
到这里已经把Logistics 回归的原理推导完成。这里对以上推导做一次总结:
边界线 ——> Sigmoid 函数 ——>求向量 θ ——> P(y=1 | x ; θ) = hθ(x) —— > 似然函数 l (θ) ——> 代价函数 J (θ) ——> 梯度下降法求解向量 θ ——> 最终公式 θj
2 使用python 实现Logistic 回归
2.1 Logistic 回归梯度上升优化算法
2.1.1 收集数据和处理数据
# 从文件中提取数据
def loadDataSet():
dataMat = [] ; labelMat = []
fr = open('testSet.txt')
for line in fr.readlines(): # 对文件的数据进行按行遍历
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr [0]), float(lineArr[1])])
labelMat.append(int(lineArr[2])) # 数据的类别号列表
return dataMat , labelMat
2.1.2 Sigmoid 函数
# 定义sigmoid 函数
def sigmoid(inX):
return longfloat( 1.0 / (1 + exp(-inX)))
使用longfloat() 是为防止溢出。
2.1.3 批量梯度上升算法的实现
# Logistic 回归梯度上升优化算法
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) # 将数列转化成矩阵
labelMat = mat(classLabels).transpose() # 将类标号转化成矩阵并转置成列向量
m,n = shape(dataMatrix) # 获得矩阵dataMatrix 的行、列数
alpha = 0.001 # 向目标移动的步长
maxCycles = 500 # 迭代次数
weights = ones((n ,1)) # 生成 n 行 1 列的 矩阵且值为1
for k in range(maxCycles):
h = sigmoid(dataMatrix*weights) # dataMatrix*weights 是 m * 1 的矩阵,其每一个元素都会调用sigmoid()函数,h 也是一个 m * 1 的矩阵
error = (labelMat - h) # 损失函数
weights = weights + alpha + dataMatrix.transpose()* error # 每步 weights 该变量
return weights.getA()
解释第 13 行代码:矩阵通过这个getA()这个方法可以将自身返回成一个n维数组对象 ,因为plotBestFit()函数中有计算散点x,y坐标的部分,其中计算y的时候用到了weights,如果weights是矩阵的话,weights[1]就是[0.48007329](注意这里有中括号!),就不是一个数了,最终你会发现y的计算结果的len()只有1,而x的len()则是60。
2.2 根据批量梯度上升法分析数据:画出决策边界
# 对数据分类的边界图形显示
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0] # 数据的行数,即对象的个数
xcord1 = []; ycord1 = [] # 对类别号为 1 的对象,分 X 轴和 Y 轴的数据
xcord2 = []; ycord2 = [] # 对类别号为 0 的对象,分 X 轴和 Y 轴的数据
for i in range(n): # 对所有的对象进行遍历
if int(labelMat[i])== 1: # 对象的类别为:1
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s') # 对散点的格式的设置,坐标号、点的大小、颜色、点的图形(方块)
ax.scatter(xcord2, ycord2, s=30, c='green') # 点的图形默认为圆
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]-weights[1]*x)/weights[2] # 线性方程 y = aX + b,y 是数据第三列的特征,X 是数据第二列的特征
ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2')
plt.show()
运行结果:
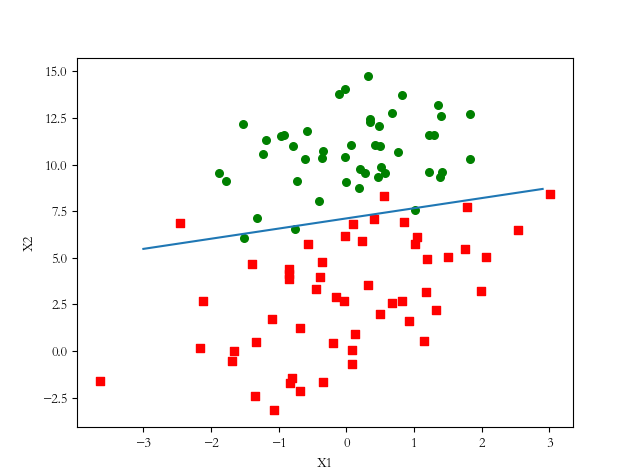
有结果效果图可知,边界线基本可以对样本进行较好的分类。
2.3 利用随机梯度上升法训练样本
# 随机梯度上升法
def stocGradAscent0(dataMatrix, classLabels, numIter=150):
m,n = shape(dataMatrix )
weights = ones(n)
for j in range(numIter): # 迭代次数
dataIndex = range(m) #
for i in range(m): # 对所有对象的遍历
alpha = 4/(1.0+j+i)+0.01 # 对步长的调整
randIndex = int (random.uniform(0,len(dataIndex))) # 随机生成一个整数,介于 0 到 m
h = sigmoid(sum(dataMatrix[randIndex]*weights)) # 对随机选择的对象计算类别的数值(回归系数值)
error = classLabels[randIndex] - h # 根据实际类型与计算类型值的误差,损失函数
weights = weights + alpha * error * dataMatrix[randIndex] # 每步 weights 改变值
del(dataIndex [randIndex]) # 去除已经选择过的对象,避免下次选中
return weights
在随机梯度上升法求解的 θ ,对样本进行分类,并画出其边界线,运行的结果图:
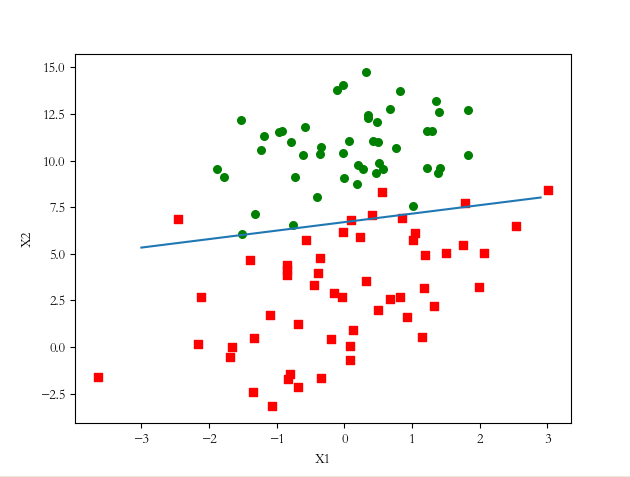
利用随机梯度上升法,通过150 次迭代得出的效果图和批量梯度上升法的效果图差不过,但随机梯度的效率比批量梯度上升法快很多。
3 实例:从疝气病症预测病马的死亡率
3.1 未知对象的预测
# 对未知对象进行预测类别号
def classifyVector(inX , weights):
prob = sigmoid(sum(inX * weights)) # 计算回归系数
if prob > 0.5:
return 1.0
else:
return 0.0
3.2 样本数据和测试函数
# 实例:从疝气病预测病马的死亡率
def colicTest():
frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt')# 数据文件
trainingSet = []; trainingLabels = [] # 样本集和类标号集的初始化
for line in frTrain.readlines():
currLine = line.strip().split('\t') # 根据制表符进行字符串的分割
lineArr =[]
for i in range(21):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[21]))
#trainWeights = stocGradAscent0(array(trainingSet), trainingLabels, 500) # 通过对训练样本计算出回归系数
trainWeights = gradAscent(array(trainingSet), trainingLabels) # 通过对训练样本计算出回归系数
errorCount = 0; numTestVec = 0.0 # 错误个数和错误率的初始化
# 预测样本的遍历
for line in frTest.readlines():
numTestVec += 1.0
currLine = line.strip().split('\t')
lineArr =[]
for i in range(21):
lineArr.append(float(currLine[i]))
if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]): # 预测的类别号与真实类别号的比较
errorCount += 1
errorRate = (float(errorCount)/numTestVec)
print u'本次测试的错误率是; %f' % errorRate
return errorRate
3.3 预测结果函数
# 预测结果函数
def multiTest():
numTests = 10; errorSum = 0.0
for k in range(numTests):
errorSum += colicTest()
print u'经过 %d 次测试结果的平均错误率是: %f ' % (numTests ,errorSum /float(numTests))
利用随机梯度上升法训练的样本集,测试结果:
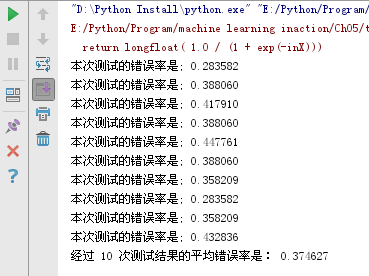
利用批量梯度上升法训练的样本集,测试结果:
附 完整程序
# coding:utf-8
from numpy import * # 从文件中提取数据
def loadDataSet():
dataMat = [] ; labelMat = []
fr = open('testSet.txt')
for line in fr.readlines(): # 对文件的数据进行按行遍历
lineArr = line.strip().split()
dataMat.append([1.0, float(lineArr [0]), float(lineArr[1])])
labelMat.append(int(lineArr[2])) # 数据的类别号列表
return dataMat , labelMat # 定义sigmoid 函数
def sigmoid(inX):
return longfloat( 1.0 / (1 + exp(-inX))) # Logistic 回归批量梯度上升优化算法
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) # 将数列转化成矩阵
labelMat = mat(classLabels).transpose() # 将类标号转化成矩阵并转置成列向量
m,n = shape(dataMatrix) # 获得矩阵dataMatrix 的行、列数
alpha = 0.001 # 向目标移动的步长
maxCycles = 500 # 迭代次数
weights = ones((n ,1)) # 生成 n 行 1 列的 矩阵且值为1
for k in range(maxCycles):
h = sigmoid(dataMatrix*weights) # dataMatrix*weights 是 m * 1 的矩阵,其每一个元素都会调用sigmoid()函数,h 也是一个 m * 1 的矩阵
error = (labelMat - h) # 损失函数
weights = weights + alpha + dataMatrix.transpose()* error # 每步 weights 该变量
return weights.getA() # 对数据分类的边界图形显示
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labelMat=loadDataSet()
dataArr = array(dataMat)
n = shape(dataArr)[0] # 数据的行数,即对象的个数
xcord1 = []; ycord1 = [] # 对类别号为 1 的对象,分 X 轴和 Y 轴的数据
xcord2 = []; ycord2 = [] # 对类别号为 0 的对象,分 X 轴和 Y 轴的数据
for i in range(n): # 对所有的对象进行遍历
if int(labelMat[i])== 1: # 对象的类别为:1
xcord1.append(dataArr[i,1]); ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1]); ycord2.append(dataArr[i,2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s') # 对散点的格式的设置,坐标号、点的大小、颜色、点的图形(方块)
ax.scatter(xcord2, ycord2, s=30, c='green') # 点的图形默认为圆
x = arange(-3.0, 3.0, 0.1)
y = (-weights[0]-weights[1]*x)/weights[2] # 线性方程 y = aX + b,y 是数据第三列的特征,X 是数据第二列的特征
ax.plot(x, y)
plt.xlabel('X1'); plt.ylabel('X2')
plt.show() # 随机梯度上升法
def stocGradAscent0(dataMatrix, classLabels, numIter=150):
m,n = shape(dataMatrix )
weights = ones(n)
for j in range(numIter): # 迭代次数
dataIndex = range(m) #
for i in range(m): # 对所有对象的遍历
alpha = 4/(1.0+j+i)+0.01 # 对步长的调整
randIndex = int (random.uniform(0,len(dataIndex))) # 随机生成一个整数,介于 0 到 m
h = sigmoid(sum(dataMatrix[randIndex]*weights)) # 对随机选择的对象计算类别的数值(回归系数值)
error = classLabels[randIndex] - h # 根据实际类型与计算类型值的误差,损失函数
weights = weights + alpha * error * dataMatrix[randIndex] # 每步 weights 改变值
del(dataIndex [randIndex]) # 去除已经选择过的对象,避免下次选中
return weights # 对未知对象进行预测类别号
def classifyVector(inX , weights):
prob = sigmoid(sum(inX * weights)) # 计算回归系数
if prob > 0.5:
return 1.0
else:
return 0.0 # 实例:从疝气病预测病马的死亡率
def colicTest():
frTrain = open('horseColicTraining.txt'); frTest = open('horseColicTest.txt')# 数据文件
trainingSet = []; trainingLabels = [] # 样本集和类标号集的初始化
for line in frTrain.readlines():
currLine = line.strip().split('\t') # 根据制表符进行字符串的分割
lineArr =[]
for i in range(21):
lineArr.append(float(currLine[i]))
trainingSet.append(lineArr)
trainingLabels.append(float(currLine[21]))
trainWeights = stocGradAscent0(array(trainingSet), trainingLabels, 500) # 通过随机梯度上升法计算回归系数
#trainWeights = gradAscent(array(trainingSet), trainingLabels) # 通过批量梯度上升法计算出回归系数
errorCount = 0; numTestVec = 0.0 # 错误个数和错误率的初始化
# 预测样本的遍历
for line in frTest.readlines():
numTestVec += 1.0
currLine = line.strip().split('\t')
lineArr =[]
for i in range(21):
lineArr.append(float(currLine[i]))
if int(classifyVector(array(lineArr), trainWeights))!= int(currLine[21]): # 预测的类别号与真实类别号的比较
errorCount += 1
errorRate = (float(errorCount)/numTestVec)
print u'本次测试的错误率是; %f' % errorRate
return errorRate # 预测结果函数
def multiTest():
numTests = 10; errorSum = 0.0
for k in range(numTests):
errorSum += colicTest()
print u'经过 %d 次测试结果的平均错误率是: %f ' % (numTests ,errorSum /float(numTests)) if __name__ == '__main__':
# 用批量梯度上升法画边界线
'''
dataSet, labelSet = loadDataSet()
#weights = gradAscent(dataSet, labelSet)
#plotBestFit(weights)
'''
# 用随机梯度上升法画边界线
'''
dataSet, labelSet = loadDataSet()
#weightss = stocGradAscent0(array(dataSet), labelSet )
#plotBestFit(weightss)
'''
# 实例的预测
multiTest()
机器学习之Logistic 回归算法的更多相关文章
- 机器学习之logistic回归算法与代码实现原理
Logistic回归算法原理与代码实现 本文系作者原创,转载请注明出处:https://www.cnblogs.com/further-further-further/p/10033567.html ...
- 机器学习算法-logistic回归算法
Logistic回归算法调试 一.算法原理 Logistic回归算法是一种优化算法,主要用用于只有两种标签的分类问题.其原理为对一些数据点用一条直线去拟合,对数据集进行划分.从广义上来讲这也是一种多元 ...
- [机器学习实战-Logistic回归]使用Logistic回归预测各种实例
目录 本实验代码已经传到gitee上,请点击查收! 一.实验目的 二.实验内容与设计思想 实验内容 设计思想 三.实验使用环境 四.实验步骤和调试过程 4.1 基于Logistic回归和Sigmoid ...
- Logistic回归算法梯度公式的推导
最近学习Logistic回归算法,在网上看了许多博文,笔者觉得这篇文章http://blog.kamidox.com/logistic-regression.html写得最好.但其中有个关键问题没有讲 ...
- 机器学习算法( 五、Logistic回归算法)
一.概述 这会是激动人心的一章,因为我们将首次接触到最优化算法.仔细想想就会发现,其实我们日常生活中遇到过很多最优化问题,比如如何在最短时间内从A点到达B点?如何投入最少工作量却获得最大的效益?如何设 ...
- logistic回归算法及其matlib实现
一般来说,回归不用在分类问题上,因为回归是连续型模型,而且受噪声影响比较大.如果非要使用回归算法,可以使用logistic回归. logistic回归本质上是线性回归,只是在特征到结果的映射中多加入了 ...
- 机器学习笔记—Logistic回归
本文申明:本系列笔记全部为原创内容,如有转载请申明原地址出处.谢谢 序言:what is logistic regression? Logistics 一词表示adj.逻辑的;[军]后勤学的n.[逻] ...
- matlib实现logistic回归算法(序一)
数据下载:http://archive.ics.uci.edu/ml/datasets/Adult 数据描述:http://archive.ics.uci.edu/ml/machine-learnin ...
- 机器学习笔记—Logistic 回归
前面我们介绍了线性回归,为捕获训练集中隐藏的线性模型,提高预测准确率,我们寻找最佳参数 θ,使得预测值与真实值误差尽量小,也就是使均方误差最小.而经过验证,最小均方误差是符合最大似然估计理论的. 在 ...
随机推荐
- [SDOI2009]晨跑
又是一道山东省选的题目,居然题目又十分水100行的代码就随随便便AC了. Description Elaxia最近迷恋上了空手道,他为自己设定了一套健身计划,比如俯卧撑.仰卧起坐等 等,不过到目前为止 ...
- MySQL Windows版安装详解
一.下载MySQL MySQL官网https://dev.mysql.com提供了Windows下的安装版msi和解压版zip,其中均包含32和64位版本,mis版本与SqlServer安装基本一致N ...
- 入门VMware Workstation下的Debian学习之基本命令(二)
本章记录如何在Linux终端进行命令操作命令下载路径,模拟终端.dkpg管理软件包.用户组和用户管理.文件属性.文件与目录管理.查看磁盘使用量. (1)命令下载路径: wegt 路径; (2)模拟终端 ...
- try catch finally 中包含return的几种情况,及返回结果
当当当,兴致勃勃的第二篇博客,散花~ 下面是正题(敲黑板) 第一种情况:在try和catch中有return,finally中没有return,且finally中没有对try或catch中要 retu ...
- Java面向对象 线程技术--上篇
Java面向对象 线程 知识概要: (1)线程与进程 (2)自定义线程的语法结构 (3)多线程概念理解 (4)多线程状态图 (5)多线程--卖票 (6)同 ...
- PPLB条码打印
using System; using System.Collections.Generic; using System.ComponentModel; using System.Data; usin ...
- 使用Fabric一键批量部署上线/线上环境监控
本文讲述如何使用fabric进行批量部署上线的功能 这个功能对于小应用,可以避免开发部署上线的平台,或者使用linux expect开发不优雅的代码. 前提条件: 1.运行fabric脚本的机器和其他 ...
- 在Visual Studio 2013 中使用C++单元测试
本文主要介绍在Visual Studio 2013中对代码进行单元测试的方法,包含了两方面的内容:对已有的Dll文件进行单元测试,以及对已有的源文件进行单元测试. 1. VS2013对DLL文件的单元 ...
- 数据挖掘 ID3
本文讲的是数据挖掘中的ID3,这个有很多人做了,我也没有说什么改善,只是要考试,用我考试记录的来写,具有很大主观性,如果看到有觉得不对或感觉不好,请关掉浏览器或和我说,请不要生气或发不良的言论. 决策 ...
- Web安全学习笔记(一)
Web安全学习笔记(一): URL协议 HTTP协议 1. URL 2. HTTP协议 什么是HTTP HTTP的工作原理 HTTP报文 什么是Cookies HTTP请求方式 Referer请求的功 ...
