OpenCV探索之路（四）：膨胀、腐蚀、开闭运算

腐蚀和膨胀是最基本的形态学运算。

腐蚀和膨胀是针对白色部分（高亮部分）而言的。

膨胀就是对图像高亮部分进行“领域扩张”，效果图拥有比原图更大的高亮区域；腐蚀是原图中的高亮区域被蚕食，效果图拥有比原图更小的高亮区域。

膨胀

膨胀就是求局部最大值的操作，从图像直观看来，就是将图像光亮部分放大，黑暗部分缩小。

#include<opencv2\opencv.hpp>
#include<opencv2\highgui\highgui.hpp>

using namespace std;
using namespace cv;

//膨胀
int main()
{
	Mat img = imread("lol1.jpg");
	namedWindow("原始图", WINDOW_NORMAL);
	imshow("原始图", img);
	Mat out;
	//获取自定义核
	Mat element = getStructuringElement(MORPH_RECT, Size(15, 15)); //第一个参数MORPH_RECT表示矩形的卷积核，当然还可以选择椭圆形的、交叉型的
	//膨胀操作
	dilate(img, out, element);
	namedWindow("膨胀操作", WINDOW_NORMAL);
	imshow("膨胀操作", out);
	waitKey(0);

}

可以看到，图像原来光亮的部分被放大了，黑暗的部分被缩小了。

腐蚀

#include<opencv2\opencv.hpp>
#include<opencv2\highgui\highgui.hpp>

using namespace std;
using namespace cv;

//腐蚀
int main()
{
	Mat img = imread("lol1.jpg");
	namedWindow("原始图", WINDOW_NORMAL);
	imshow("原始图", img);
	Mat out;
	//获取自定义核
	Mat element = getStructuringElement(MORPH_RECT, Size(15, 15)); //第一个参数MORPH_RECT表示矩形的卷积核，当然还可以选择椭圆形的、交叉型的
	//腐蚀操作
	erode(img, out, element);
	namedWindow("腐蚀操作", WINDOW_NORMAL);
	imshow("腐蚀操作", out);
	waitKey(0);

}

可以看到，图像原来黑暗的部分被放大了，明亮的部分被缩小了。

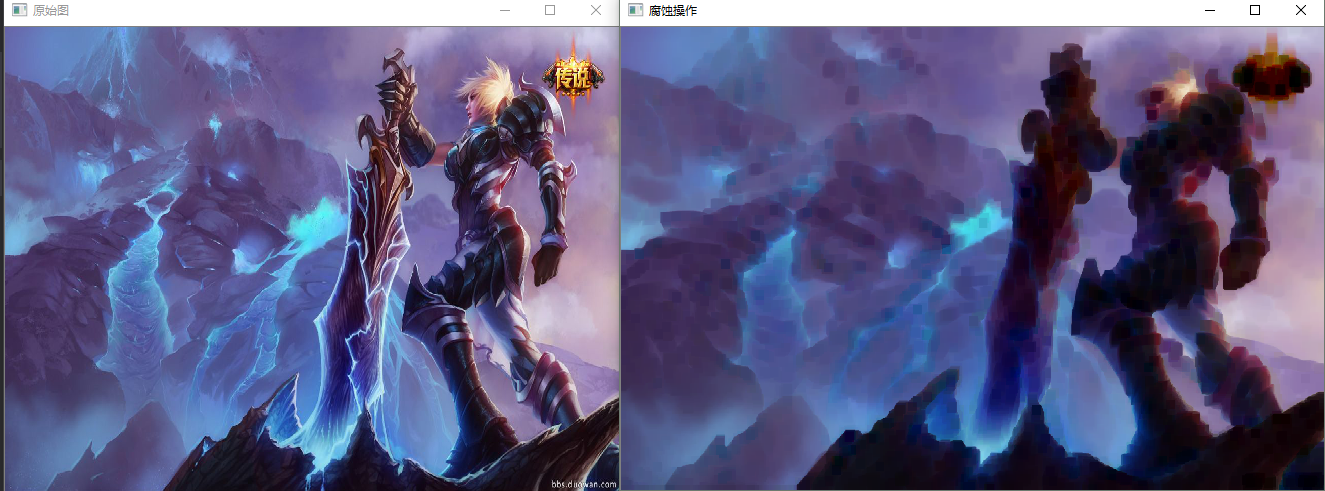
开运算：先腐蚀再膨胀，用来消除小物体

闭运算：先膨胀再腐蚀，用于排除小型黑洞

形态学梯度：就是膨胀图与俯视图之差，用于保留物体的边缘轮廓。

顶帽：原图像与开运算图之差，用于分离比邻近点亮一些的斑块。

黑帽：闭运算与原图像之差，用于分离比邻近点暗一些的斑块。

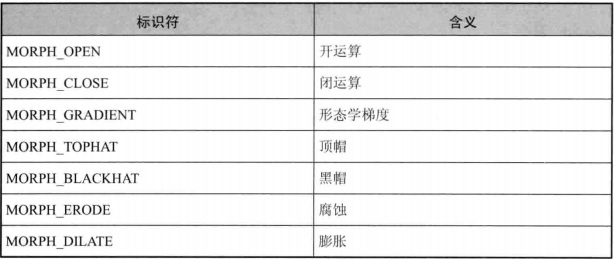
opencv里有一个很好的函数getStructuringElement，我们只要往这个函数传相应的处理参数，就可以进行相应的操作了，使用起来非常方便。

下面列举一下相应的操作宏定义。

#include<opencv2\opencv.hpp>
#include<opencv2\highgui\highgui.hpp>

using namespace std;
using namespace cv;

//高级形态学处理
int main()
{
	Mat img = imread("lol1.jpg");
	namedWindow("原始图", WINDOW_NORMAL);
	imshow("原始图", img);
	Mat out;
	//获取自定义核
	Mat element = getStructuringElement(MORPH_RECT, Size(15, 15)); //第一个参数MORPH_RECT表示矩形的卷积核，当然还可以选择椭圆形的、交叉型的

	//高级形态学处理，调用这个函数就可以了，具体要选择哪种操作，就修改第三个参数就可以了。这里演示的是形态学梯度处理
	morphologyEx(img, out, MORPH_GRADIENT, element);
	namedWindow("形态学处理操作", WINDOW_NORMAL);
	imshow("形态学处理操作", out);
	waitKey(0);

}

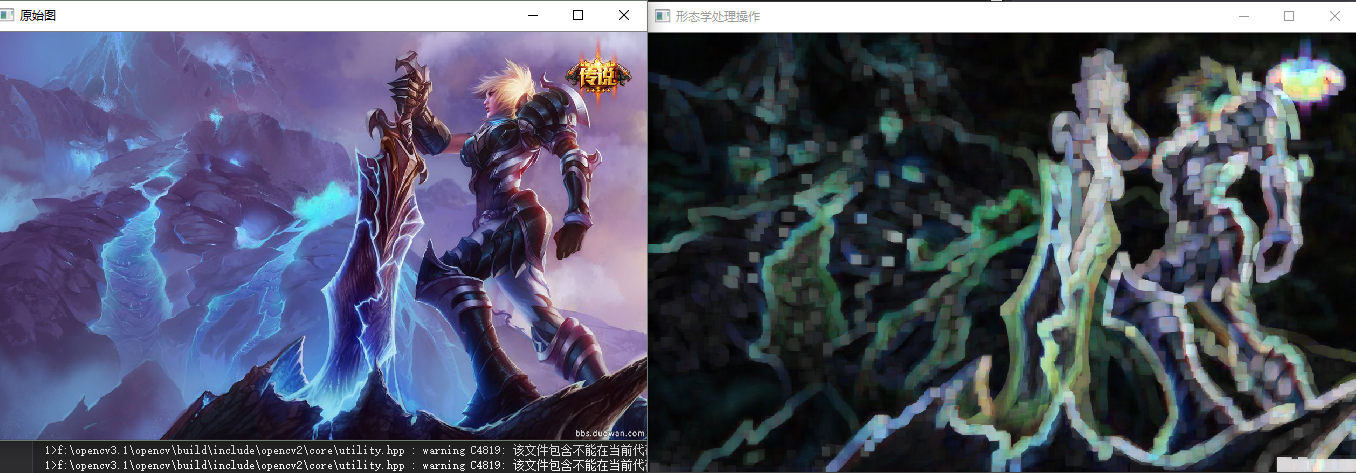
形态学梯度处理

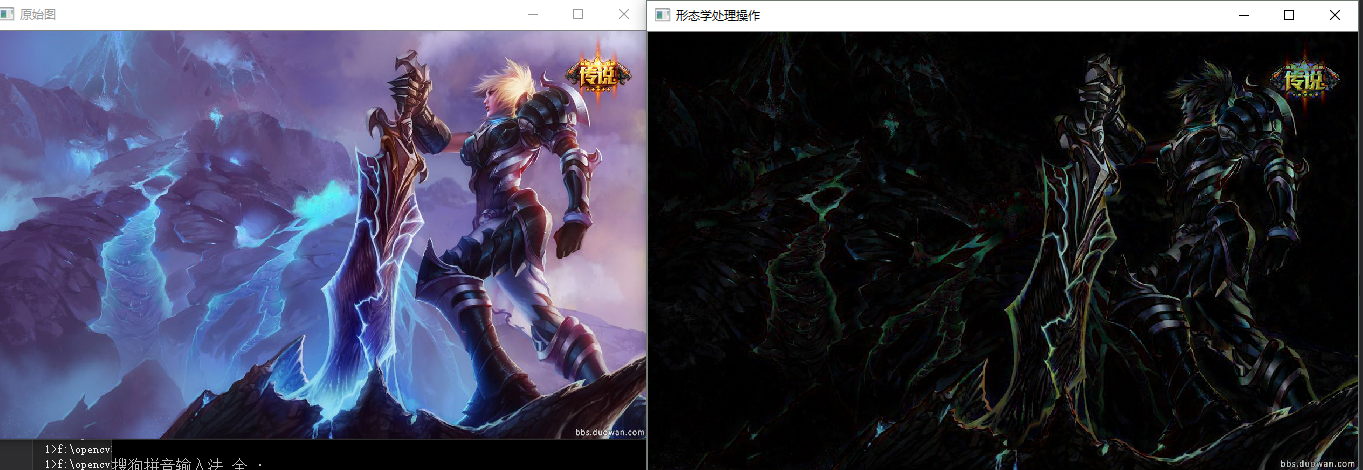
这个是顶帽运算的效果