【js数据结构】可逐次添加叶子的二叉树(非最优二叉树)
最近小菜鸟西瓜莹看到了一道面试题:
给定二叉树,按层打印。例如1的子节点是2、3, 2的子节点是3、4, 5的子节点是6,7.
需要建立如图二叉树:
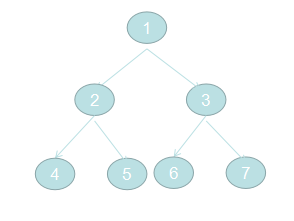
但是西瓜莹找到的相关代码都是用js构建最优二叉树,假如,依次向二叉树中添加4,2,6,1,3,5,7最优二叉树如图:

比根节点小的节点总是放在根节点的左节点上,比根节点大的节点总是放在根节点的右节点上。
假如想依次向二叉树添加1,2,3,4,5,6,7 二叉树又是如何呢?
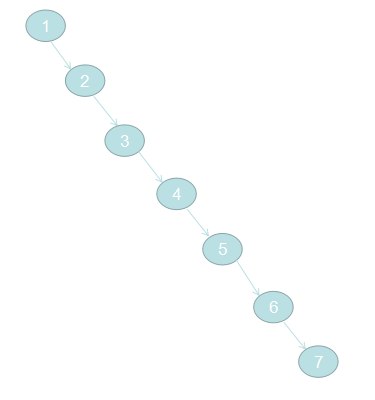
后一个数据总是比前一个数据大,那么就会一直在根节点的右节点上。
构建最优二叉树的核心就是添加节点的函数,记录当前节点,如果新数据比当前节点小,则让新数据成为左节点。否则成为右节点。
代码如下:
function addNode(ele){
var n = new Node(ele, null, null);
var Que = [];
if(this.root == null)
{
this.root = n;
}
else {
var curr = this.root;
var parent;
while(true)
{
parent = curr;
if(ele<curr.element)
{
curr = curr.left;
if( curr == null)
{
parent.left = n;
break;
}
}
else{
curr = curr.right;
if(curr == null)
{
parent.right = n;
break;
}
}
}
}
}
}
可是目的并不是创建最优二叉树,而是创建1,2,3,4,5,6,7这样的二叉树,那么如何实现呢?
思路:用一个队列来存储节点,将根节点放入队列中,如果根节点既有左节点又有右节点,将左右节点放入队列,如果没有左节点,将新数据放在左节点上,如果没有右节点,就将新数据放在右节点上。
代码:
function addNode(ele){
var n = new Node(ele, null, null);
var Que = [];
if(this.root == null)
{
this.root = n;
}
else {
var curr = this.root;
Que.push(curr);
}
while(Que.length>0)
{
curr = Que.shift();
if(curr.left != null && curr.right != null)
{
Que.push(curr.left);
Que.push(curr.right);
}
else if(curr.left == null )
{
curr.left = n;
break;
}
else if(curr.right == null)
{
curr.right = n;
break;
}
}
}
二叉树的遍历
层次遍历也采用队列思想:
function showLevel(node)
{
var queue = [];
var curr;
if(this.root != null)
{
queue.push(this.root)
}
while(queue.length>0)
{
curr = queue.shift();
console.info(curr.element)
if(curr.left != null && curr.right != null)
{
queue.push(curr.left);
queue.push(curr.right);
}
else if(curr.left == null )
{
continue;
}
else if(curr.right == null)
{
queue.push(curr.left);
continue;
}
}
}
执行结果:

先序遍历:
function showTree(node){
if(!(node == null))
{
node.show();
showTree(node.left);
showTree(node.right);
}
}
运行结果:

完整代码:
function Node(ele, left, right){
this.element = ele;
this.left = left;
this.right = right;
this.show = show;
}
function show(){
console.log(this.element);
}
function BinaryTree(){
this.root = null;
this.addNode = addNode;
this.showTree = showTree;
this.showLevel = showLevel;
}
function addNode(ele){
var n = new Node(ele, null, null);
var Que = [];
if(this.root == null)
{
this.root = n;
}
else {
var curr = this.root;
Que.push(curr);
}
while(Que.length>0)
{
curr = Que.shift();
if(curr.left != null && curr.right != null)
{
Que.push(curr.left);
Que.push(curr.right);
}
else if(curr.left == null )
{
curr.left = n;
break;
}
else if(curr.right == null)
{
curr.right = n;
break;
}
}
}
function showTree(node){
if(!(node == null))
{
node.show();
showTree(node.left);
showTree(node.right);
}
}
function showLevel(node)
{
var queue = [];
var curr;
if(this.root != null)
{
queue.push(this.root)
}
while(queue.length>0)
{
curr = queue.shift();
console.info(curr.element)
if(curr.left != null && curr.right != null)
{
queue.push(curr.left);
queue.push(curr.right);
}
else if(curr.left == null )
{
continue;
}
else if(curr.right == null)
{
queue.push(curr.left);
continue;
}
}
}
var Tree = new BinaryTree();
Tree.addNode(1)
Tree.addNode(2)
Tree.addNode(3)
Tree.addNode(4)
Tree.addNode(5)
Tree.addNode(6)
Tree.addNode(7)
showTree(Tree.root)
Tree.showLevel(Tree.root)
这样,我们就构建了一个二叉树:
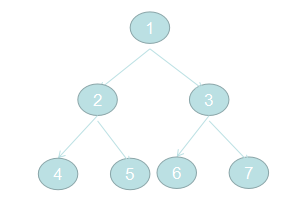
【js数据结构】可逐次添加叶子的二叉树(非最优二叉树)的更多相关文章
- Data Structure 之 最优二叉树
给定n个权值作为n的叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman tree).哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近. ...
- 树和二叉树->最优二叉树
文字描述 结点的路径长度 从树中一个结点到另一个结点之间的分支构成这两个结点之间的路径,路径上的分支数目称作路径长度. 树的路径长度 从树根到每一个结点的路径长度之和叫树的路径长度. 结点的带权路径长 ...
- 数据结构(3) 第三天 栈的应用:就近匹配/中缀表达式转后缀表达式 、树/二叉树的概念、二叉树的递归与非递归遍历(DLR LDR LRD)、递归求叶子节点数目/二叉树高度/二叉树拷贝和释放
01 上节课回顾 受限的线性表 栈和队列的链式存储其实就是链表 但是不能任意操作 所以叫受限的线性表 02 栈的应用_就近匹配 案例1就近匹配: #include <stdio.h> in ...
- JS数据结构第五篇 --- 二叉树和二叉查找树
一.二叉树的基本概念 从逻辑结构角度来看,前面说的链表.栈.队列都是线性结构:而今天要了解的“二叉树”属于树形结构. 1.1 多叉树的基本概念,以上图中“多叉树”为例说明 节点:多叉树中的每一个点都叫 ...
- 数据结构之Huffman树与最优二叉树
最近在翻炒一些关于树的知识,发现一个比较有意思的二叉树,huffman树,对应到离散数学中的一种名为最优二叉树的路径结构,而Huffman的主要作用,最终可以归结到一种名为huffman编码的编码方式 ...
- JS数据结构第三篇---双向链表和循环链表之约瑟夫问题
一.双向链表 在上文<JS数据结构第二篇---链表>中描述的是单向链表.单向链表是指每个节点都存有指向下一个节点的地址,双向链表则是在单向链表的基础上,给每个节点增加一个指向上一个节点的地 ...
- JS数据结构之 Map
JS数据结构之 Map Map介绍 Map(映射)是ES6引入的一种数据结构.这是一种存储键值对列表很方便的方法,类似于其他编程语言的哈希表. HashMap(哈希表),也叫做散列表.是根据关键码值 ...
- js对select动态添加和删除OPTION
<select id="ddlResourceType" onchange="getvalue(this)"> </select> 动态 ...
- JS对select动态添加options操作[IE&FireFox兼容]
<select id="ddlResourceType" onchange="getvalue(this)"> </select> 动态 ...
随机推荐
- 【转】Spring源码编译
原文地址: http://www.flyoung.me/2013/08/02/springcodecompile/ 参考资料: https://github.com/spring-projects/s ...
- 在Eclipse上通过插件获取github上的spring源码
spring源码开始的时候是通过SVN来管理代码的,后来是转移到github上管理源码的,可以通过在github上直接下载spring的源码. 下面讲解如何通过在eclipse上的插件git来获取sp ...
- 每天一个linux命令(32)--/etc/group文件详解
Linux /etc/group 文件与 /etc/passwd 和/etc/shadow 文件都是有关于系统管理员对用户和用户组管理时相关的文件.Linux /etc/group 文件是有关于系统管 ...
- Java基础之路(一)下--引用数据类型之数组
上次我们说了java的基础数据类型,今天我们就来说一下引用数据类型中的数组. 什么是数组 数组:存储在一个连续的内存块中的相同数据类型(引用数据类型)的元素集合. 数组中的每一个数据称之为数组元素,数 ...
- bash之管线命令
命令的输出需要经过好几道手续才能得到我们想要的格式,需要用到管线(pipe),(|) 管线命令(|)仅能处理stdandard output,对stdandard error output会忽略 管线 ...
- Jmeter+Badboy实战经验二(使用jmeter)
1. 新建线程组: TestPlan--添加--Threads(Users)--线程组
- AR入门系列-05-Vuforia识别目标视频播放
在识别目标后播放视频我们需要一个插件 Easy Movie Texture 2.36.unitypackage 百度网盘下载地址:http://pan.baidu.com/s/1skT8Xp7 将Ea ...
- 设置查询对话框的F7
1.定义自己的处理类public class MyQueryProcessor extends FMDefaultQueryProcessor { @Override public void proc ...
- wemall app商城源码Android之ListView异步加载网络图片(优化缓存机制)
wemall-mobile是基于WeMall的android app商城,只需要在原商城目录下上传接口文件即可完成服务端的配置,客户端可定制修改.本文分享wemall app商城源码Android之L ...
- 2761: [JLOI2011]不重复数字(平衡树)
2761: [JLOI2011]不重复数字 Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 2133 Solved: 825[Submit][Stat ...
